抓住定义，把握性质——圆锥曲线理解中的典型错误剖析

单建军 钱 慧

圆锥曲线是高考考查的重点和难点内容之一．题目通常以计算量大，综合能力强著称．对于同学们而言，解题时基本概念和性质理解的偏差，往往会导致满盘皆输，我们可以从以下几个方面加以归纳和总结．

一、对圆锥曲线的定义的理解

例1已知定点F1（－1，0），F2（1，0），动点P到F1，F2的距离之和为2，则点P的轨迹是________．

错解由椭圆的定义P的轨迹是椭圆．

错因剖析对于椭圆的定义把握不准．椭圆定义要求动点到两个定点的距离之和要大于两个定点之间的距离．而本题中PF1＋PF2＝F1F2，从而不符合椭圆的定义．

正解结合数轴，P的轨迹是线段y＝0（－1≤x≤1）．

例2已知定点F1（－1，0），F2（1，0），动点P满足，则点P的轨迹是________．

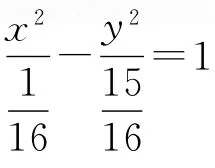
错因剖析对于双曲线的定义理解不透彻．双曲线的定义要求动点到两个定点的距离之差的绝对值为定长．而本题没有绝对值，故应该是双曲线的右半支．

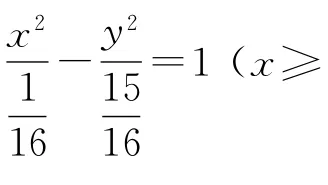
例3已知动点P到（0，0）的距离与点P到y轴的距离相等，则点P的轨迹是________．

错解由抛物线的定义知，轨迹是抛物线．

错因剖析对于抛物线的定义理解不准确．抛物线的定义中要求动点到定点的距离与它到定直线的距离相等，其中定点不在定直线上是问题的关键．

正解P的轨迹是直线y＝0．

在问题的处理过程中一定要理解定义的每一句话，尤其是几个注意点，比如椭圆要求动点到两个定点的距离之和要大于两个定点的距离，双曲线的定义中要求是距离之差的绝对值，抛物线要求定点不在定直线上等等．

二、对圆锥曲线的标准方程及其性质的理解

例4已知椭圆的离心率，则m＝________．

错解因为所以m＝3．

错因剖析对于椭圆的标准方程的理解有偏差，本题椭圆的方程不一定是焦点在x轴上的标准方程，故还需要考虑焦点在y轴上的椭圆的情形．

正解（1）当焦点在x轴上时，因为，所以m＝3．

（2）当焦点在y轴上时，因为，所以

综上：m＝3或

例5已知双曲线的渐近线方程为，则双曲线的离心率为________．

错解因为渐近线方程为所以，故离心率

错因剖析对于双曲线的性质理解不透彻，其中渐近线方程要区分焦点在x轴上还是y轴上．焦点在x轴上时，渐近线方程为，焦点在y轴上时，渐近线方程为．

正确解答（1）焦点在x轴上时，因为渐近线方程为，所以，故离心率

（2）焦点在y轴上时，因为渐近线方程为，所以，故离心率

例6抛物线的焦点坐标是________．

错解由抛物线的标准方程可知，焦点坐标为

错因剖析对于抛物线的标准方程和性质认识不到位．标准方程的形式应该是x2＝2py，焦点坐标是

正解抛物线的标准方程为x2＝4y，从而2p＝4，所以焦点坐标为（0，1）．

处理问题的过程中一定要熟练掌握圆锥曲线的几种形式的标准方程及它们的性质，注意区分椭圆以及双曲线焦点分别在x轴，y轴上的异同点，注意区分几种形式的抛物线的标准方程以及其性质的异同点．

在我们平时的学习过程中一定要抓住问题的实质，注意易错点，加强训练，逐渐提高分析问题和解决问题的能力．同时要注意提高处理问题的严谨性，才不至于“差之毫厘，谬以千里”．