函数零点与渐近线的关系浅探

要想寻找函数零点就需要用到渐近线,在早些年的高中数学教材里,渐近线是以简单要求出现的；近十几年,新课标教材为减少课业负担,把这一内容删除了。然而我们在日常的数学习题训练中发现,渐近线却是时常出现的。

一、司空见惯的渐近线概念

图1

在高一数学中,有一个函数由于图像存在渐近线而显得很重要,它就是双钩函数,即其中ab≠0。它有两条渐近线,即y轴直线和方程为y=ax的直线。

图2

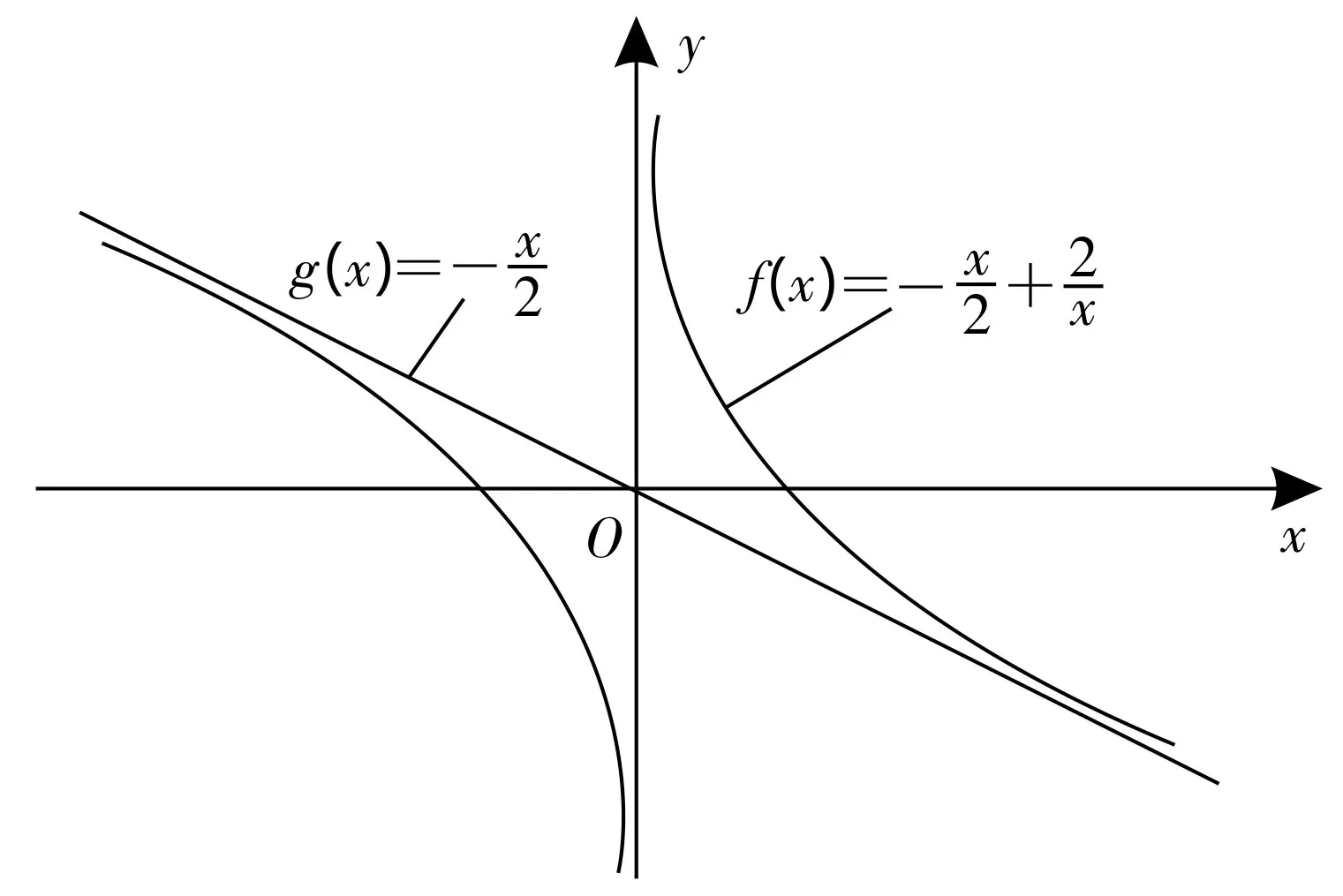
图3

二、渐近线总是伴随着图像变换

倒数变换是常见的图像变换,在倒数变换中,渐近线是伴随品,要认识变换后的图像性质,必须重视相应的渐近线存在。同学们在研究下面的四个例子时,也请注意原函数的零点或者趋向于无穷大的情况在倒数变换后的作用与变化。

1.从f(x)=x2+x+1到f(x)=,如图4所示,其中,x轴是渐近线。

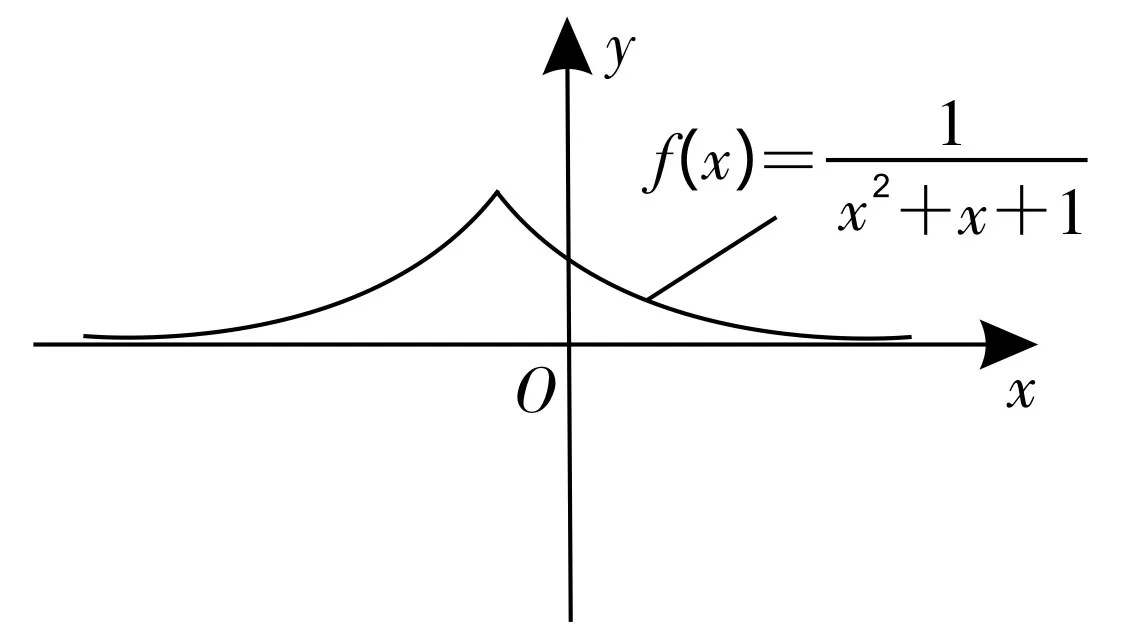
图4

2.从f(x)=到如图5所示,其中,直线x轴与直线是渐近线。

图5

3.从f(x)=x2+x-2到f(x)=,如图6所示,其中,直线x轴与直线x=-2、x=1等三条直线都是渐近线。

图6

4.从f(x)=lnx到,如图7所示,其中,x轴、x=1两条直线是渐近线,原点是空点。

另外,对渐近线的分类,人们习惯从它与x轴的相对关系角度去看待,可以分成三类：(1)水平的渐近线；(2)铅直的渐近线；(3)斜渐近线。

图7

三、总结

有了倒数变换的这一基础知识后,碰到一些分母含有变量分子为常数的函数,我们就可以考虑从分母这个基础函数出发,进行倒数图像变换,达到认识目标函数的目的了。

在图像的倒数变换时,即分子是常数且分母是含有变量的函数,或可以化成这样的函数,需要重视原来函数的零点和函数值趋向于无穷大的情况,它们都能产生渐近线,这些渐近线对我们画出陌生函数的图像,认识其性质,进而解决问题都有很大用处。