你想不到的数学（一）——生活中的函数图象

王成功

一看到婀娜多姿、形态万千的喷泉，我们的脑海里就会浮现出数学中的一条条抛物线，喷泉喷出的一条条优美的水柱就是通过电流改变水压，使得水流在水压的作用下，喷射出一条条抛物线．

抛物线同样也应用于高台跳水运动，跳水运动员在空中的跳水轨迹呈抛物线，需要根据跳水的速度和二次函数的性质，计算出在空中可以做动作的时间，这样才能使运动员在跳水过程中有一个完美的运动弧线和精彩的表演动作．

其实函数曲线在实际生活中的应用远远不止这些，随处可见．

享有世界第一大斜拉桥盛誉的中国苏通大桥，它是世界上规模最大、技术难度最高的斜拉桥，主跨度达1088m的双塔斜拉桥，整个桥是由两个主A型主桥墩，两侧用数十条斜拉钢索连接而成，整个桥的设计，充分运用了力学原理，桥身设计以及斜拉钢索的设计，融入了函数曲线，尽显抽象的美感，令世人震撼．

生活中，如刀削面机器人，其工作原理就是一个简单的周期函数．在工作中，把机器人手臂的摆动曲线定义成一个周期函数，再设定好每个周期t的一个固定值，这样就可以进行自动削面了．

同样在医学上，心电图、核磁共振等医学机器的使用也是函数原理和函数曲线的直接应用．例如核磁共振，通过检查人的脑电波，形成核磁共振谱和红外光谱，医生通过分析光谱曲线，从而确定病人的病因．

现代临床高场（3．0T）MRI扫描

在初等数学中研究的函数都是基本初等函数模型，其图象也很简单．为了让函数更好地应用于生活，服务于我们的生活，可以把简单的函数及曲线进行拓展和复合，二维的函数拓展到三维空间或五维空间．

如右图所示的图形，是通过先建立极坐标系，定义一个含参数t的函数r＝4cos（ct），然后画出函数图象得到的，你千万不要认为是空间图形，其实它是一个地地道道的平面图形．

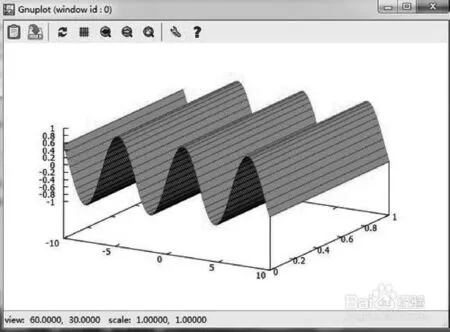
下面的空间美图是把某函数的图象，沿着纵向伸展开，即把曲线从平面内拓展到空间而形成的，从而实现从二维空间到三维空间的转换．

把基本的初等函数图象延伸至五维空间，这个过程必须借助于计算机来实现，正是通过计算机技术结合函数、参数设置从而可以电子模拟出多维空间的函数图象，通过这些多维函数图象，可以设计出全方位服务于我们生活的物品来．

形状和轮胎一样的图形，往往不是一个函数和一个坐标系所能解决的，这需要同时建立2～3个坐标系，并借助于软件命令对所画图形进行着色才能达到预想的效果．当然无论多么复杂的图形，我们都可以对其建立适当的坐标系，对复杂图形进行分解，从而通过基本初等函数的图象来解决．

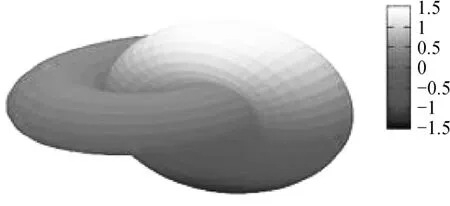
美轮美奂的函数图象正在悄无声息地进入我们的视野，数学正在潜移默化地改变着我们的生活，只有留心我们的生活环境，才能真切感受到函数离我们那么近，也只有这样才能激发我们学习的欲望和提升我们学习函数的兴趣．