小折纸，大文章——折出问题的答案

常文武

平面几何是一门较难的学问，因为一题一个解法，且辅助线不易想到．下面就是一些有一定难度的问题，我们看看如何另辟蹊径，尝试用折纸法探求解题思路．

题目一

如图1，已知等腰直角三角形△ABC以及经过直角顶点A的直线EF．如果BE∥CF，求证：AE2＋AF2＝BE2＋CF2．

分析此题目，与证明有关联的4个量似乎离得比较远，尤其EB和FC这两条线段．再来看结论像是和勾股定理有关系，但是图中并没有含这些边的直角三角形．所以我们知道此题不添辅助线是断难解出的．

但是如果我们用折纸来找思路，可以绕开辅助线，直捣黄龙！

将图1打印在纸上，剪下来把玩一番（打印机不凑手，可以画一个图来剪）．

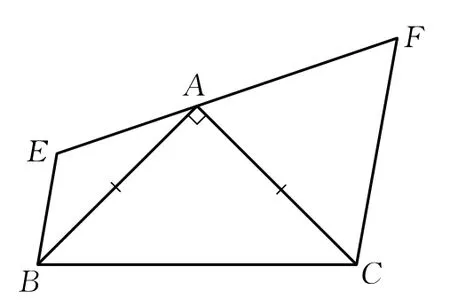
图1

通过折叠我们容易发现，可以让BE，EA，AF，FC这四条边“聚首”：将AB折到AC上，同时外翻AB，AC成山折．结果如图2．

通过这些折纸的操作，原来的三角形ABC不见了，出现了一个新的四边形AFCE．所证的结论转化为证明 ∠EAF＝∠ECF＝90°．这个是不难证明的．证明留给读者了！无独有偶，我们再看一题．

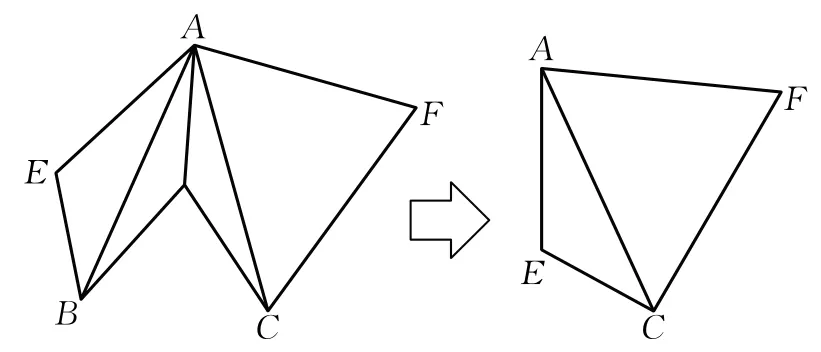
图2

题目二

如图3，△ABC中，M是BC中点，ME⊥MF，且ME＝MF．求证：AE2＋EB2＝AF2＋FC2．

如同第一题一样，需要构造直角方能利用勾股定理．故技重施，打印图形来把玩一番吧！结果发现，如果照下面四步折，问题的答案就浮出水面了．

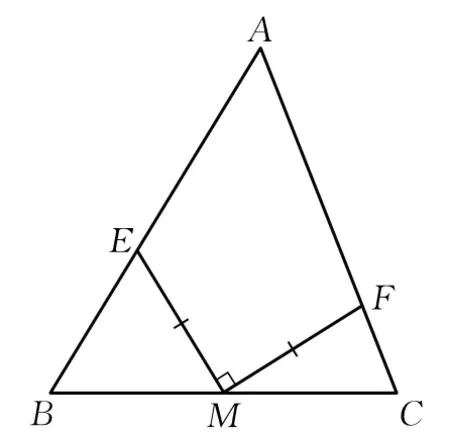
图3

1．过EF折一道山线，将角A折到后面．

2．过EM折一道谷线．

3．过MF折一道谷线．这时角B和角C翻折后会合为一点（为何能会合？）．

4．将纸片翻过来．

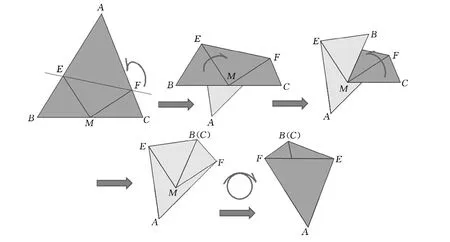
图4

现在，我们从图4的示意中看到结果是一个四边形，并且有两个相对的角是直角．于是和第一题一样，问题迎刃而解了！证明过程留给读者．

题目三

已知△ABC中，∠A＝100°，∠C＝30°，在AC上截取AD＝AB，连结BD．求证：BD＝AC．

同上题一样，貌似简单的题目一碰即知其难啃的本质．不过当纸片在手，任人“折磨”的时候，难题不免要低头了．怎么折呢？常规思路是把两条要证明相等的线段化到一起去比较．所以最自然的想法是折出∠ABD的角平分线将AB（长度等于AD）搬到BD上；同时，折出∠CDB的角平分线，将CD搬到DB上，结果发现如图6的现象．

图5

图6

实验不但佐证了结论，也给了我们进一步探寻的方向：两个折起的角碰到一起的地方有什么讲究？

打开纸片，折底边中垂线，发现折痕刚好经过会合点．

图7

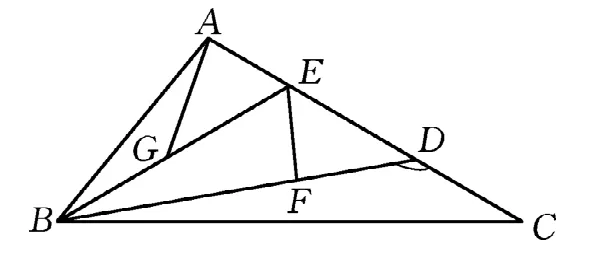
图8

最终，我们尝试发现有三个全等的等腰三角形（△ABG，△FBG，△CFD），如图8所示那样嵌入到三角形ABC中．BD边上放置了底边和一腰，而AC＝AD＋DC正好也等于该等腰三角形的底边和一腰．至此问题全部解决．

简证：在AB边上向内作等腰三角形ABG，使得∠ABG＝∠GAB＝20°．沿着BG翻折△ABG得到△FBG，则F在BD上（为什么？）．同时折痕BE交AC于E．

连结EF，易证 ∠AEB＝∠BEF＝60°．所以EF平分角∠BEC．又∠EBC＝∠C＝30°，故EF是等腰△BEC的对称轴．沿着EF翻折△BGF得到△CDF．至此通过翻折两次我们得到了三个全等的等腰三角形．剩下的就是简单的算术题了．

题目四

如图9，在△ABC中，∠A＝20°，AB＝AC，∠BCD＝50°，∠CBE＝60°．求证：∠BED＝30°．

此题看似友善，但却是名副其实的难题，在网上流传甚广．有人用角格点来归类，用正弦定理来求解．也有的人添正三角形辅助线来求解．无论如何过程和方法都不简单．

然而，如果用折纸来探寻解题思路，就会有如庖丁解牛般“秒杀”．

步骤：

基于三黄泻心汤的黄芩-大黄-黄连不同剂量配伍对黄芩苷和汉黄芩苷溶出的影响 ……………………… 邓丽红等（3）：334

1．打印这个图，剪下备用．

2．试着找找纸片的形状中隐藏的等量关系．不经意间你会发现BC＝BD．发现这个相等量只要折出∠ABC的角平分线便可发现C，D重合（当然，证明也很简单）．如图10．

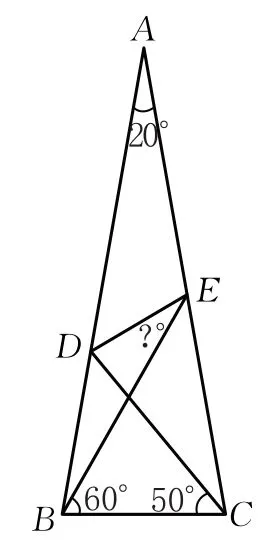
图9

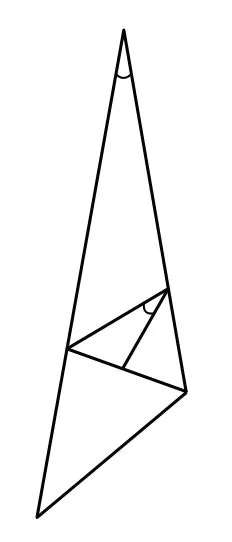
图10

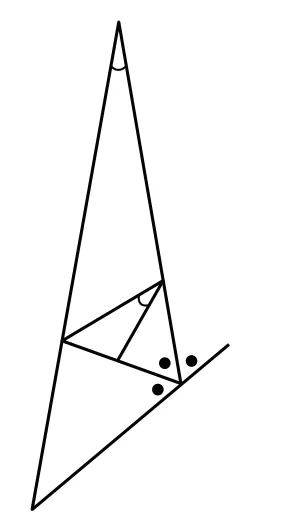
图11

3．这时，敏锐的观察者会有一个发现：如图11所示，这里有了三个60°角（为什么）！

4．惊喜之余，好事连连！通过翻折发现原图中的DE在图13中也是∠ADF的角平分线！

图12

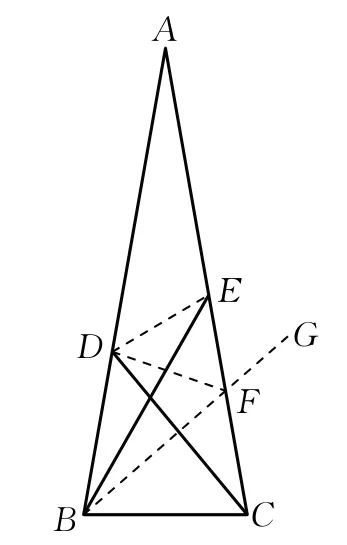
图13

5．现在的思路形成了——如果观察属实，所有问题就迎刃而解：∠ADE＝50°，∠ABE＝20°，所证成立．可是第4步发现的角分线如何证明呢？

6．打开所有折痕，还有一个发现，BE是第一道折痕与BD的夹角的角平分线．

已知若干个角平分线，要证一条线也是角平分线．如此多的角平分线强烈暗示我们，要用三角形旁切圆性质．

简证：点E是△BDF的∠DBF的角平分线上的点，也是外角∠DFG角平分线上的点，所以它一定也在另一外角∠ADF的角平分线上．即得证．

上述4道题，借助折纸可以帮助我们探明解题的方向，甚至直接得出题目的解．真是“小小纸张，变化万方”！同时也告诉我们，平时解题时，不妨胆子大一些，多尝试，细分析，说不定就会有所收获．

特别提醒：数学解题是严谨的，找到了方法，还必须用规范的数学语言将其严格证明出来，本文的论述只是解题思路的展示，严格的证明就请同学们自己写一写．