从类比的角度探究正多面体的对偶现象

张竞择

2018年高考结束后，我看到江苏卷第10题是一道立体几何问题：

如图1所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．

让我感兴趣的是，正方体各个面的中心恰好构成一个正八面体（每个面都是正三角形，如图1），这其中有着什么样的规律呢？于是借助于网络检索和动态几何软件（几何图霸），我展开了一番探求．

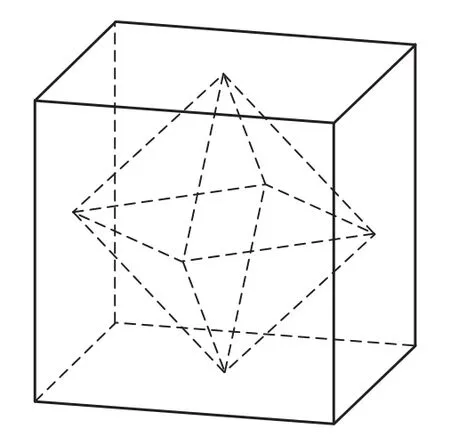
图1

一、正多面体的构图

正多面体，或称柏拉图立体，指各个面都是全等的正多边形且每一个顶点所接的面数都一样的凸多面体．研究一个数学内容首先需要画出它的内容，正如有图有真相，而绘制正多面体的图形，是我研究过程中面对的第一道坎．以正八面体为例，如果不是如图1一样构造，而是单独画出来，应该怎么操作？

在多次尝试未果的情形下，突然想到：平面几何中正多边形通常可以在外接圆的背景下构造，如图2，⊙O中先构造AB边（基本图形），然后将弦AB绕着圆心O旋转60°得到第二条边，……如此旋转5次可得到正六边形；同理，正多面体也是可以借助于外接球来实现的，如图3，在球O中构造等边△ABC（基本图形），然后将△ABC绕着轴OA旋转90°后得到△ACE，……当然立体图形要较平面图形复杂，除了旋转外，还有对称，即△DCB与△ACB关于面OBC对称，这样通过旋转和对称，可由基本图形得到正八面体ABCDEF．

图2

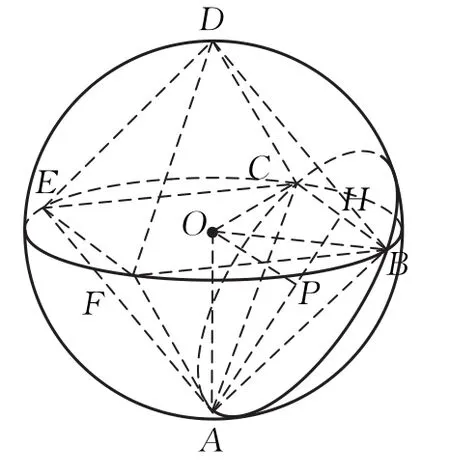
图3

在上述构造中，从平面到立体其实是一种类比的思维方式，具体而言：正多边形→正多面体，外接圆→外接球，线段AB→等边三角形ABC，绕点O旋转→绕轴OA旋转……事实上，基本图形的构造，也充斥着类比的影子，图2中，先构造线段，再作弦AB⊥OP；图3中，过P作垂直于OP的球的截面圆，在圆P上任取一点A，将A绕P分别旋转120°、240°后得到点B、C，这样可以构造出等边三角形ABC．

二、正多面体的种类

解决一个陌生问题时，我们可以借助类比，从熟悉并相关的问题中寻找到解题思路．当然并不是所有的问题都可以类比的，如我们知道正多边形有无数种，但这个结论却不能类比到正多面体中，其实我也是经过多次碰壁，用百度搜索后才知道正多面体仅有五种，即正四面体、正六面体、正八面体、正十二面体、正二十面体，而且这个问题居然早在古希腊时代就已被柏拉图所解决．证明仅有五种正多面体的方法大致有以下两种：

设正多面体由y个正x边形围成，任意一顶点出发有z个正x边形，且x≥3，y≥3，z≥3．

方法一：正x边形每一个顶角为

又多面体在一个顶点处多面角的平面角小于360°，

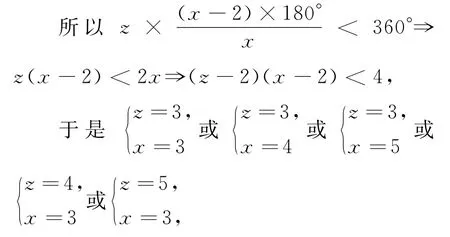
从而说明正多面体仅有五种．

代入欧拉公式：多面体的顶点数V、棱数E、面数F满足关系式V＋F－E＝2，

说明：（*）式是一含有三个未知数的不定方程，我采取的策略是先控制x的范围，然后再通过讨论得到有限组解．

三、正多面体的对偶现象

我们知道，连接正n边形各边的中点可以得到另一n边形；类似的，连接正多面体每个面的中心可以得到一新的正多面体，这是一有趣的对偶现象．

事实上，观察前面的五组解可以发现：正六面体的顶点数、面数与正八面体面数、顶点数对应相等（如图1，顶面互换、棱数不变），正十二面体的顶点数、面数与正二十面体面数、顶点数对应相等（如图5）．事实上，以正六面体为例，取每个面的中心，如果两个面有邻边，则连接两个面的中心，否则两点之间不连线，所有中心和连线构成的空间图形为正八面体；于是，正八面体每个面的中心连线构成正六面体；正十二面体每个面的中心连线构成正二十面体，而正四面体每个面的中心连线还是正四面体（如图4）．

图4

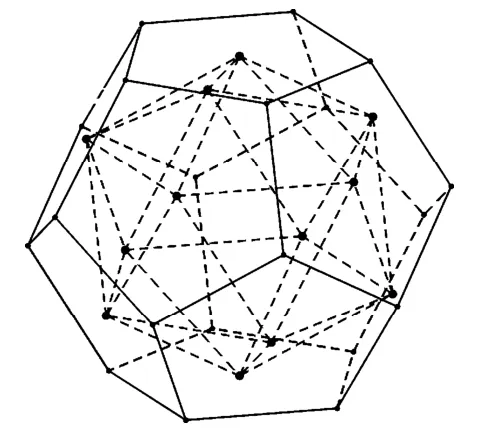
图5

这样，同学们一定可以发现，江苏高考卷第10题的背景其实就是正多面体的对偶现象．通过一道高考题的挖掘，借助于网络，我们学到了很多知识，如欧拉公式、正多面体等，当然还有很多问题值得我们进一步探索，如正十二面体的外接球、内切球的半径的求法，又如网上文章提到的对称群、欧拉示性数、曲面三角剖分等，我都不是很明白，但通过这一次探究，让我对“处处留心皆学问，人情练达即文章”有了更多的领悟，相信这些问题会在不久的将来迎刃而解．

（编者注：关于正多面体及其对偶体的更多美妙图形和性质，请参见《数学文化素质教育资源库》之《数学之美》）