四招突破圆锥曲线离心率问题

李连兴

离心率是联结圆锥曲线的多种几何性质的“核按钮”，是高考考查的热点．求圆锥曲线的离心率有以下四种常见方法．

一、直接解出基本量

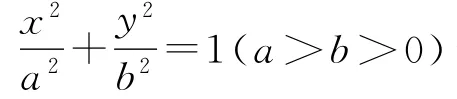
解（1）由题设知，a2＝b2＋c2，e＝，由点（1，e）在椭圆上，得

评注这类题一般都能够根据已知条件直接解出a，c，从而求得e．

二、从圆锥曲线定义出发

例2已知点P是双曲线上一点，F1，F2分别是双曲线的左、右焦点，且|PF1|＝e|PF2|，则该双曲线的离心率e的取值范围为________．

解析很多同学感到疑惑的是，题目中看不出有明显的能形成不等关系的量．我们看到有条件|PF1|＝e|PF2|．可以尝试用双曲线的定义进行转化．

由双曲线的定义知|PF1|－|PF2|＝2a，

此时，我们要用到一个关于双曲线的比较重要的结论：|PF2|≥c－a．（可以画个草图，作出与F2相应的准线，则|PF2|的大小与P到准线的距离成正比）

评注双曲线上的点到同侧焦点的距离的最小值是在顶点处取到的，这个结论看似简单，实则非常重要，建立不等关系后，用到了二次不等式的知识，本文的第四部分会重点介绍建立齐次方程求解离心率的方法．

三、从图形特征入手

这类问题要画出图形并研究图形的几何特征．要将图形的几何特征分析清楚以便找出a，b，c的关系．如果几何特征不能看清，则可能带来繁琐的计算．

例3在平面直角坐标系中，已知椭圆，以O为圆心，a为半径的圆，过点P作圆的两切线互相垂直，则离心率e＝________．

解析如图1，切线PA，PB互相垂直，又OA⊥PA，OB⊥PB，所以四边形OAPB是正方形，进而△OAP是等腰直角三角形，故，解得

图1

点评此类题目应通过画图分析几何特征，注意圆、等边三角形、菱形、正方形等特殊图形中所蕴含的数量关系，找到解题突破口．

四、从代数方程突破

此类题目通常要根据条件（尤其要善于利用圆锥曲线的方程）列式，变形，最终得到关于a，c的齐次方程，解出，即e的值．

例4如图2，在平面直角坐标系xOy中，A1，A2，B1，B2为椭圆的四个顶点，F为其右焦点，直线A1B2与直线B1F相交于点T，线段OT与椭圆的交点M恰为线段OT的中点，则该椭圆的离心率为________．

图2

解析直线A1B2的方程为：；直线B1F的方程为：

点评本题的关键是要根据点M在椭圆上，求出点M的坐标，代入椭圆方程，得到关于a，c的齐次方程，进而求出离心率．本题的解法思路代表一类求离心率问题，具有一般性，要认真体会，触类旁通．

综上，求离心率的四种方法，其实质是利用所给条件，结合图形的几何特征，列出关于a，c的方程或不等式（组），进而求出离心率或其取值范围，体现了解析几何处理问题的基本思想方法．可以说，四法归一，数形结合．