过圆锥曲线准线上一点的切割线性质
2019-07-08 10:27江西省赣州市第一中学341000
中学数学研究(江西) 2019年6期
江西省赣州市第一中学 (341000)
宁荣富
笔者在研究过圆锥曲线准线上一点的切割线时,发现它们具有一个统一性质,现将结论展示如下.


图1
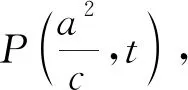


连结PF交椭圆C于点D、E,过A、B分别作准线l的垂线AA′、BB′,垂足为A′、B′.

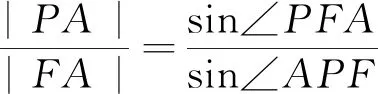
由②、③、④得sin∠PFA=sin∠PFB,而∠PFA<∠PFB,故∠PFA=π-∠PFB,也即∠PFA=∠EFB,∴∠T1FA=∠T1FB,命题1成立.
类比上述方法可证明双曲线的情形,即有下列命题成立.


图2
命题3 已知P是抛物线C:y2=2px(p>0)准线l上一点,抛物线焦的点为F,过点P作抛物线C的两条切线和一条割线,切点为T1、T2,交点分别为A、B.则有(1)PF⊥T1T2;(2)T1T2平分∠AFB.

图3


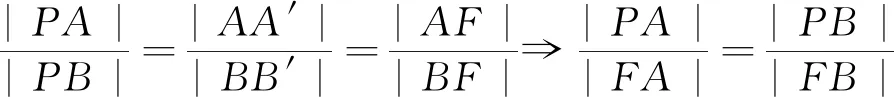
由⑤、⑥、⑦及∠PFA<∠PFB,得∠PFA=π-∠PFB,∴∠PFA=∠EFB,即∠T1FA=∠T1FB,命题3成立.
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08
中学数学研究(江西)(2021年8期)2021-09-06
中学生数理化(高中版.高考数学)(2020年12期)2021-01-13
中等数学(2018年7期)2018-11-10
物理教学探讨(2017年10期)2017-11-15
中学生理科应试(2016年10期)2016-12-06
福建中学数学(2016年8期)2016-12-03
福建中学数学(2016年4期)2016-10-19
福建中学数学(2013年1期)2013-03-06
数理化学习·高一二版(2009年2期)2009-03-30

