让学生的思维飞起来
——基于新课改背景下高中数学解题思维培养浅析
浙江省杭州市富阳区新登中学 (311404)
于德强
我们在解决数学问题时,常常会遇到很难的题目,按照常规的思考方法可以解答,但要花费大量的时间,在限时完成的考试中不适用.一种选择就是放弃,因为难题往往是在每种题型的最后部分出现;另一种就是把平时积累的思维方法提升,站在更高的角度看问题,让思维飞起来,从而解决问题.要做到既快速又准确,需要长时间的训练,也要养成良好的解题习惯.
不拘泥于问题的形式,而是细致分析问题的结构特征,从意想不到的角度去思考问题,从而达到解决问题的目的与效果,这样的思维方式既培养了良好的解题习惯,又开拓了学生视野与见识,让人智慧得到锻炼与进步.这样的数学问题在近年来的高考或模拟卷中经常出现.
一、抓住内在联系,让思维飞起来
1.原题呈现

图1
例1 如图1,正四面体ABCD的棱CD在平面α上,E为棱BC的中点.当正四面体ABCD绕CD旋转时,直线AE与平面α所成最大角的正弦值为.
1.1 命题背景:本试题考察立体几何中的线面角,通过几何图形为背景给定已知条件,要求空间角的最大值.
1.2 难度分析:从已知条件可知,正四面体ABCD的棱CD在平面α上,整个几何体旋转,导致直线AE与平面α的交点位置随之变化,斜线(长)、垂线(长)都发生变化,甚至无法做出这个角的平面图,因此难度较大.
2.尝试解答

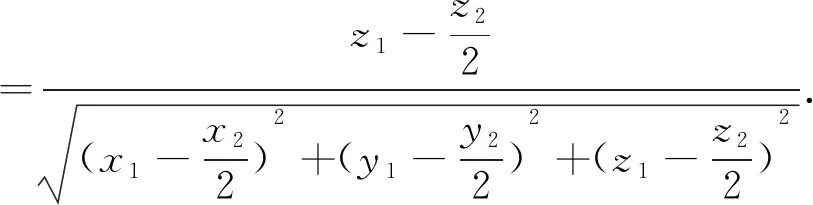
2.2 函数法:设点A到平面的距离为x,由于直线AE的射影不断变化,二者均呈变化趋势,无法建立有效的函数关系式,基本无法解决.
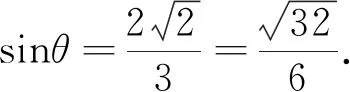
3.思维突破

图2
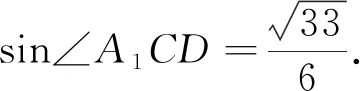
经过思维迁移,将问题转化为一个圆锥母线与轴截面成角最大的问题,相对于以上几种解法,思考方式难了一些,但是掌握了以后,可以使问题解决的更具创造性.
二、抓住变化规律,让思维飞起来
1.原题呈现
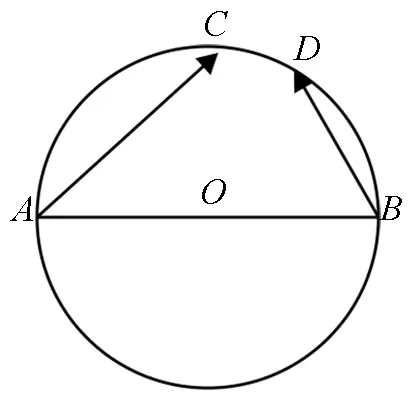
图3

1.1 命题背景:本试题考察平面向量的数量积,通过几何图形给定已知条件,去求两个不定向量的数量积.

2.尝试解答
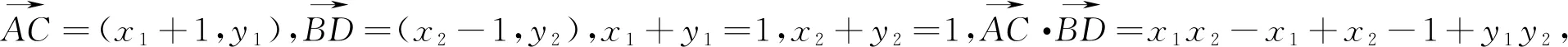
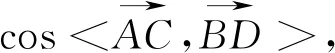

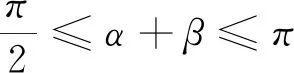

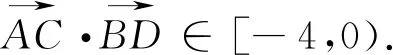
3.化动为静
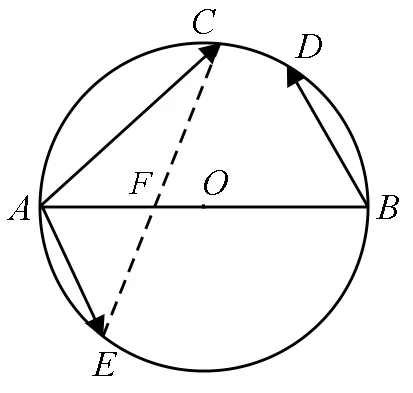
图4
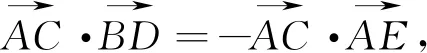
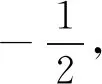
经过化动为静,将问题转化为一个应用基本不等式求一个目标函数的最值问题,相对于以上几种解法,思考方式更难,但运算量更小,放缩更自然.

三、抓住问题本质,让思维飞起来
面对较难的高中问题,使用常规方法即使可以解答,但所花精力实在太大.不能呈现高效课堂,不能以最小的投入使学生获得最大的收益.在某些特定的环境下,出奇制胜也很重要,如果经过细致分析,通过转换与化归,让思维飞起来,可以使解决问题的过程成为享受,从容面对高考的考验.同样的,对于各种不同背景的问题,也可采用一些方法抓住问题的本质,“他山之石,可以攻玉”让问题的解决变得相对容易,进而给学生的收益无限放大,培养学生思考问题,分析问题,解决问题的素养,提高学生解数学题的能力.
1.他山之石,可以攻玉

分析:初看本题,直觉就是进行三角变换,转化为某类三角函数求值域.但是考虑到分式的结构以及分子分母的联系,可利用向量进行转化,另辟它径,给予解决.
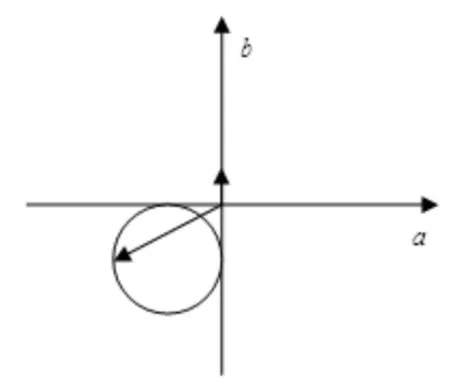
图5
解:已知函数f(x)=
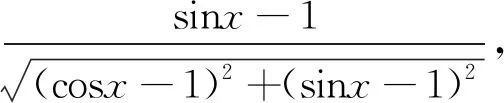
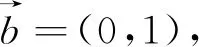

反思:充分发挥知识的横向联系,起到意想不到的效果,可谓是它山之石,可以为锉;它山之石,可以攻玉.
2.构造函数,巧妙解决
例4(2012年高考浙江理)设a>0,b>0.下列命题正确的是( ).
A.若2a+2a=2b+3b,则a>b
B.若2a+2a=2b+3b,则a C.若2a-2a=2b-3b,则a>b D.若2a-2a=2b-3b,则a 解:条件是一个等式结构,左右两边的系数有小的差异,消除差异,可得:若2a+2a=2b+3b,必有2a+2a>2b+2b.则可构造函数f(x)=2x+2x,因为f′(x)=2x·ln2+2>0恒成立,故有函数f(x)=2x+2x在x>0上单调递增,即a>b成立.其余选项可用同样方法排除. 反思:我们得到一个很有用的小经验:若一个等式(或不等式)两边结构形式相同(系数相同、仅字母不同),则可尝试去构造一个函数来解决问题. 3.透析本质,一步到位 例5已知a2sinθ+acosθ-2=0,b2sinθ+bcosθ-2=0(a,b,θ∈R)且a≠b,直线l过点A(a,a2),B(b,b2),则直线l被圆(x-cosθ)2+(y-sinθ)2=4,所截得的弦长为. 解:由已知抽象出直线l的方程为xcosθ+ysinθ-2=0,圆心到直线l的距离为 反思:直线被圆截得的弦长问题,关键在于直线l的方程是怎样的,摸清题意,从问题本源出发,才能迅速找到出路.得到直线方程是大多数学生可以想到的.问题在于快速得到是一件不太容易的事情.直线过两点,先求斜率,再利用已知条件,消去字母a,b,进而得解.这个感觉就是没有完全掌握题意,使一道填空题变成解答题了. 4.重视方法,手段精妙 A.∠ABC=90°B.∠BAC=90° C.AB=ACD.AC=BC 5.巧妙换元,化繁为简 巧法,着眼于提高,在于能整体的把握问题,巧妙的使用条件,是抽象、概括,发散及合情推理的产物.对待巧法要辩证的对待,既不轻视,又不能过多的运用. 解析:代数式求最值的题目很多,关键在于向哪个方向去转化,整体去看待问题,让分子分母的结构更简单最好,这样均值不等式就可一展身手. 反思:本题给定的代数式的结构与特征明显,含有两个字母参数,一般的解题方式是先通分,把分子分母化成相同的变量,构造函数或用均值不等式来解.但考虑到如果分母的形式更简单,那么解决起来会更容易.巧妙换元,将问题转化到均值不等式,达到目的. 转变1:实现由重知识向重发展的转变 通过再思考,让学生的思维方式转变,帮助学生掌握数学知识,又可培养学生解决实际应用问题的能力,这恰是新课标所提倡的基本理念.从这个意义上说,教学过程既是学生掌握知识的过程,又是一个身心发展、潜能开发的过程.当代新基础教育课程的教学应致力于发展学生包括智力在内的整个个性和整体素质的提高. 转变2:实现由重结果向重过程的转变 “重结果轻过程”,这是教学中一个十分突出的问题,就题讲题,忽视了对知识点的归纳,导致很多学生课后都不知道彼此的区别与联系.而深入思考能促使学生的学习方式由“重结论轻过程”向“过程与结果”并重的方向发展,使学生挖掘隐含问题的本质属性,从而达到“做一题,通一类,会一片”的解题境界. 总之,对数学难题的重点研究,教师设计的时间花得多一点,学生练习的时间就少一点;设计的例题精一点,学生就会学得活一点,好一点.虽然我们经常一节课只研究一个问题或一个题型,有时到下课了还没有研究结束,但这样的教学效果特别好,学生得到的是思想方法,是情感体验.数学解题不应是“自古华山一条道”,而应是“条条大路通罗马”,这样才能源于教材却又高于教材,这样的教学才能收到异曲同工之妙、殊途同归之效.试题的解法探究对一道填空题可以从多个维度去考量,利用不同的思想方法加以思考和探究,能探究出多种解法,从而实现一题多解的目的.一道好的试题,不在于华丽的“包装”,而在于本身所蕴涵的思想方法.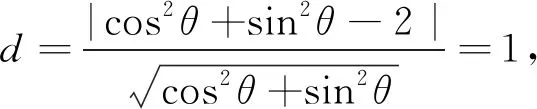

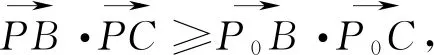

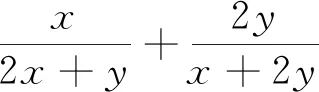

四、让思维飞起来意义深远

