对一个三点共线问题的进一步探究
2019-07-08 10:27湖南省浏阳市教育科学研究所410300
中学数学研究(江西) 2019年6期
湖南省浏阳市教育科学研究所 (410300)
朱保仓
湖南省浏阳市长郡浏阳实验学校 (410300)
李剖华
文[1]对圆锥曲线中三点共线问题的解题策略进行了研究,读后受益非浅,特别是其中的例2引起了笔者的思考与探究,现将笔者的心得体会与大家交流分享.

图1
引例(文[1]例2)如图1,已知曲线C:x2+2y2=8,设曲线C与y轴的交点为点A、B(点A位于点B的上方),直线y=kx+4与曲线C交于不同两点M、N,直线y=1与直线BM交于点G,求证:A、G、N三点共线.
问题题目中的结论是特定椭圆的特有性质吗?一般椭圆是否都有类似的性质呢?

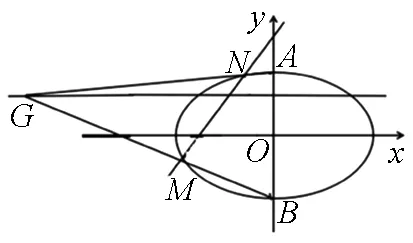
图2


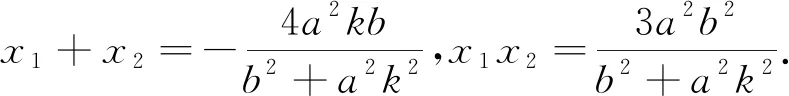

将①代入②知②成立,所以A、G、N三点共线.即猜想成立.
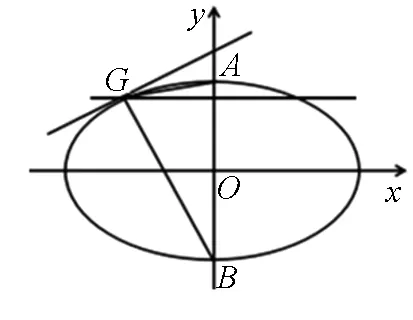
图3
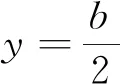
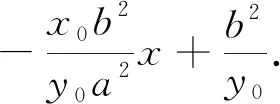

图4

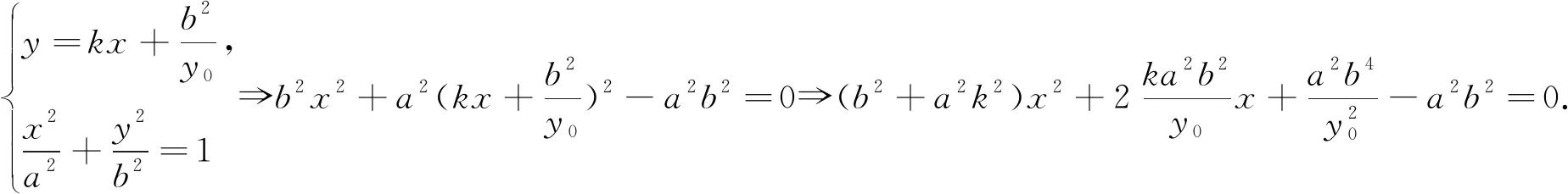




将①式代入易得③式成立,所以A、G、N三点共线.
探究3 将A、B换成长轴上的两点,是否会有类拟的结论呢?
通过探究,可以得到如下结论:
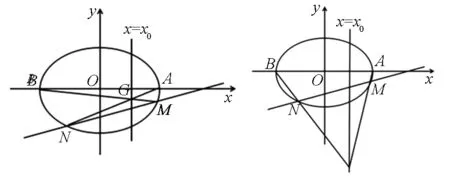
图5 图6
证明过程与猜想2的证明过程类似,在此不再赘述.
猜你喜欢
数学杂志(2022年5期)2022-12-02
猪业科学(2022年10期)2022-11-03
新高考·高一数学(2022年3期)2022-04-28
湘潮(上半月)(2021年11期)2022-01-15
文艺生活(艺术中国)(2021年8期)2021-09-18
中等数学(2021年4期)2021-08-14
中学生数理化·高一版(2021年5期)2021-07-21
中学生数理化(高中版.高二数学)(2021年12期)2021-04-26
新教育论坛(2019年14期)2019-09-10
福建中学数学(2016年4期)2016-10-19

