一道高中数学联赛预选题的再探究
福建省莆田第五中学 (351100) 吴雪琴
1.已有结论呈现
文【1】对2016年全国高中数学联赛湖南赛区预赛试题题13进行探究,得到了椭圆、双曲线、抛物线定点问题的几个结论,并由此综合得出圆锥曲线的一个定点性质,读后颇受启发,但觉意犹未尽.本文拟对上述结论进行推广.先把文【1】中的定理1,2,3抄录如下:
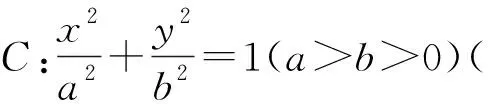

以上定理揭示了圆锥曲线的焦点与准线的一个关联性质,我们不禁要问:如果把定理中的“焦点”与“准线”分别换为“类焦点”与“类准线”,这一结论还成立吗?
2.探究结论的推广
经探究发现,以上定理的结论不仅对圆锥曲线的焦点与准线成立,对“类焦点”与“类准线”仍然成立.为此,下面把上述性质推广到“类焦点”与“类准线”的情形.

证明:分两种情况讨论.
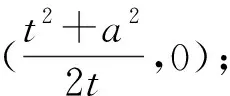
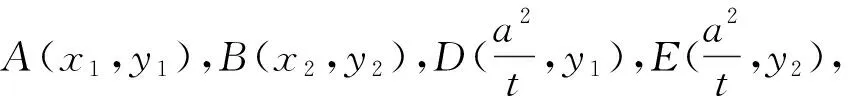

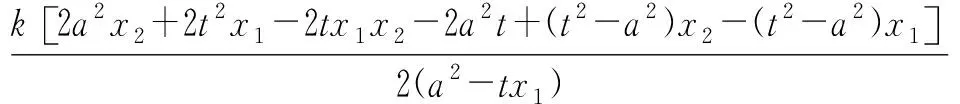

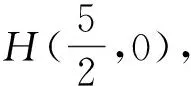
类似地,可把定理2,3分别推广为

定理3.1 设抛物线C:y2=2px(p>0),直线l经过抛物线C的“类焦点”F(t,0)(t>0),与抛物线C交于点A,B,点A,F,B在“类准线”x=-t上的射影依次为D,K,E,则对任意直线l,直线AE与BD相交于线段FK的中点(0,0).
下面只给出定理3.1的证明,定理2.1仿定理1.1可证.
证明:分两种情况讨论.
当直线l垂直于x轴时,显然有直线AE与BD相交于线段FK的中点(0,0);



定理4.1 设圆锥曲线C,直线l经过圆锥曲线C的“类焦点”F,与圆锥曲线C交于点A,B,点A,F,B在相应的“类准线”上的射影依次为D,K,E,则对任意直线l,直线AE与BD相交于线段FK的中点G.
3.推广结论的完善
上述推广的逆命题成立吗?即设点F在“类准线”上的射影为K,点D,E在“类准线”上,若对任意直线l,直线AE与BD相交于线段FK的中点G,那么点D,E是否为点A,B在“类准线”上的射影?
设点A,B在“类准线”上的射影为D1,E1,据定理4.1,得对任意直线l,直线AE1与BD1相交于线段FK的中点G.这表明直线AG经过点E1,又由直线AE与BD相交于线段FK的中点G,知直线AG经过点E,则点E,E1同为直线AG与“类准线”的交点,故点E,E1重合,从而点E为点B在“类准线”上的射影.同理可证点D为点A在“类准线”上的射影.可见定理4.1的逆命题成立,故定理4.1可完善为
定理4.2 设圆锥曲线C,直线l经过圆锥曲线C的“类焦点”F,与圆锥曲线C交于点A,B,点F在“类准线”上的射影为K,点D,E在“类准线”上,则对任意直线l,直线AE与BD相交于线段FK的中点G的充要条件是点D,E分别为点A,B在“类准线”上的射影.
由定理4.2,可把定理1.1、2.1、3.1分别完善为


定理3.2 设抛物线C:y2=2px(p>0),直线l经过抛物线C的“类焦点”F(t,0)(t>0),与抛物线C交于点A,B,点F在“类准线”上的射影为K,点D,E在“类准线”上,则对任意直线l,直线AE与BD相交于线段FK的中点(0,0)的充要条件是点D,E分别为点A,B在“类准线”上的射影.
至此,我们完成了对上述全国高中数学联赛湖南赛区预赛试题的再探究,推广和完善了文【1】的圆锥曲线定点问题的几个结论.
4.教学反思
著名数学教育家G波利亚说过:“没有任何一个题目是彻底完成了的,总还会有些事情可以做”,“好问题同某种蘑菇有些相像,它们都成堆地成长,找到一个以后,你应当在周围找一找,很可能附近有好几个”.竞赛、高考等各类试题是众多专家集体智慧的结晶,具有原创性和可探究性,这些试题是命题者留给我们的一笔宝贵“财富”,不应满足于会解和已有结论,引导学生对之进行适当探究,寻找“蘑菇”,使这些“财富”有所“增值”.这对培养学生的探究意识和探究能力,提升数学学科核心素养无疑是有益的.

