如何构造函数

戈 峰

利用导数研究函数的单调性、极值和最值来证明不等式是函数、导数、不等式综合中的一个难点，也是近几年高考的热点．解决此类问题主要是把不等式的证明转化为利用导数研究函数的单调性或求最值，而关键是如何根据不等式的结构特征构造一个可导函数，再用导数证明不等式．现在归纳几种常见的构造函数的方法，具体如下．

一、常用模型构造函数

例1设函数f（x）在R上的导函数为f′（x），且2f（x）＋xf′（x）＞0，求证：f（x）＞0在R上恒成立．

解答由已知，令x＝0得f（x）＞0．

令g（x）＝x2f（x），则g′（x）＝x［2f（x）＋xf′（x）］，

① 当x＞0时，有所以函数g（x）单调递增，所以当x＞0时，g（x）＞g（0）＝0，从而f（x）＞0．

② 当x＜0时，有所以函数g（x）单调递减，所以当x＜0时，g（x）＞g（0）＝0，从而f（x）＞0．

综上，f（x）＞0在R上恒成立．

小结此题构造函数g（x）＝x2f（x），g′（x）＝x［2f（x）＋xf′（x）］，与条件2f（x）＋xf′（x）＞0密切相关，从条件特征入手，联想到常用求导公式模型，是我们构造函数的常用方法之一．现归纳两类常用模型：

1．关系式为“加”型

（1）若已知f′（x）＋f（x）≥0（≤0），构造［exf（x）］′＝ex［f′（x）＋f（x）］；

（2）若已知xf′（x）＋f（x）≥0（≤0），构造［xf（x）］′＝xf′（x）＋f（x）；

（3）若已知xf′（x）＋nf（x）≥0（≤0），构造［xnf（x）］′＝xnf′（x）＋nxn－1f（x）＝xn－1［xf′（x）＋nf（x）］．

2．关系式为“减”型

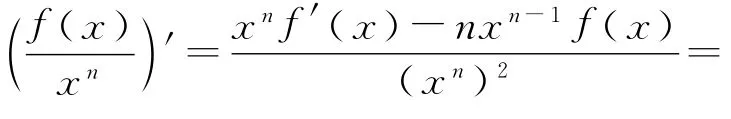
二、作差（商）构造函数

综上可知，当x＞－1时，有ln（x＋1）≤x．

小结证明f（x）≥g（x）对x∈D恒成立问题可以转化为f（x）－g（x）≥0对x∈D恒成立问题，等价于，即构造函数F（x）＝f（x）－g（x），证明F（x）min≥0；同样的，若g（x）＞0时，也可构造函数，证明G（x）min≥1．

三、用常见不等式构造函数

在学习过程中，同学们会发现不等式ex≥x＋1，x－1≥lnx在解题中会经常遇到，此组不等式可用作差构造函数证明，从图象中也很容易直观理解（如图1）．

图1

若令t＝x＋1，不等式的右侧变为lnt≤t－1；

四、形似构造函数

例3已知函数a＞1．证明：若a＜5，则对任意x1，x2∈ （0，＋ ∞），x1≠x2，有

小结此题经过等价变换后得到f（x1）＋x1＞f（x2）＋x2，两边有相似的结构，构造函数g（x）＝f（x）＋x，研究g（x）的性质作为突破口．对于本身具有对称性的双变量不等式证明问题，通过等价变形，利用相似结构构造函数是比较常见的．

五、换元法构造函数

例4已知函数g（x）＝logax（a＞0，且a≠1），其中a为常数．如果h（x）＝f（x）＋g（x）是增函数，且h′（x）存在零点（h′（x）为h（x）的导函数）．

（1）求a的值；

（2）设A（x1，y1），B（x2，y2）（x1＜x2）是函数y＝g（x）图象上的两点，g′（x0）＝为g（x）的导函数），证明：x1＜x0＜x2．

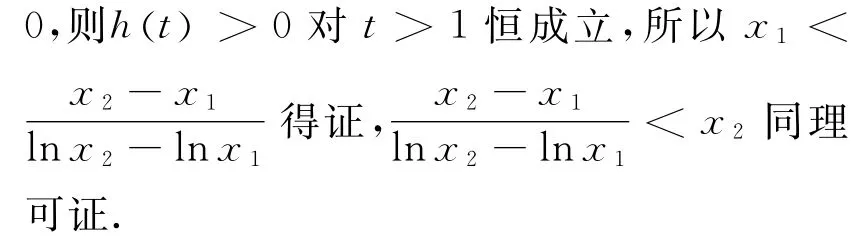
小结多元变量证明问题首先可以进行等价变形，根据变量特征进行换元达到减元的目的．此题中要证明变形后，剩下的变量x1，x2又是分式齐次的，容易想到令来换元．

六、主元法构造函数

令r（x）＝xlnx2－xlnx－x2＋x，那么r′（x）＝lnx2－lnx，在（0，x2］上，r′（x）＞0，所以r（x）在（0，x2］上单调递增．当x1＜x2时，r（x1）＜r（x2）＝0，即x1lnx2－x1lnx1－x2＋x1＜0，从而x0＞x1得到证明．对于同理可证，所以x1＜x0＜x2．

小结当变量比较多时，往往选择其中某个变量为主元，对其他变量“视而不见”，以达到减元目的．

在观察不等式结构特征、选择何种方法构造函数前，很多题目需要对不等式进行变形，同学们不仅要关注变形的一些技巧问题，还要特别注意在不等式变形过程中的等价性问题，比如去分母注意不等号是否需要变向；变换过程中自变量的范围有没有发生改变；换元后有没有注意到新元的范围等等．