模糊Z-Quantale范畴的反射子范畴

邬宏伟, 汪开云

(陕西师范大学 数学与信息科学学院, 西安 710119)

Quantale理论[1]为研究非交换的C*-代数提供了新的格式刻画, 并给量子力学提供了新的数学模型[2]. 文献[3]将集系统应用到Quantale理论中, 作为Quantale的一般化, 引入了Z-Quantale的概念, 并研究了Z-Quantale及其范畴的若干性质. 文献[4]证明了Quantale范畴是Z-Quantale范畴的反射子范畴. Zadeh[5]提出了模糊集的概念, 文献[6]通过模糊序研究Quantale理论, 引入了模糊Quantale的概念, 并证明了模糊Quantale范畴同构于Quantale代数范畴, 从范畴论的角度说明了Quantale代数可视为Quantale的模糊化结构. 作为Z-Quantale结构的模糊化, 文献[7]引入了模糊Z-Quantale的概念, 并证明了模糊Z-Quantale范畴是模糊序半群范畴的反射子范畴. 在上述工作的基础上, 本文证明模糊Quantale范畴是模糊Z-Quantale范畴的反射子范畴, 并讨论由反射子构造的模糊Galois伴随.

1 预备知识

有关范畴论的相关内容可参见文献[8].

定义1[9]设L是完备格, *是L上的二元运算, 且满足:

1) ∀a,b,c∈L, (a*b)*c=a*(b*c);

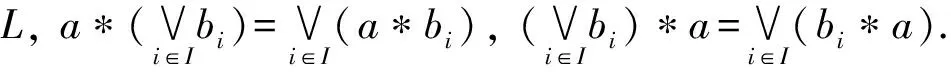
定义2[9]设L是Quantale, 若存在1∈L, 使得∀a∈L, 有a*1=1*a=a, 则称1是L的单位元, 此时称L是单位Quantale. 若∀a,b∈L, 有a*b=b*a, 则称L是交换Quantale.

若无特殊说明, 本文L均指交换的单位Quantale, 1是L的单位元.∀a∈L, 由Quantale的定义知,a&_是L上的保并映射, 所以其有右伴随, 记为a→-. ∀a,b,c∈L,a&b≤c当且仅当a≤b→c.

定义3[9]设L1和L2是Quantale,f:L1→L2是映射. 如果f保任意并和*运算, 则称f是从L1到L2的Quantale同态.

定义4[10-12]设X是集合,e:X×X→L是映射. 如果e满足:

1) ∀x∈X,e(x,x)≥1;

2) ∀x,y,z∈X,e(x,y)*e(y,z)≤e(x,z);

3) ∀x,y∈X,e(x,y)≥1,e(y,x)≥1蕴含x=y.

则称e是X上的一个模糊偏序, 称偶对(X,e)是一个模糊偏序集.

设(X,e)是模糊偏序集, 则≤e={(x,y)|e(x,y)≥1}是一个分明偏序. 若无特殊说明, 本文在模糊偏序集(X,e)框架下的偏序均指≤e, 简记为≤.

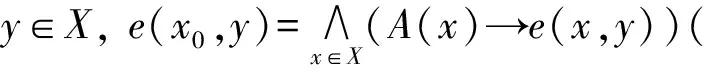
定义6[12,14]设(X,e)是模糊偏序集,A∈LX. 如果∀x,y∈X,e(x,y)*A(x)≤A(y)(或e(x,y)*A(y)≤A(x)), 则称A是模糊上集(或模糊下集).

注2设(X,e)是模糊偏序集, ∀A∈LX, 定义↓A,↑A∈LX为∀x∈X,

则↓A是模糊下集, ↑A是模糊上集.

定义9[11-12]设(X,eX),(Y,eY)是模糊偏序集,f:X→Y是映射.

1) 如果∀x,y∈X,eX(x,y)≤eY(f(x),f(y)), 则称f保模糊序;

定义10[6]若(X,e)是模糊偏序集, (X,·)是半群, 且∀a,b,c,d∈X,e(a,b)*e(c,d)≤e(a·c,b·d), 则称(X,·,e)是模糊序半群.

定义11[6]设(X1,·,e1)和(X2,·,e2)是模糊序半群,f:X1→X2是映射. 如果f保模糊序, 且∀a,b∈X1,f(a·b)=f(a)·f(b), 则称f是从X1到X2的模糊序半群同态.

定义12[6]设(X,e)是模糊完备格, (X,⊗)是半群. 若∀a∈X,D∈LX,

(1)

则称(X,⊗,e)是模糊Quantale, 简称X是模糊Quantale.

例2设(S,·,e)是模糊序半群, 用LD(S)表示S模糊下集的全体. 在LD(S)上定义二元运算⊗:

则(LD(S),⊗,sub)是模糊Quantale.

定义13[6]设X,Y是模糊Quantale,f:X→Y是映射. 如果f保模糊并和⊗运算, 则称f是从X到Y的模糊Quantale同态.

记L-OSG为以模糊序半群为对象, 以模糊序半群同态为态射的范畴; 记L-Quant为以模糊Quantale为对象, 以模糊Quantale同态为态射的范畴.

2 主要结果

定义14[7]L-OSG上的模糊集系统ZL是一个映射, 其中对任意的模糊序半群(S,·,e),ZL(S)是由(S,·,e)的模糊下集构成的子集族, 且满足下列条件：

1) ∀s∈S,ls∈ZL(S);

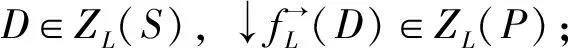
3) (ZL(S),⊗,sub)是(LD(S),⊗,sub)的模糊子序半群;

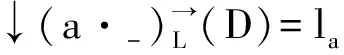
以下总假设在L-OSG上给定了一个模糊集系统ZL.

定义16[7]设(S,⊗,e)是模糊ZL-完备序半群. 若∀a∈S,D∈ZL(S), 式(1)成立, 则称(S,⊗,e)是模糊Z-Quantale, 简称S是模糊Z-Quantale.

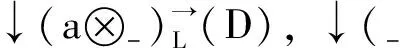
例31) 设(S,·,e)是模糊序半群,ZL(S)=LD(S), 则S是模糊Z-Quantale当且仅当S是模糊Quantale; 2) 设(S,·,e)是模糊序半群,ZL(S)={ls|s∈S}, 则S是模糊Z-Quantale.

记L-ZQuant为以模糊Z-Quantale为对象, 模糊Z-Quantale同态为态射的范畴. 易见,L-Quant是L-ZQuant的子范畴.

定义18[17]设(X,⊗,e)是模糊Quantale,j:X→X是保模糊序映射. 若j满足:

1) ∀x∈X,e(x,j(x))≥1;

2) ∀x,y∈X,e(x⊗j(y),j(x⊗y))≥1,e(j(x)⊗y,j(x⊗y))≥1.

则称j是X上的模糊预核映射.

命题1设(S,·,e)是模糊Z-Quantale. 定义映射j:LD(S)→LD(S)如下：

则j是LD(S)上的模糊预核映射.

证明: ∀U∈LD(S),x,y∈S, 有

于是j(U)∈LD(S), 所以j是良定的. 易见sub(U,j(U))≥1. ∀U,V∈LD(S), 有

于是j是保模糊序的. ∀U,W∈LD(S), 由(S,·,e)是模糊Z-Quantale, 得

同理可证sub(U⊗j(W),j(U⊗W))≥1, 所以j是LD(S)上的模糊预核映射.

引理1[17]设(X,⊗,e)是模糊Quantale,j是X上的模糊预核映射, 则(Xj,⊗j,e)是模糊Quantale, 其中Xj={A⊆X|j(A)=A}, 且∀x,y∈Xj,x⊗jy=j(x⊗y).

定理1L-Quant是L-ZQuant的反射子范畴.

证明: 设(S,·,e)是模糊Z-Quantale, 由引理1知, 命题1定义的模糊预核映射j的不动点之集LD(S)j是模糊Quantale. 定义映射ηS:S→LD(S)j如下: ∀s∈S,ηS(s)=ls. 则∀x∈S, 有

于是ηS(s)∈LD(S)j, 所以ηS是良定的. ∀x,y∈S, 有

ηS(x·y)=j(ηS(x·y))=j(ηS(x)⊗ηS(y))=ηS(x)⊗jηS(y).

∀U∈LD(S)j, 有j(U)=U. 所以∀s∈S, 有

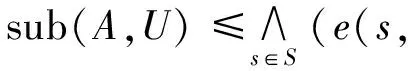
而

所以

∀V∈LD(S)j,f(V)=h(V).

∀B,C∈LLD(S)j, 有

f(B⊗jC)=h(j(B⊗C))=h(B⊗C)=h(B)☆h(C)=f(B)☆f(C).

∀B∈LLD(S)j, 有

从而k=f, 所以L-Quant是L-ZQuant的反射子范畴.

2) 当ZL(S)={ls|s∈S}时,L-ZQuant恰为L-OSG. 于是由定理1,L-Quant是L-OSG的反射子范畴[6].

3 反射子构造的模糊Galois伴随

定义19[18]设(X,eX),(Y,eY)是模糊偏序集,f:X→Y,g:Y→X是保模糊序映射. 如果∀x∈X,y∈Y,eY(f(x),y)=eX(x,g(y)), 则称(f,g)为X和Y之间的一个模糊Galois伴随, 此时,f称为g的左伴随,g称为f的右伴随.

定义21[14]设(X,⊗,e)是模糊Quantale,A⊆X, 则∩{S⊆X|S是X的模糊子Quantale, 且A⊆S}是模糊子Quantale, 称为由A生成的模糊子Quantale, 记作〈A〉.

设(S,·,e)是模糊Z-Quantale. 由定理1知L-Quant是L-ZQuant的反射子范畴, 则存在万有映射ηS及反射子F:L-ZQuant→L-Quant, 其中ηS:S→F(S)是模糊Z-Quantale同态. 若S是模糊Quantale, 则存在唯一的模糊Quantale同态εS:F(S)→S, 使得εS∘ηS=idS.

命题2设(S,·,e)是模糊Z-Quantale, 则F(S)是由ηS的像集ImηS生成的模糊Quantale.

证明: 设X=〈ImηS〉⊆F(S),φ:S→X是ηS:S→F(S)的余限制,i:X→F(S)是含入映射, 则i∘φ=ηS. 由于L-Quant是L-ZQuant的反射子范畴, 则存在唯一的模糊Quantale同态h:F(S)→X, 使得h∘ηS=φ. 从而ηS=i∘φ=i∘h∘ηS, 所以i∘h=idF(S). 因此i是满的, 于是X=F(S), 即F(S)是由ImηS生成的模糊Quantale.

命题3设(S,·,e)是模糊Z-Quantale. ∀b∈F(S), 定义映射kb:F(S)→L如下:

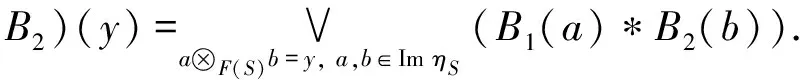
由于F(S)是模糊Quantale, 则∀z∈F(S), 有

其中I: A→F(S)是含入映射. 所以A是F(S)的模糊子Quantale. ∀y∈ImηS, 定义映射Xy: ImηS→L如下：

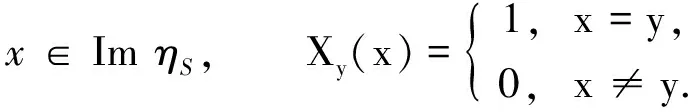
命题4设(S,·,e)是模糊Quantale, 则ηS∘εS≥idF(S).

因此ηS∘εS≥idF(S).

引理2[18-19]设(X,eX),(Y,eY)是模糊偏序集,f:X→Y,g:Y→X是保模糊序映射, 则(f,g)是模糊Galois伴随当且仅当f∘g≤idY,g∘f≥idX.

定理2设(S,·,e)是模糊Quantale, 则(εS,ηS)是模糊Galois伴随.

证明: 由命题4与引理2可得结论.