区间直觉模糊集相似度构造
邵丽鹏,潘小东
(西南交通大学数学学院, 四川 成都 611756)
1986年,保加利亚学者Atanassov教授给出了直觉模糊集的概念[1]。随后,Atanassov等推广了直觉模糊集,提出了区间直觉模糊集[2]。区间直觉模糊集相似度有着广泛的应用,是学者们关注的热点。徐泽水[3]基于海明距离、欧几里得距离和基于Hausdorff度量的海明距离、欧几里得距离,提出4个带有权重的区间直觉模糊集相似度。周珍[4]利用平均值和Hausdorff测度将Hong定义的Vague集相似度扩展到区间值Vague集,提出区间Vague集相似度。杨伟萍等[5]对文献[6]提出的直觉模糊集相似度进行改进,并将改进好的直觉模糊集相似度扩展到区间直觉模糊集。楚俊峰等[7]考虑了犹豫度对隶属度和非隶属度的影响,提出区间直觉模糊数(集)相似度。邱婷婷等[8]给出一种新的区间直觉模糊集相似度,该相似度考虑了对应隶属度之间的最大、最小值与非隶属度的最大、最小值。Meng等[9]首先基于直觉模糊熵,提出区间直觉模糊熵,进而基于熵和相似度的关系,提出区间直觉模糊集相似度。 Liu等[10]提出了区间直觉模糊有序加权余弦相似度,并应用在群体决策问题上。邓冠男等[11]利用模糊集贴近度构造区间值模糊集贴近度。刘鹏惠[12]利用模糊集贴近度构造直觉模糊集相似度。目前为止,区间直觉模糊集相似度的研究已经很多,但是没有一种专门或者系统的利用直觉模糊集相似度构造区间直觉模糊集相似度。虽有很多文献将直觉模糊集相似度推广到区间直觉模糊集,但是没有固定的一套系统如文献[3-4]。基于此,本文对区间直觉模糊集相似度的构造进行系统的研究,并应用到模式识别。
1 预备知识
1.1 直觉模糊集的相关知识
定义1[1]设X为一非空集合,X上的直觉模糊集A定义为
A={〈x,uA(x),vA(x)〉|x∈X}。
其中映射uA:X→[0,1],vA:X→[0,1]分别为直觉模糊集A的隶属函数和非隶属函数,uA(x),vA(x)分别为X中元素x属于直觉模糊集A的隶属度和非隶属度,且0≤uA(x)+vA(x)≤1,记πA(x)=1-uA(x)-vA(x),称πA(x)为犹豫度,很明显0≤πA(x)≤1。
X上的全体直觉模糊集一般记为IFSs(X)。
直觉模糊集A的补集记作AC,AC={〈x,vA(x),uA(x)〉x∈X}。
X上的直觉模糊集A和B有如下运算:
1)A⊆B⟺∀x∈X,uA(x)≤uB(x),vA(x)≥vB(x);
2)A=B⟺∀x∈X,uA(x)=uB(x),且vA(x)=vB(x)。
定义2[13]设A,B是有限论域X上2个直觉模糊集,S为一个映射:IFS×IFS→[0,1],如果S(A,B)满足以下性质:
(S1)0≤S(A,B)≤1;
(S2)S(A,B)=1当且仅当A=B;
(S3)S(A,B)=S(B,A);
(S4)如果A⊆B⊆C,则S(A,C)≤S(A,B),S(A,C)≤S(B,C)。
则称S(A,B)是直觉模糊集A与B之间的相似度。
设A∈IFSs(X),B∈IFSs(X),下面是文献中部分已知直觉模糊集相似度。
1)Boran等[13]提出的相似度。
2)文献[14]提出的相似度。
1.2 区间直觉模糊集的相关知识
定义3[2]设X是一个非空集合,则称
为区间直觉模糊集,其中





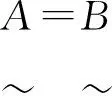

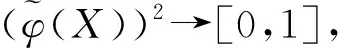
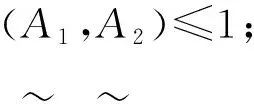
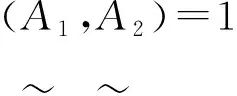

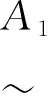

周珍[4]分别利用区间数的中点值、Hausdorff测度,得到的区间直觉模糊集相似度为:
2 区间直觉模糊集相似度的构造
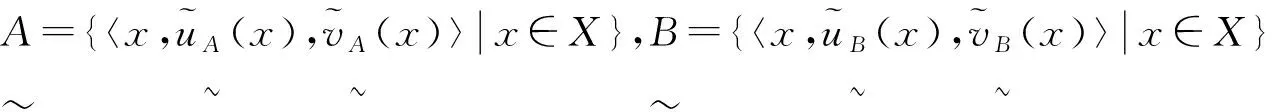
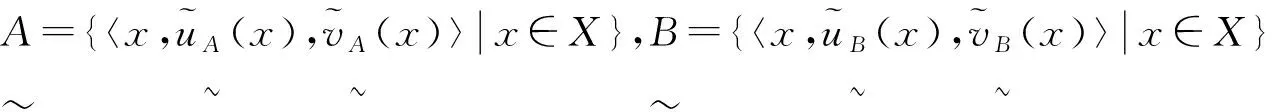
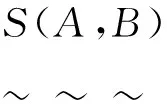
证明1)S是IFSs(X)上的直觉模糊集的相似度。

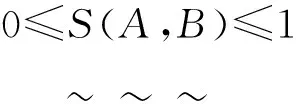
2)必要性。
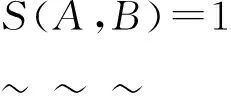
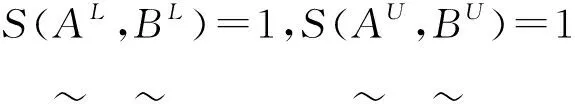
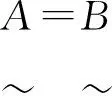
充分性。
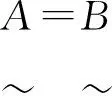


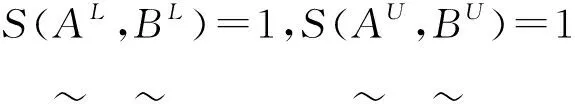
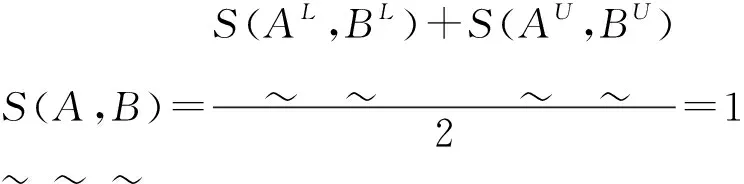

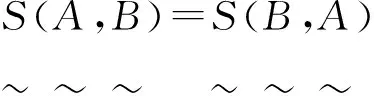

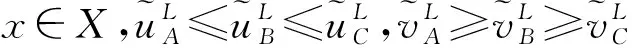
于是,由直觉模糊集的包含的定义知:
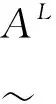
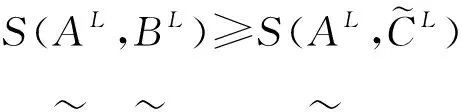

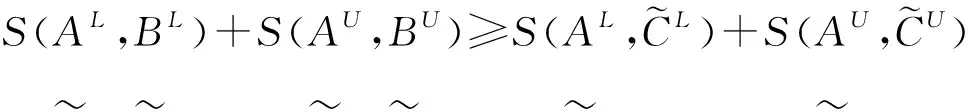
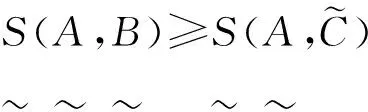
由文中提出的定理及文献[13]、[14]给出的直觉模糊集相似度公式,给出区间直觉模糊集相似度公式:
1)由文献[13]得
2)由文献[14]得
3 区间直觉模糊相似度在模式识别中的应用分析
模糊模式识别是模式识别的一种,其研究对象具有模糊性,研究内容是在论域U中有已知模型A1,A2,…,An,未知模式B,根据择近原则确定B与Ai(i=1,2,…,n)中哪一个更接近。其步骤如下:
1)利用区间直觉模糊相似度公式分别计算S(B,A1),S(B,A2),…,S(B,An);
2)利用择近原则,取J={i|maxS(B,Ai),i=1,2,…,n},则B属于模式Ai。
例引用文献[7]的例子,其数据如表1所示,根据本文提出的2个区间直觉模糊相似度公式及周珍[4]提出的2个区间直觉模糊相似度S1、S2和楚俊峰[7]提出的区间直觉模糊相似度SAB且假设各个元素的权重相同,得到表2。

表1 区间直觉模糊集

表1(续)
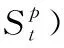
表2 相似度的比较(其中p=1,t=2对于
注:表2中S1、S2、SAB的相似度的数据来自文献[7]。
通过分析比较上述5种相似度公式,可以看出本文提出的2个区间直觉模糊集相似度公式有较好的识别效果。
4 结论
本文主要讨论将区间直觉模糊集拆分成2个直觉模糊集,进而利用已知直觉模糊集相似度公式,提出区间直觉模糊集相似度,为区间直觉模糊集相似度的构造提供了新的方法。在未来的研究中,将讨论该相似度的性质及更多的应用。

