E-不变凸模糊集

刘卫锋, 许宏伟

(郑州航空工业管理学院 数理系, 郑州 450015)



E-不变凸模糊集

刘卫锋*, 许宏伟

(郑州航空工业管理学院 数理系, 郑州 450015)

通过将不变凸集、E-凸集和凸模糊集相结合,提出了一种新的广义凸模糊集—E-不变凸模糊集,使得不变凸模糊集和凸模糊集成为它的特例,并初步研究了E-不变凸模糊集的性质.

凸模糊集;E-不变凸模糊集; 不变凸模糊集; 模糊集

由于凸集在凸分析、函数论、最优化理论及其他数学分支中均有广泛的应用[1-5],因此,对凸集及其性质进行研究和推广一直是数学应用和基础研究领域的一个重要课题.在凸集概念基础上,文献[1-3]引进了p-凸集和绝对p-凸集,并探讨它们的性质;文献[6]对p-凸集和绝对p-凸集的性质进行了系统的研究;文献[7]提出了p-完美凸集和绝对p-完美凸集;文献[8]引入了E-凸集和E-凸函数等概念,推广了凸集;文献[9-10]指出文献[8]中存在的错误,完善了E-凸集和E-凸函数;文献[11]提出了不变凸集理论,推广了凸集理论;文献[12]将不变凸集与E-凸集相结合,提出了E-不变凸集.与凸集理论一样,凸模糊集在模糊最优化研究中也具有非常重要的作用,文献[13]对凸模糊集作了较为系统的研究;文献[14]讨论了凸模糊集的性质;文献[15]引入T-p-凸模糊集,并讨论了其性质;文献[16]给出了基于t-范上的凸模糊集,推广了凸模糊集;文献[17-18]分别提出了一种(λ,μ]凸模糊集和(∈,∈q(λ,μ))凸模糊集;文献[19]提出不变凸模糊集的概念,并对其性质作了初步研究.

在上述研究基础上,本文尝试将不变凸集、E-凸集与凸模糊集相结合,得到一种更加一般化的广义凸模糊集—E-不变凸模糊集,使得凸模糊集、文献[19]中的不变凸模糊集成为它的特例,并对E-不变凸模糊集的性质进行了初步研究.本文研究进一步拓展了凸模糊集的概念,丰富了凸模糊集理论.

1 相关概念

定义1[4]设集合A⊂Rn,称A为凸集,若有

λx+(1-λ)y∈A,∀x,y∈A,∀λ∈[0,1].

定义2[8]设集合A⊂Rn,称A为E-凸集,若存在映射E:Rn→Rn,有

λE(x)+(1-λ)E(y)∈A,∀x,y∈A,∀λ∈[0,1].

定义3[11]设集合A⊂Rn,称A为不变凸集,若存在映射η:Rn×Rn→Rn,有

y+αη(x,y)∈A,∀x,y∈A,∀α∈[0,1].

定义4[12]设集合A⊂Rn,称A为E-不变凸集,若存在映射η:Rn×Rn→Rn和E:Rn→Rn,有

E(y)+αη(E(x),E(y))∈A,∀x,y∈A,∀α∈[0,1].

定义5[13]设论域为Rn,称A为论域Rn上的模糊集,若存在映射

A:Rn→[0,1],x→A(x).

论域Rn上的全体模糊集记作F(Rn).

定义6[19]设A∈F(Rn),称A为不变凸模糊集,若存在映射η:Rn×Rn→Rn,有

A(y+αη(x,y))≥A(x)∧A(y),∀x,y∈Rn,∀α∈[0,1].

条件C[19]设映射η:Rn×Rn→Rn,称η满足条件C,如果有

η(y,y+tη(x,y))=-tη(x,y),

η(x,y+tη(x,y))=(1-t)η(x,y),

∀x,y∈Rn,∀t∈[0,1].

2 主要结果

定义7 设A∈F(Rn),称A为E-不变凸模糊集,若存在映射η:Rn×Rn→Rn和E:Rn→Rn,有

A(E(y)+αη(E(x),E(y)))≥

A(E(x))∧A(E(y)),∀x,y∈Rn,∀α∈[0,1].

显然,当E为恒等映射时,E-不变凸模糊集就是不变凸模糊集.因此,E-不变凸模糊集是不变凸模糊集和凸模糊集的推广.

定理1 任意凸模糊集是E-不变凸模糊集,任意不变凸模糊集是E-不变凸模糊集.

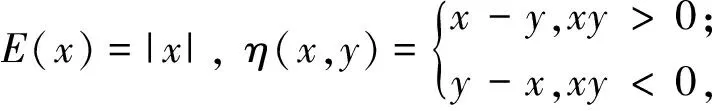
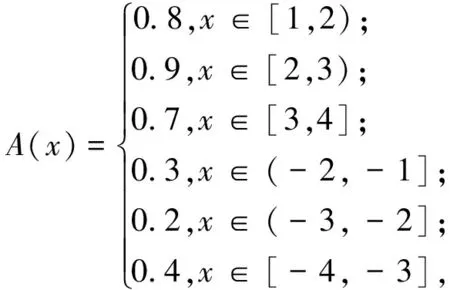
则A是关于η的E-不变凸模糊集,而A不是凸模糊集,也不是不变凸模糊集.

首先,可以验证,A是关于η的E-不变凸模糊集.

下面给出8种情况下的验证,其余情况的验证均可归结为下面这8种情况.

(1) 当x,y∈[1,2)时,显然xy>0,且E(x)=x,E(y)=y,从而A(E(x))=A(x)=0.8,A(E(y))=A(y)=0.8,η(E(x),E(y))=η(x,y)=x-y,于是

A(E(y)+αη(E(x),E(y)))=

A(y+α(x-y))=A(αx+(1-α)y)=

0.8≥A(E(x))∧A(E(y)).

(2) 当x,y∈(-2,-1]时,显然xy>0,且E(x)=-x,E(y)=-y,从而A(E(x))=A(-x)=0.8,A(E(y))=A(-y)=0.8,η(E(x),E(y))=η(-x,-y)=-x+y,于是

A(E(y)+αη(E(x),E(y)))=

A(-y+α(-x+y))=

A(α(-x)+(1-α)(-y))=

0.8≥A(E(x))∧A(E(y)).

(3) 当x∈[1,2),y∈[2,3)时,显然xy>0,且E(x)=x,E(y)=y,A(E(x))=A(x)=0.8,A(E(y))=A(y)=0.9,η(E(x),E(y))=η(x,y)=x-y,于是

A(E(y)+αη(E(x),E(y)))=

A(y+α(x-y))=A(αx+(1-α)y)=

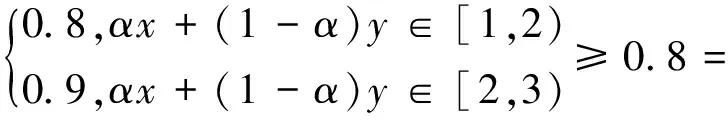
A(E(x))∧A(E(y)).

(4) 当x∈[1,2),y∈[3,4]时,显然xy>0,且E(x)=x,E(y)=y,从而A(E(x))=0.8,A(E(y))=0.7,η(E(x),E(y))=x-y,于是

A(E(y)+αη(E(x),E(y)))=

A(y+α(x-y))=A(αx+(1-α)y)=

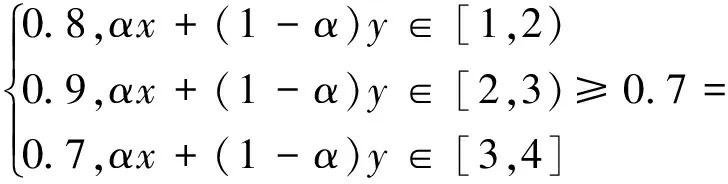
A(E(x))∧A(E(y)).

(5) 当x∈(-2,-1],y∈[-3,-2)时,有xy>0,且E(x)=-x,E(y)=-y,从而A(E(x))=0.8,A(E(y))=0.9,η(E(x),E(y))=-x+y,于是

A(E(y)+αη(E(x),E(y)))=

A(-y+α(-x+y))=

A(α(-x)+(1-α)(-y))=

0.8=A(E(x))∧A(E(y)).

(6) 当x∈(-2,-1],y∈[-4,-3]时,显然xy>0,且E(x)=-x,E(y)=-y,从而A(E(x))=0.8,A(E(y))=0.7,η(E(x),E(y))=-x+y,于是

A(E(y)+αη(E(x),E(y)))=

A(-y+α(-x+y))=

A(α(-x)+(1-α)(-y))=

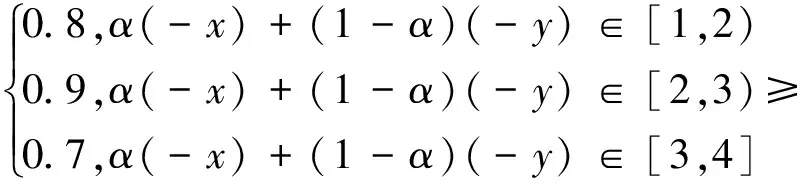
0.7=A(E(x))∧A(E(y)).

(7)当x∈[3,4],y∈[-4,-3]时,显然有xy<0,且E(x)=x,E(y)=-y,从而A(E(x))=A(E(y))=0.7,η(E(x),E(y))=η(x,-y)=x+y,于是

A(E(y)+αη(E(x),E(y)))=

A(-y+α(x+y))=

A(αx+(1-α)(-y))=0.7≥

A(E(x))∧A(E(y)).

(8) 当x∈[1,2),y∈[-4,-3]时,显然xy<0,且E(x)=x,E(y)=-y,从而A(E(x))=0.8,A(E(y))=0.7,η(E(x),E(y))=x+y,于是

A(E(y)+αη(E(x),E(y)))=

A(-y+α(x+y))=

A(αx+(1-α)(-y))=

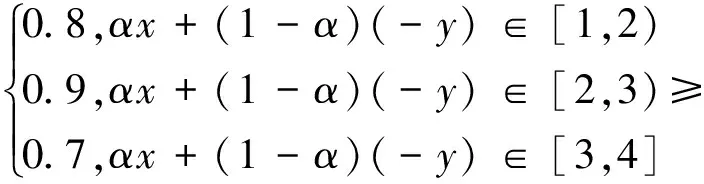
0.7=A(E(x))∧A(E(y)).

A(α0x0+(1-α0)y0)=A(-2)=

0.2<0.3=0.8∧0.3=A(x0)∧A(y0).

故A不是凸模糊集.

再次,A不是不变凸模糊集.事实上,令x0=1,y0=-1,α0=0.5,则有

A(y0+α0η(x0,y0))=A(-2)=

0.2<0.4=0.7∧0.4=A(x0)∧A(y0).

故A不是不变凸模糊集.

例1说明E-不变凸模糊集是凸模糊集和不变凸模糊集的真推广.

定义8 设A∈F(Rn),称A为E-不变强凸模糊集,若存在映射η:Rn×Rn→Rn和E:Rn→Rn,有

A(E(y)+αη(E(x),E(y)))>A(E(x))∧A(E(y)),∀x,y∈Rn,x≠y,∀α∈(0,1).

定义9 设A∈F(Rn),称A为E-严格不变凸模糊集,若存在映射η:Rn×Rn→Rn和E:Rn→Rn,有

A(E(y)+αη(E(x),E(y)))>A(E(x))∧A(E(y)),∀x,y∈Rn,当x≠y时,A(E(x))≠A(E(y)),∀α∈(0,1).

定理2 设A,B∈F(Rn)是E-不变凸模糊集,则A∩B是E-不变凸模糊集.

证明 ∀x,y∈Rn,由于集合A,B均为E-不变凸模糊集,因此存在映射η:Rn×Rn→Rn和E:Rn→Rn,对于∀α∈[0,1],有

A(E(y)+αη(E(x),E(y)))≥

A(E(x))∧A(E(y)),

B(E(y)+αη(E(x),E(y)))≥

B(E(x))∧B(E(y)).

于是

A(E(y)+αη(E(x),E(y)))∧

所以, A∩B是E-不变凸模糊集.

可以将定理2推广至任意多个集合的情况.

现将文献[19]中的条件C进行推广,并将推广条件记为条件C*:

条件C*设映射η:Rn×Rn→Rn,E:Rn→Rn,称η满足条件C*,如果有

η(E(y),E(y)+tη(E(x),E(y)))=

-tη(E(x),E(y)),

η(E(x),E(y)+tη(E(x),E(y)))=

(1-t)η(E(x),E(y)),

∀x,y∈Rn,∀t∈[0,1].显然,当E为恒等映射时,条件C*就是条件C.当E为恒等映射,且η(x,y)=x-y,条件C*自然成立.

定理4 设A∈F(Rn),存在映射η:Rn×Rn→Rn和E:Rn→Rn,且η满足条件C*,若存在α∈(0,1),使

A(E(y)+αη(E(x),E(y)))≥

A(E(x))∧A(E(y)),∀x,y∈Rn,

则

B={α∈(0,1)|A(E(y)+αη(E(x),E(y)))≥

A(E(x))∧A(E(y)),∀x,y∈Rn}

在(0,1)上是稠密的.

证明 (反证法) 设B在(0,1)上不是稠密的,则∃α0∈(0,1)及邻域N(α0),使得N(α0)∩B=Φ.

令α1=inf{α∈B|α≥α0},α2=sup{α∈B|α≤α0},则有0≤α2<α1≤1.

由于max{α,1-α}∈(0,1),取β1,β2∈B,使

β1≥α1,β2≤α2,且max{α,1-α}(β1-β2)<α1-α2.

设α′=αβ1+(1-α)β2=β2+α(β1-β2).现证明α′∈B,即证

A(E(y)+α′η(E(x),E(y)))>

A(E(x))∧A(E(y)).

利用条件C*,可得

E(y)+α′η(E(x),E(y))=

E(y)+β2η(E(x),E(y))+

α(β1-β2)η(E(x),E(y))=

E(y)+β2η(E(x),E(y))+

E(y)+β2η(E(x),E(y))+

β1η(E(x),E(y))+

E(y)+β2η(E(x),E(y))+

β1η(E(x),E(y))+

E(y)+β2η(E(x),E(y))+αη(E(y)+

β1η(E(x),E(y)),E(y)+β2η(E(x),E(y)))),

因此,有

A[E(y)+α′η(E(x),E(y))]=

A[E(y)+β2η(E(x),E(y))+

αη(E(y)+β1η(E(x),E(y)),E(y)+

β2η(E(x),E(y))))]≥

A(E(y)+β1η(E(x),E(y)))∧

A(E(y)+β2η(E(x),E(y)))≥

(A(E(x))∧A(E(y)))∧

(A(E(x))∧A(E(y)))=

A(E(x))∧A(E(y)),

所以,α′∈B.

若α′≥α0,则0≤β2≤α2<α1≤α′≤1,从而α′-β2≥α1-α2,又

α′-β2=αβ1+(1-α)β2-β2=

α(β1-β2)<α1-α2,

于是产生矛盾.

若α′<α0,则0≤α′≤α2<α1≤β1≤1,从而β1-α′≥α1-α2,又

β1-α′=β1-(αβ1+(1-α)β2)=

(1-α)(β1-β2)<α1-α2，

同样产生矛盾.

故B在(0,1)上是稠密的.

定义10 设A∈F(Rn),称A为E-不变下半连续的,若存在映射η:Rn×Rn→Rn和E:Rn→Rn,有

A(E(x))-ε≤A(E(y)),∀x,y∈Rn,∀ε>0,∃δ>0,且‖E(y)-E(x)‖<δ.

定理5 设A∈F(Rn)是E-不变下半连续的,且η满足条件C*,若∃α∈(0,1),有

A(E(y)+αη(E(x),E(y)))≥

A(E(x))∧A(E(y)),∀x,y∈Rn，

则A是E-不变凸模糊集.

证明 (反证法) 设A不是E-不变凸模糊集,则∃x,y∈Rn,α′∈(0,1),使

A(E(y)+α′η(E(x),E(y))<

A(E(x))∧A(E(y)).

设B={α∈(0,1)|A(E(y)+αη(E(x),E(y)))≥A(E(x))∧A(E(y)),∀x,y∈Rn},则由定理4可知,∃αn∈B,有αn→α′(n→∞).

定义

E(yn)=E(y)+α′η(E(x),E(y))-

E(y)+α′η(E(x),E(y))-

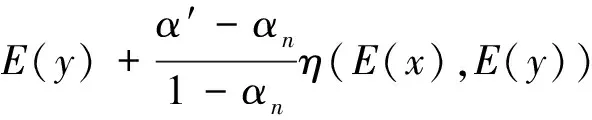
则E(yn)→E(y)(n→∞).现证明E(y)+α′η(E(x),E(y))=E(yn)+αnη(E(x),E(yn)).

E(yn)+αnη(E(x),E(yn))=

E(y)+αnη(E(x),E(y))+

E(y)+α′η(E(x),E(y)),

由于A是E-不变下半连续的,且E(yn)→E(y)(n→∞),故

A(E(yn))>A(E(y))-ε,∀n>N,其中N>0.

于是

A(E(y)+α′η(E(x),E(y)))=

A(E(yn)+αnη(E(x),E(yn)))≥

A(E(x))∧A(E(yn))≥

A(E(x))∧A(E(y)-ε)≥

A(E(x))∧A(E(y)).

由ε的任意性可知,A(E(y)+α′η(E(x),E(y)))≥A(E(x))∧A(E(y)),这与通过假设得到的不等式A(E(y)+α′η(E(x),E(y))

所以,A是E-不变凸模糊集.

定理6 设A∈F(Rn)是E-不变下半连续的,且η满足条件C*,若∃α∈(0,1),有

A(E(y)+αη(E(x),E(y)))>

A(E(x))∧A(E(y)),∀x,y∈Rn,x≠y,

则A是E-不变强凸模糊集.

证明 与定理5类似,故省略.

定理7 设A∈F(Rn)是E-不变下半连续的,且η满足条件C*,若∃α∈(0,1),有

A(E(y)+αη(E(x),E(y)))>A(E(x))∧A(E(y)),∀x,y∈Rn,A(E(x))≠A(E(y)),

则A是E-严格不变凸模糊集.

证明 与定理5类似,故省略.

[2] SMON S. The sequence spacesl(pv) andm(pv)[J]. Proceedings of the London Mathematical Society,1965, 15(3): 422-436.

[3] 定光桂. 拓扑线性空间选讲[M].南宁:广西教育出版社,1987.

[4] 袁亚湘, 孙文瑜. 最优化理论与方法[M].北京:科学出版社,1997.

[5] 胡适耕. 泛函分析[M].北京:科学出版社, 2001.

[6] 刘 文, 王晶昕.p-凸集和绝对p-凸集的一些性质[J].辽宁师范大学学报(自然科学版), 1995, 18(1):5-9.

[7] 张 端, 刘旭飞, 冷岗松.p-完美凸集和绝对p-完美凸集[J].上海大学学报(自然科学版), 2010, 16(3):262-267.

[8] YOUNESS E A.E-convex sets,E-convex functions, andE-convex programming[J].Journal of Optimization Theory and Applications, 1999, 102(2):439-450.

[9] YANG X M. OnE-convex set,E-convex functions, andE-convex programming[J].Journal of Optimization Theory and Applications, 2001, 109(3):699-704.

[10] JIAN J B. Incorrect result forE-convex functions, andE-convex programming[J]. Mathematical Research and Exposition, 2003, 23(3):461-466.

[11] HANSON M A, MOND B. Convex transformable programming problems and convexity[J]. Journal of Information and Optimization Science, 1987, 8: 201-207.

[12] FULGA C, PREDA V. Nonlinear programming withE-preinvex and localE-preinvex functions[J]. European Journal of Operational Reseach, 2009, 192:737-743.

[13] ZADEH L A. Fuzzy sets[J].Inform and Control, 1965, 8:338-353.

[14] LIU Y M. Some properties of convex fuzzy sets[J].Journal of Mathematical analysis and applications, 1965, 111(1): 119-129.

[15] 洪平洲, 许景飞.T-p-凸Fuzzy集[J].赣南师范学院学报(自然科学版),1999(6):1-7.

[16] 鞠红梅,袁学海,陈图云.凸模糊子集的再定义[J].模糊系统与数学, 2001, 15(1):68-70.

[17] 顾 惠, 廖祖华. 广义Fuzzy凸集[J].模糊系统与数学, 2004, 18:153-156.

[18] GU H, LIAO Z H. (∈,∈q(λ,μ))-convex fuzzy set[J].模糊系统与数学, 2007, 21(1):92-96.

[19] 张 萍, 黄 虎, 王 早. 预不变凸模糊集的一些性质[J].纯粹数学与应用数学, 2006, 22(3):355-359.

E-Invex fuzzy set

LIU Weifeng, XU Hongwei

(Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015)

By combining invex set and E-convex set with convex fuzzy set， a new generalized convex fuzzy set defined as E-invex fuzzy set is proposed， so that convex fuzzy set and invex fuzzy set were made particular cases. Some properties of E-invex fuzzy set are investigated primarily in this paper．

convex fuzzy set; E-invex fuzzy set; invex fuzzy set; E-convex fuzzy set

2015-06-24.

河南省教育厅科学技术研究重点项目(12B110027)；郑州航空工业管理学院青年科研基金项目(2014113001).

1000-1190(2016)01-0005-05

O174

A

*E-mail: lwf0519@163.com.