基于安全约束的停机位分配问题的研究
陈 前, 乐美龙
(上海海事大学 科学研究院, 上海 201306)
基于安全约束的停机位分配问题的研究
陈 前*, 乐美龙
(上海海事大学 科学研究院, 上海 201306)
停机位在机场运作系统中扮演着重要的角色,如果没有制定高效合理的停机位分配方案,航班便不能按原计划准时到达预定的停机位.随着航班数量的不断增加,机场运作效率的提高面临重大挑战,因此需要对航班进行停机位的合理分配.同时,合理地控制各个停机位的空闲时间可以避免相邻机位航班的运行冲突.考虑到机场系统的安全运行约束,建立避免冲突的停机位分配模型,引入实例,采用遗传算法进行求解,得出停机位分配的甘特图,验证了模型的合理性与有效性,更加贴近实际,提高了机场运行效率.
航空运输管理; 机位分配; 效率; 安全运行; 遗传算法
合理的机位分配方案可以帮助航空公司减少由于机位分配而造成的时间延误,保持其所制定的固定航班时刻,也可以减少旅客从机位到机位以及机位到出、入口的步行时间和距离,提高旅客满意度.虽然民航得到了迅速的发展,但基础设施明显不足,限制了机场运营规模的扩大,因此停机位的优化分配问题就成为了一个很重要的问题.
关于机位分配问题,国内外研究方法注意可以归纳为3类:数学规划方法、人工智能方法、计算机仿真方法,乐美龙[1]等针对机场和航班非正常运行时机场停机位分配问题,建立了非正常运行条件下的机场停机位实时分配混合整数规划模型,模型考虑了实际操作中的飞机空中等待时间以及航班延误和停机位故障等突发状况,最后运用CPLEX软件求解;王志清[2]等考虑到在登机口实际运作调度中存在机场的时间限制,航班对的限制和机型与登机口的匹配等限制,提出了以图论为基础的旅客登机口优化模型,来实现缩短旅客步行距离和提高设施利用率.朱金福[3]等以尽量减少旅客行走距离,实现航班的快速衔接从而缩短旅客中转时间,减少航班延误为目标,设计了一种排序模拟退火算法以求解枢纽机场的停机位指派问题.杨文东[4]等分析了机场停机位指派的基本约束和附加约束,以航班延误和停机位空闲时间总和最小为目标函数,构建机场停机位指派模型,提出停机位航班连接树的概念和构造方法,设计指派模型的贪婪算法.Ching-Hui Tang[6]等考虑航班延迟而重新分配问题,将其分为预处理和实处理两个阶段,以最小化时间和空间一致性为目标建立模型.
停机位作为重要的机场资源,要保证旅客能够方便的上下飞机,转机以及进出港,合理的停机位分配可以大大提高机场服务水平.从文献中可以看出,为了提高操作性能,研究者们已经提出了精确的和启发式的方法来探索很多完美的和接近完美的解决方案.确切说来,精确的算法特别适合用来解决小规模问题.然而,实际上,很多大城市机场每天通常有至少几十个登机口用来调度.这种情况下,由于问题规模太大,传统的精确算法无法解决实际的问题.因此,很多研究普遍采用启发式方法来解决停机位分配的问题(遗传算法,禁忌搜索算法,模拟退火法,蚁群算法和他们的混合算法).在此运用遗传算法来解决问题,同时分析在原始停机位分配问题中添加一些安全性约束之后产生的一些影响.一般来说,遗传算法更适用于全局搜索.现阶段优化的目标基本多是以基于旅客行走距离最少、要最小化延误等待时间、使机场资源利用最大化等为目标,但是这些都很难反映机位分配过程的实质,也无法解决有限资源有效利用和航班延误等问题.
1 模型建立
地面运行冲突主要指的是在相邻机位的航班的进离港时间相近,但是都使用的是同样的滑行道时,就容易在滑行道上相遇造成堵塞,对后续航班都会造成影响,导致不能准时的停靠,所以每个航班在地面运行时都需要和其他航班活动保持一定的安全间隔时间;对于同一个机位同一时间段内不允许同一个机位被两架航班或以上来占用.飞机在机场地面运行过程中为了避免冲突,必须设置一个安全的距离间隔和安全时间间隔.无论是相邻机位之间需要安全缓冲时间还是同一机位上需要设定安全缓冲时间,这两个时间不相互影响,都是为了避免地面活动作业发生冲突,在此对于这两个时间做了一个简单的设定,将这两个安全缓冲时间都设定为相同的时间用表示来研究避免地面活动作业冲突的停机位分配问题.本文以合理使用停机位空闲时间作为优化目标,合理的安排空闲时间来避免地面活动带来的冲突而导致航班延误.
1.1 模型的假设条件
1) 对任意航班,都遵循先到先服务原则.
2) 依靠在相邻停机位的飞机相互独立,只有一条跑道.
3) 时间假设,因为机场运作是一个连续不断的过程,在此为了寻找一个全局最优解,截取其中一段时间来分析.
4) 假设停靠该机场的航班量和时间分布保持在机场容量许可的范围内,停机位分配来说,总是可以为任一个到达航班分配到一个停机位.
5) 假设在每个工作日开始以前,当日停机位分配所必须的基本信息是已知的.
1.2 模型的参数设定
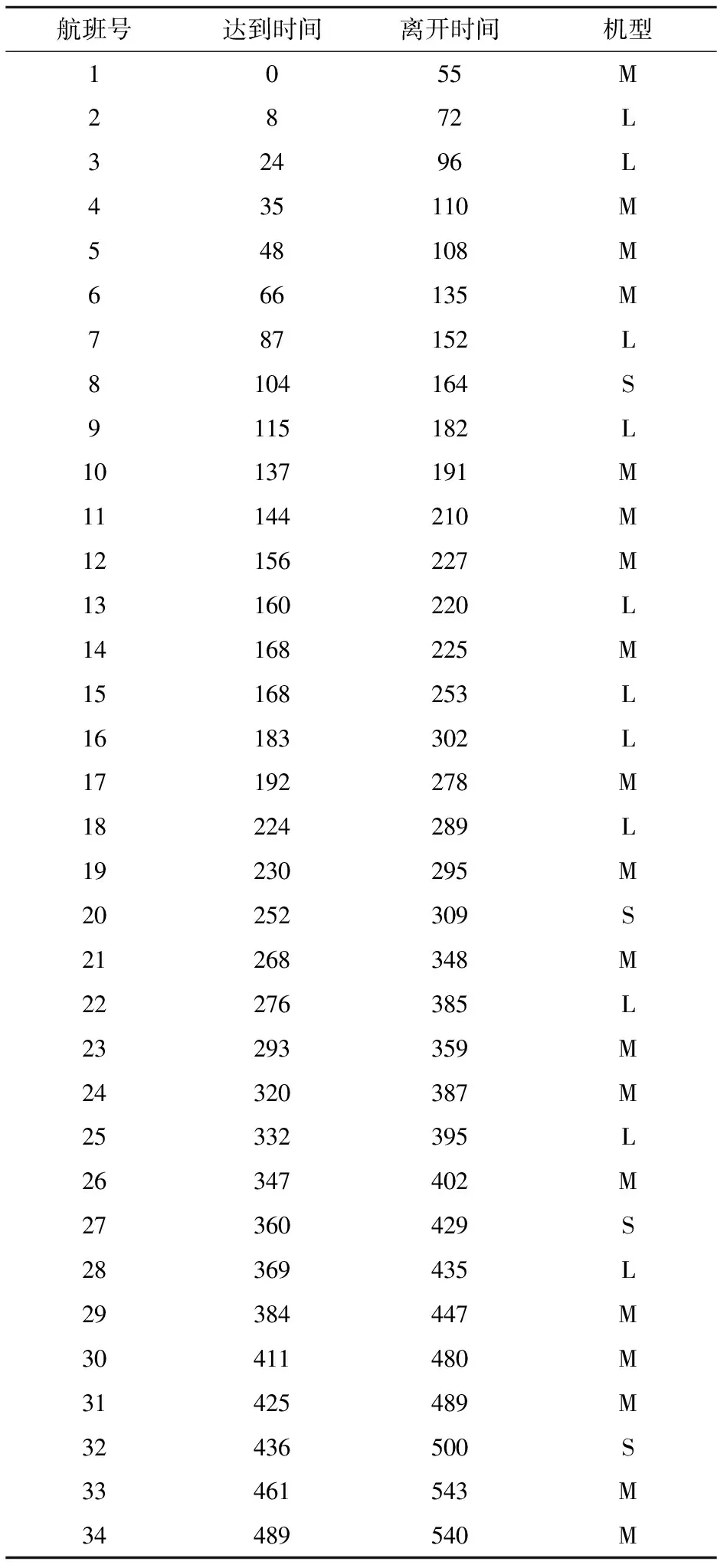
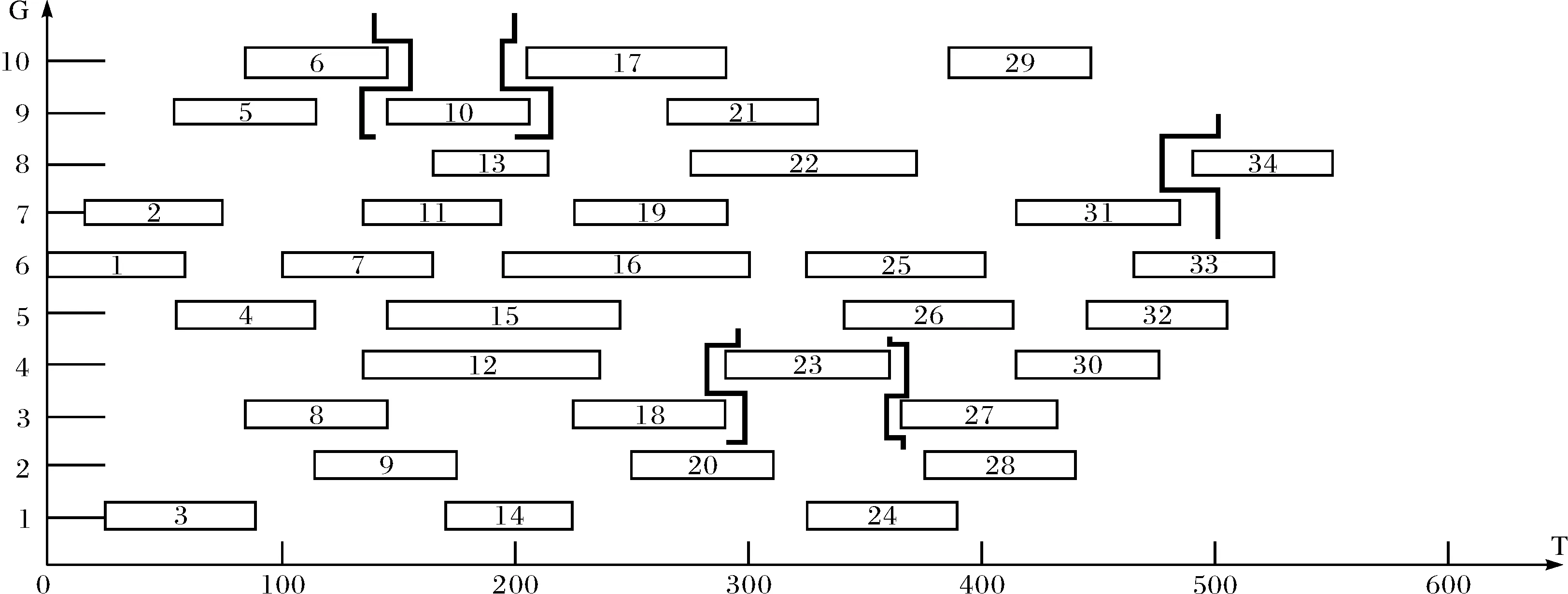
F表示航班集合;i,j表示航班下标;M表示机型集合,主要分为小、中、大3种机型,对应取值设为1、2、3,即Mk∈{1,2,3};k,l表示停机位下标;G表示停机位集合,停机位根据机型也分为小、中、大3种类型的停机位,对应取值设为1、2、3,即Gi∈{1,2,3};Ai表示航班i到达时间;Di表示航班i离港时间;Bk表示机位k的开放时间;Tq表示每个航班最小过站时间,设为40 min;Tp表示同一停机位最小安全缓冲时间,设为5 min;Si,j,k表示连续分配到同一停机位k的航班i和j之间的空闲时间;Pi,j表示航班i到航班j的旅客人数;wk,i表示停机位k到停机位l的距离;xi,k表示航班i分配到停机位k,xi,k=1 当且仅当分配飞机停到停机位k时,否则为0;yi,j,k,l表示分配至不同停机位的两架飞机之间的位置关系,当且仅当航班i分配至机位k,航班j分配至机位l时,yi,j,k,l=1;此时有yi,j,k,l=xi,kxj,l,可以将非线性转化为关于yi,j,k,l的线性表达式;表示相邻航班i和航班j被分配至同一个停机位k时,同时i 1.3 模型的目标函数 模型的目标函数公式为: (1) 1.4 模型的约束条件 模型的约束条件为: (2) Gk-Mi*xi,k≥0,∀i∈F,∀k∈G, (3) xi,k+xj,l≤,∀i,j∈F,∀k,∈G;i≠j, (4) (5) xi,k+xj,l-2yi,j,k,l≥0, ∀i,j∈F,∀k,l∈G;i≠j, (6) 如果(Dj-Ai)(Di-Aj)>0,则 (7) xi,k+xj,k-2yi,j,k≥0,∀i,j∈F,∀k,l∈G, (8) Si,j,k≥Tp,∀i,j∈F,∀k∈G, (9) xj,k-yo,j,k≥0,∀j∈F,∀k∈G, (10) Aj-Di≥Tpyi,j,k∀i,j∈F,∀k∈G, (11) Si,j,k≤Ai-Diyi,j,k,∀i,j∈F,∀k∈G, (12) Si,j,k≥Ajyi,j,k-Diyi,j,k∀i,j∈F,∀k∈G, (13) (14) xi,k,yi,j,k,yi,j,k,yo,j,k∈{0,1}, ∀i,j∈F,∀k∈G, (15) |Gi-Dj|≥Tpxi,kxj,k+1,∀i,j∈F,∀k∈G, |Gi-Dj|≥Tpxi,kxj,k+1,∀i,j∈F,∀k∈G, |Gj-Di|≥Tpxi,kxj,k+1,∀i,j∈F,∀k∈G, |Ai-Aj|≥Tpxi,kxj,k+1,∀i,j∈F,∀k∈G. (16) 约束条件2表示唯一性约束,一个航班只能分配到一个停机位;约束条件3表示机型与停机位的配对关系;约束条件4表示一个停机位在同一时刻只能分配给一个航班;条件5,6表示对yi,j,k,l取值;约束条件7,8表示对yi,j,k的取值;约束条件9表示的是分配到同一停机位的两个航班之间的空闲时间要大于等于安全缓冲时间;约束条件10表示的对第一个分配到k机位的变量yo,j,k的定义;约束条件15表示变量的取值范围;约束条件11表示的是对于分配到同一机位的两个连续航班之间最小间隔时间的定义;约束条件12和13表示的对同一机位两连续航班之间的空闲时间;约束条件14表示的对每个机位最后一个航班的离开时间的定义;约束条件15表示的是各个变量的取值范围.约束条件16是为了避免分配到相邻停机位的两个航班进出产生冲突的最小时间,以此来保证相邻机位之间不会出现运行冲突. 1.5 解决方法 遗传算法包括全部的染色体或者每一代的个体染色体.每一个染色体都代表着问题的一种解决方案.对群体的个体按照它们对环境适应度施加一定的操作,从而实现优胜劣汰的进化过程.从优化搜索的角度而言,遗传操作可以使问题一步一步接近最优解.用整数字符串代表染色体是展现飞机与登机口关系的一个简单方式.字符串的长度和每一个字符都与一架飞机相联系,同时基因里的特殊数字代表着这架飞机分配的登机口.比如,字符串6314542表示成功安排7架飞机到6个停机位,飞机4和6都被分配到停机位4. 1)适应度函数 在前文中提到过遗传算法在开始阶段会随机产生一个初始种群,然后对初始种群的每条染色体进行评价,留下适应度高的个体,低的被淘汰,再按照交叉概率和规则进行交叉操作,对于新产生的个体计算其适应度值,同样留下适应度值高的个体最后进行变异操作,就这样一代代的遗传优良的基因个体,这样逐步朝着更优解的方向进化.在这个过程中适应度值的计算是根据适应度函数来决定的,设定适应度函数为:fitness f=1/Z.适应度值越大,所求的目标函数值越小. 2)选择方式 遗传算法中适应性强的染色体就会有更大的机会被选择.选择两个染色体,进行交叉、变异得到下一代.重复这个过程多次,得到一个新的染色体.通过阻止好的染色体在交叉变异过程中被破坏,一些最好的染色体替代那些后代中最坏的染色体.当然,最好染色体的数量是比较小的,这样可以防止它们主导整个选择的过程.选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代.种群中的个体的适应度值是根据适应度函数决定的,在算法进行过程中会一直面临选择的问题,选择适应度值高的个体进行交叉操作,进行变异操作,所以都是通过选择来使得好的解或者个体能够被留下来进行下一步操作,在这里用常见的轮盘赌选择方法,来根据适应度值的大小来进行选择. 交叉:交叉是指把两个父代个体的部分结构加以替换重组而生成新的个体,本文主要用的是单点交叉法.具体操作是:在个体串中随机设定一个交叉点,实行交叉时,该点前或后的两个个体的部分结构进行互换,并生成两个新个体.这样产生的子代可能是不可行的,所以需要不断的检查和修改,比如选择了一个交叉点i(对应航班号),在其之前的基因都是可行的,就需要从i+1开始检查,首先要确定当前的停机位分配状况,如果可行就转到下一个基因,如果不可以就需要重新分配然后在转到下一个基因. 变异:对群体中的个体串的某些基因的基因值作一个变动,一般来说,变异操作的基本步骤如下:对群中所有个体以事先设定的变异概率判断是否进行变异,然后对进行变异的个体随机选择变异位进行变异. 现将上述模型应用于某机场的停机位分配.因为机场运作是一个连续不断的过程,在此为了寻找一个全局最优解,截取其中一段时间,该机场现有10个停机位可用,有34个航班在9∶00~18∶00时间内需分配停机位,每个机位的开放时间都是9点,结束都是18点,具体计划信息见表1. 表1 部分进、离港航班时刻表 遗传算法参数设定值如下:群体规模:20;交叉概率0.9;变异概率:0.05;最大进化代数:200;运用MATLAB进行计算求解. 根据原计划得到的停机位的分配甘特图如图1所示,通过运用数学模型的严格约束之后得到的停机位分配甘特图如图2所示. 图1展示了无安全条件下的机场停机位分配结果,图2展示了考虑安全因素的停机位分配结果.根据测试结果,从图1中可以看出,在135时刻和192时刻左右,对于停机位9和10来说,地面运动时间的重叠性很高,航班6在135时刻要离港,而航班10在136时刻需要降落滑行进港,同样在192时刻航班10要离港而在193时刻航班17需要进港,而且被分配在相邻的停机位9和10,这样就会在滑道上相遇,这种冲突必然就会导致一些航班无法正常进港或者离港,带来不必要的延误,也具有一定的潜在危险性,所以在实际情况中这种事不合理的分配.同样,在图中也可以看到其他的一些航班,其抵达时间和离开时间的重叠性,可以看出冲突有时会发生在航班18和23,10和17,23和27,31和34等. 图2的结果可以看出通过加入严格的约束,控制每个机位航班的进出时间间隔,可以尽量避免停靠在相邻停机位的航班冲突,将两个进离港时刻非常接近的航班安排在不相邻的停机位上.对于地面活动重叠性高的航班,任意两架飞机都不能安排到相邻的停机位,这样可以尽量减少因为地面活动时间冲突带来的延误.图3的结果可以地面活动重叠性高的航班,任意两架飞机都不能安排到相邻的停机位.可以看出由于这个限制,很多其他航班的停机位分配也变得不同.随着迭代次数的增加,群体值对应的曲线在迅速下降.而且,解决方案显示,经过大概10次迭代,收敛性更强. 图1 原计划停机位分配甘特图Fig.1 Gate assignment information ganntt chart under original plan 图2 优化后停机位分配甘特图Fig.2 Stands assignment information ganntt chart after optimizing 图3 优化结果输出Fig.3 Output the results of optimization 在总结国内外对于停机位分配的研究的基础上,确定停机位分配问题的要求和目标,考虑航班地面活动,合理分配各停机位空闲时间,建立了避免冲突的停机位分配模型.结合实例.运用MATLAB编程软件对模型进行求解,验证了模型的有效性,结果显示模型可以很好的避免在单跑道的机场出现航班滑行冲突的问题.但是停机位分配问题是一个复杂的多目标多约束问题,考虑其他目标或约束条件,进一步的优化是未来的研究方向. [1] 乐美龙, 檀财茂. 非正常运行下机场停机位实时分配模型[J].工业工程, 2014, 17(1):12-16. [2] 王志清, 商红岩, 宁宣熙. 机场登机口优化调度算法及实证[J].南京航空航天大学学报(自然科学版), 2007, 39(6):819-823. [3] 陈 欣, 陆 迅, 朱金福. 停机位指派模型的排序模拟退火算法[J].应用科学报, 2010, 25(5):520-525. [4] 杨文东, 朱金福, 许 俐. 基于航班连接树的机场停机位指派问题的研究[J]. 山东大学学报(工学版), 2010, 40(2):153-158. [5] TANG C H, YAN S H, HOU Y Z. A gate reassignment framework for real time flight delays[J].Springer-Verlag. 2010, 8(3):299-318. [6] 冯 程, 胡明华, 赵 征. 一种新的停机位分配优化模型[J].交通运输系统工程与信息. 2012, 12(1):131-138. [7] 李军会, 朱金福, 高 强. 基于贪婪禁忌算法的停机位指派问题研究[J].交通运输系统工程与信息, 2011, 11(4):173-179. [8] WANG H W, LUO Y X, SHI Z J. Real-time gate reassignment based on flight delay feature in hub airport[J].Mathematical Problems in Engineering,2013(3):1-10. [9] DORNDORFA U, DREXLB A. Flight gate schedulingState-of-the-art and recentdevelopments[J]. Omega,2007(35):326-334. [10] CHENG C H, HO S C, KWAN C L. The use of meta-heuristics for airport gate assignment[J]. Expert Systems with Applications, 2012, 39:12430-12437. Based on the research of security constraints of airport gate assignment CHEN Qian, LE Meilong (Scientific Research Academy, Shanghai Maritime University, Shanghai 201306) Gate plays a key role in the airport operation system. Without a reasonable and efficient gate assignment, the flights will not arrive at the scheduled gates on time according to the original plan. As the rising number of the flights, it’s a great challenge to enhance the efficiency of the airport operations, which requires rational allocation of gates. Meanwhile, reasonable control on idle time of the various gates is conducive to avoid the potential conflicts between adjacent gates. Considering the safety, the gate assignment model is established to avoid the conflicts and applied into the practice. The Gantt chart about the gate assignment demonstrates that the model is reasonable, efficient and more realistic indicating the improve on the operation efficiency of the airport. air transportation management; gate assignment; efficiency; safety operation; genetic algorithm 2015-05-17. 国家自然科学基金项目(71471110). 1000-1190(2016)01-0055-06 U8 A *E-mail: chenqian181@126.com.
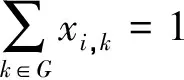

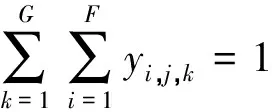
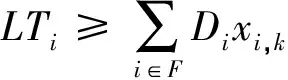
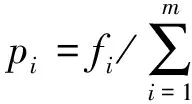
2 实例分析


3 小结

