混合候鸟迁徙优化算法求解柔性作业车间调度问题

姚 妮

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)



混合候鸟迁徙优化算法求解柔性作业车间调度问题

姚 妮*

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)

将基本候鸟迁徙优化(Migrating birds optimization， MBO)算法与变邻域搜索策略相结合，提出了一种混合候鸟迁徙优化(Hybrid migrating birds optimization， HMBO)算法求解以最小化最大完工时间为目标的柔性作业车间调度问题(Flexible job shop scheduling problem， FJSP).首先，给出了两段式编码/解码方式.为了保证初始解的质量和多样性，设计了一种两阶段种群初始化方法；其次，引入了一种个体重置机制，以避免算法陷入局部最优解.根据FJSP问题的特点，采用3种邻域结构用于构造个体邻域解，并以此为基础设计了一种变邻域搜索算法，增强算法的局部搜索能力.最后，通过基准算例测试了算法的性能，实验数据验证了本文算法在求解FJSP问题方面的有效性.

柔性作业车间调度； 最大完工时间； 候鸟迁徙优化算法； 变邻域搜索策略

柔性作业车间调度问题(Flexible job shop scheduling problem， FJSP)比经典作业车间调度问题(Job shop scheduling problem， JSP)更为复杂，前者是后者的一个扩展形式，已被证明具有NP难的特性[1].与JSP问题相比，FJSP问题中减少了机器约束，增加了调度的灵活性，这使其能够更贴近于实际的生产[2].

目前已有很多学者对FJSP问题进行了积极的探索和研究，并取得了大量的成果.近几十年来国内外很多学者采用智能优化算法对FJSP问题进行了研究，为FJSP问题的求解提供了新的思路和方法.Kacem等[3-4]针对多目标FJSP问题采用遗传算法进行求解，使车间内工件的最大完工时间、机器总负载以及关键机负载最小.Brandimarte[5]基于禁忌搜索算法对FJSP问题进行了研究.Xing等[6]将知识模型和蚁群算法有效结合，提出了一种基于知识的蚁群算法求解FJSP问题.Ziaee[7]提出了一种高效的启发式算法求解以最大完工时间为目标的FJSP问题.贺仁杰等[8]提出了一种知识型协同演化方法对FJSP问题进行求解.各种群采用不同进化方法和参数设置，通过种群间的资源竞争和信息共享向前推动算法的进化过程.Rahmati和Zandieh[9]将生物地理学算法应用于FJSP问题的求解，并通过与遗传算法的比较验证了算法的有效性.

近些年，随着智能优化算法的迅速发展，出现了模拟自然界候鸟迁徙行为的候鸟迁徙优化(Migrating birds optimization， MBO)算法[10].目前国内外学者已将MBO算法成功运用于生产调度问题的求解[11-13]，但这些研究多集中于流水车间内的调度问题.因此，本文在基本候鸟迁徙优化算法的基础上进行一系列改进，提出了适用于FJSP问题的混合型候鸟迁徙优化(Hybrid migrating birds optimization， HMBO)算法.采用两阶段种群初始化方法，引入个体重置机制，设计三种邻域结构用于构造个体的邻域解，并在算法中嵌入变邻域搜索策略进一步增强局部寻优能力.通过基准算例测试了算法的性能，并验证了其有效性.

1 柔性作业车间调度问题

FJSP问题可描述为：车间内n个工件在m台机器上加工.各工件均包含一道或多道工序，同工件各工序间存在固定的加工顺序.工序可在多于一台的机器上加工，其加工时间与所在机器有关.FJSP问题优化的目标是为工序分配适当的机器，排列各机器上工序间的加工顺序并计算其开始/完工时间，最终使系统某个或某些性能达到最优[1].

对于这样的系统，存在一些基本的假设条件：

1)初始零时刻所有工件和机器都是可用的.

2)一台机器在某一时刻只允许加工一个工件.

3)各工序的加工过程一旦开始不允许被中断.

4)同工件工序间具有先后加工的约束关系，不同工件工序间则相互独立.

5)各工件具有相同的加工优先级.

6)忽略机器加工工序前所需的调整时间.

高效快速完成生产任务仍然是大多数企业追求的首要目标.因此，本文以最大完工时间Cmax作为优化目标，则目标函数可表示为

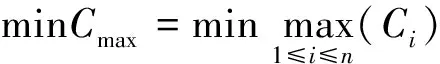
其中，Ci表示工件i的完工时间.

2 混合型候鸟迁徙优化算法

候鸟迁徙优化算法是一种新兴的邻域搜索技术，它通过模拟候鸟的自然迁徙行为来实现对目标的优化[10].整个算法分为算法初始化，领飞鸟进化，跟飞鸟进化和领飞鸟替换四个阶段.种群中所有个体构成V字形编队，由领飞鸟开始向队列两端通过搜索个体的邻域解进行进化，最终实现目标的优化.种群中的个体除了搜索自身邻域解进行更新外，还可以搜索其所在队列中前一个个体的邻域解(领飞鸟除外，只搜索自身邻域解).这种搜索机制能够提高算法找到更优解的概率，使算法能够快速地获得最优解，体现了算法的集中搜索能力[13].MBO算法比较适用于求解离散组合优化问题[13]，因此，本文针对FJSP问题的特点采取一系列改进措施，使MBO算法能够更好地用于FJSP问题的求解.

2.1 编码/解码方案

由于求解FJSP问题主要是解决机器分配和工序排序两个子问题，因此种群中每个个体可分为两段表示，长度均为车间内的工序总数.前半段表示机器分配方案，后半段表示工序间排序方案，如图1所示.前半段中元素值为工序所在机器的编号，按固定顺序存储，如图1(a)所示；后半段中相同的元素值表示同一工件的不同工序，元素间的先后顺序表示工序间的加工顺序，如图1(b)所示.

解码时结合前后两段编码进行操作，从左到右依次读取后半段元素代表的工序，然后在前半段找到其对应的机器，并计算工序的开始和完工时间.

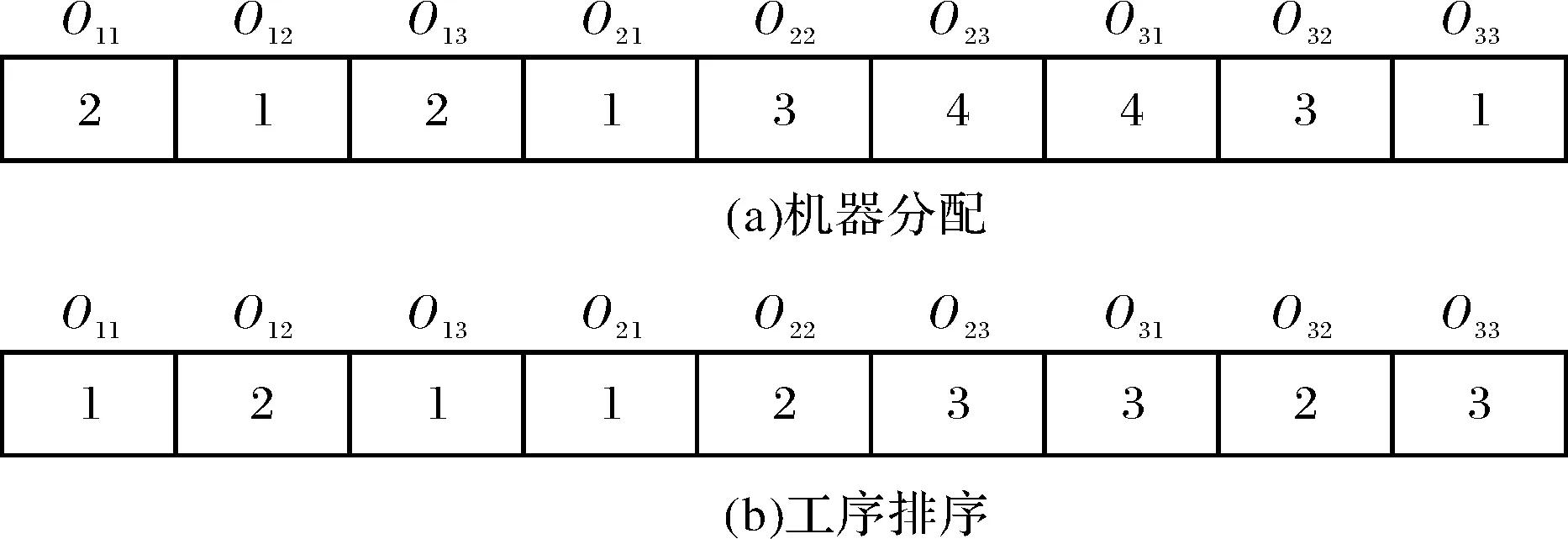
图1 编码方案Fig.1 The encoding scheme

2.2 种群初始化方案

与其他群智能优化算法(如遗传算法和粒子群算法等)相同，候鸟迁徙优化算法的性能也在一定程度上受到种群初始解的影响.因此，设计一个好的种群初始化方案是必须要解决的问题.根据个体编码方式，初始种群可分两个阶段进行初始化，即机器分配阶段和工序排序阶段.

对于机器分配阶段，采用以下3种方法：

1) 随机生成法：在每道工序可加工机器集内随机选择一台机器填入初始解的前半段.

2) 全局搜索法：采用文献[2]中的全局搜索方法确定初始解前半段机器分配方案，使机器的工作负载平衡，提高机器的使用率，并同时考虑最小化最大完工时间.

3) 局部搜索法：采用文献[2]中的局部搜索方法确定初始解前半段机器分配方案，其目的和全局搜索方法一样.

对于工序排序阶段，目前很多文献均采用随机生成法或根据调度规则生成初始排序方案[14-15].本文采用基于搜索的方法得到初始解的后半段.针对每一个已生成的机器分配方案，均采取以下操作：首先随机生成若干个工序排序方案，然后评估每个排序方案结合该机器分配方案后各自对应的目标值，选择其中最优的一组作为初始解.

2.3 邻域结构

候鸟迁徙优化算法中个体通过搜索自身以及排前一个个体的邻域解对问题的解空间进行搜索，以获取优化目标的最优值.因此，邻域解的构造直接影响着算法的求解质量和收敛速度.本文采用以下3种邻域结构，具体构造过程如下：

1) 邻域结构N1：在调度解的工序排序部分任意选择两个位置，并将两位置间元素逆序排列.

2) 邻域结构N2：在调度解的工序排序部分任意选择两道不同工件的工序，并互换两工序所在的位置.

3) 邻域结构N3：在调度解的机器分配部分任意选择一道工序，并将其分配至可选机器集合中(不包括当前机器)加工时间最短的机器上.

2.4 重置机制

在算法中引入一种重置机制，以避免算法陷入局部最优解.具体做法为，首先为种群中每个个体均设置一个解龄.对于新产生的个体，其解龄为1，若经过一次进化后计算结果未发生变化的个体，其解龄加1.若某个个体的解龄超过了预定的上限limit，则对该个体进行重置操作，即采用上述全局搜索法和基于搜索的方法重新生成一个新个体替代原来的个体.

2.5 变邻域搜索

基于上述3种邻域结构设计一种变邻域搜索算法嵌入到候鸟迁徙优化算法中，并作用于当前最优个体，以加强算法的局部搜索能力.

变邻域搜索算法的具体步骤如下：

步骤1：算法初始化.将候鸟迁徙优化算法得到的当前最优解作为变邻域搜索算法的初始解π，设置qmax←3，it←1及最大循环次数itmax.

步骤2：设置q←1.

步骤3：振动环节.若q=1，则按邻域结构N1和N3对π进行变换得到新解π′；若q=2，则按邻域结构N2和N3对π进行变换得到新解π′；若q=3，则按邻域结构N3对π进行变换得到新解π′.

步骤4：局部搜索.以振动环节得到的π′作为局部搜索的初始解，找到局部最优解π″.

步骤5：若π″优于π，则π←π″，并设置q←1；否则，设置q←q+1.

步骤6：判断q>qmax是否成立.若是，设置it←it+1，执行步骤7；否则，转到步骤3.

步骤7：判断it>itmax是否成立.若是，执行步骤8；否则，转到步骤2.

步骤8：变邻域搜索结束.

变邻域搜索算法中局部搜索的具体步骤如下：

步骤1：获取初始解π′，并设置lmax←3，λ←1和最大循环次数λmax.

步骤2：设置πL.

步骤5：判断l>lmax是否成立.若是，则设置λ←λ+1，执行步骤6；否则，转到步骤3.

步骤6：判断λ>λmax是否成立.若是，π″←π′，并执行步骤7；否则，转到步骤2.

步骤7：局部搜索结束.

2.6 HMBO算法步骤

HMBO算法具体步骤如下：

步骤1：设置算法参数及终止条件Kmax，并令K←1，g←1，fg←1.

步骤2：按照2.2节的方法生成算法初始种群.

步骤3：领飞鸟进化.根据三种邻域结构产生领飞鸟k′个邻域解，若其中的最优解优于当前领飞鸟，则替换领飞鸟，并将其余本次进化未用到的x个最好的邻域解同时加入共享邻域解集SL和SR中.

步骤4：左队列跟飞鸟进化.对于左队列中每个个体πL，根据邻域结构产生自身k′-x个邻域解，并构成集合NL.若NL∪SL中的最优解优于当前解πL，则替换πL.置空SL，将NL∪SL中本次进化未用到的x个最好解加入SL.

步骤5：右队列跟飞鸟进化.对于右队列中每个个体πR，根据邻域结构产生自身k′-x个邻域解，并构成集合NR.若NR∪SR中的最优解优于当前解πR，则替换πR.置空SR，将NR∪SR中本次进化未用到的x个最好解加入SR.

步骤6：更新当前最优解.

步骤7：更新每个个体的解龄.

步骤8：令g←g+1，并判断是否满足g>G.若是，则令g←1，并执行步骤9；否则，转到步骤3.

步骤9：检查每个个体的解龄.若超过limit，则对其执行重置操作.

步骤10：更新当前最优解，并对其执行变邻域搜索，将产生的新解替换当前种群中最差解.

步骤11：替换领飞鸟.若fg=1，左队列中第一个个体作为新的领飞鸟，将领飞鸟移至左队列末端，并设置fg=0；否则，右队列中第一个个体作为新的领飞鸟，将领飞鸟移至右队列末端，并设置fg=1.

步骤12：令K←K+1，判断是否满足K>Kmax.若是，则转到步骤13；否则，执行步骤3.

步骤13：算法结束.

3 仿真实验

本节针对文献[3-5]中柔性作业车间调度问题的15个基准算例(Kacem01～Kacem05和MK01～MK10)对HMBO算法的性能进行测试.采用Fortran语言编程，程序在WinXP系统下内存4G的Intel Core (TM) i5-2400 CPU 3.10GHz的计算机上运行.算法中4种参数根据文献[10]推荐的数值进行设置，即种群规模51，个体搜索邻域解个数k′=3，共享邻域解个数x=1，巡回次数G=10.此外，通过大量实验设置解龄上限limit=10，最大循环次数Kmax=500，itmax=30，λmax=10.

为了避免算法陷入局部最优解，HMBO算法中引入了一种个体重置机制.因此，这里首先对个体重置机制的有效性进行验证.将排除个体重置机制后得到的算法HMBO1与HMBO算法进行比较，对比结果如表1所示.表中n×m表示算例问题的规模，两种算法分别针对15个不同算例独立运行10次并取平均值.由表中数据可以看出，HMBO算法的结果明显优于HMBO1算法的结果.

为了进一步验证HMBO算法的有效性，将其与文献[4-8]中5种算法进行比较，对比情况如表2和表3所示，其中符号‘-’表示文献中未给出相应的数据，黑体表示各算法经对比后的最佳结果.表2中第2～6列给出了由各文献提供的算法在计算各算例时的最优值，第7列为本文算法得到的最优结果.由表1可以看出，本文HMBO算法只在算例Kacem05略差于文献[6]和文献[8]中的算法，且只相差一个时间单位.表3中针对Brandimarte算例进行了进一步地比较和分析.首先给出各算法在计算相应算例时得到的最优值，然后计算其相对百分比偏差值(Relative percent deviation， RPD).计算公式为

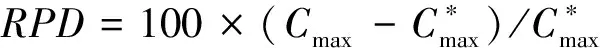
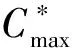
献[6,8-9]中的算法均能在10个算例中得到6个算例的最佳结果，但是本文算法得到的平均相对百分比偏差RPD的数值最小.因此，本文提出的HMBO算法具有一定的有效性.

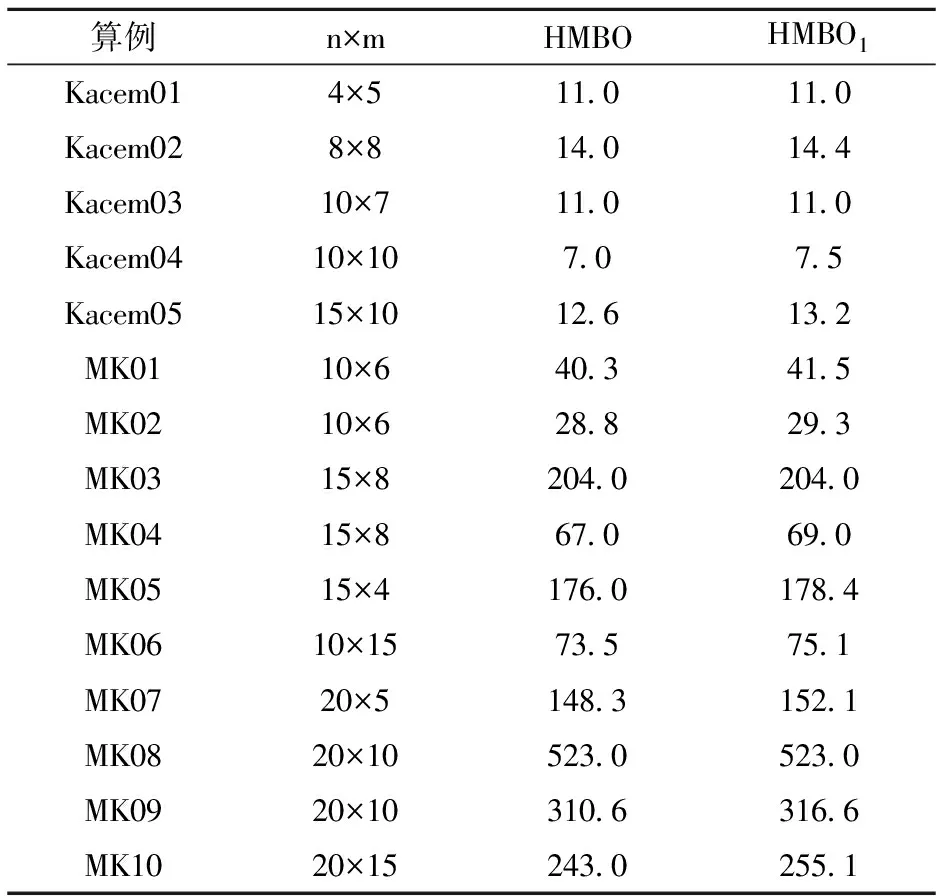
表1 两种算法对比结果

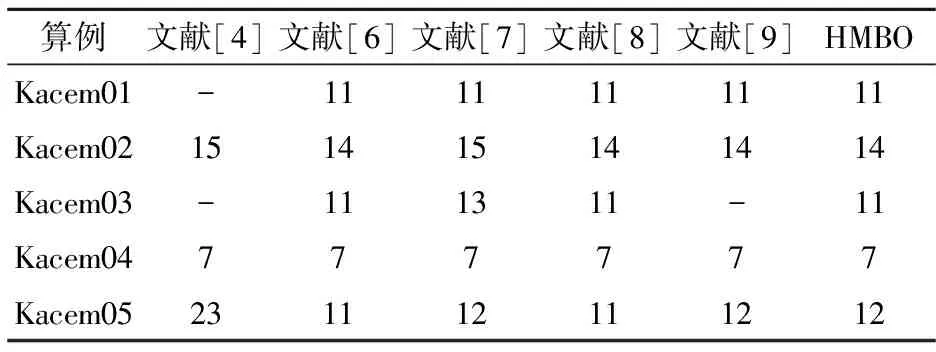
表2 Kacem算例对比结果

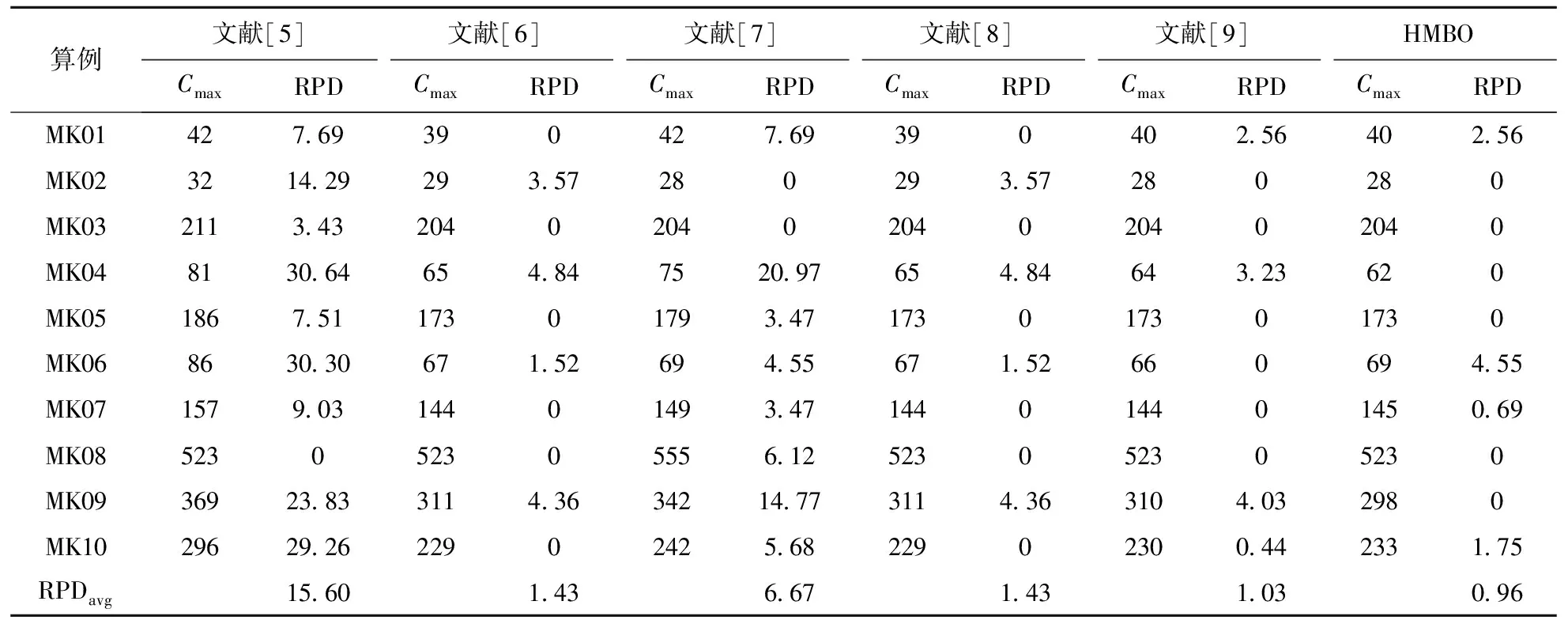
表3 Brandimarte算例对比结果

4 结论

本文针对FJSP问题，以最小化最大完工时间为目标，结合基本候鸟迁徙优化算法和变邻域搜索算法，提出了适用于FJSP问题求解的混合型候鸟迁徙优化算法.该算法采用两阶段种群初始化方案，保证了初始种群质量和多样性；设计了个体重置机制，以避免算法陷入局部最优解；针对每个个体，设计了3种邻域结构用于构造个体邻域解；设计变邻域搜索算法并嵌入到候鸟迁徙优化算法中，增强了算法的局部搜索能力.通过对基准算例的计算，验证了HMBO算法在求解FJSP问题方面的有效性.

目前候鸟迁徙优化算法在求解生产调度问题方面的研究仍处于起步阶段，下一步工作需将算法推广到其他更复杂的车间调度问题中，并结合问题的特点，设计出更加高效的算法.

[1] 张超勇， 饶运清， 李培根， 等. 柔性作业车间调度问题的两级遗传算法[J]. 机械工程学报， 2007， 43(4): 119-124．

[2] 张国辉， 高 亮， 李培根， 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报， 2009， 45(7): 145-151．

[3] KACEM I， HAMMADI S， BORNE P. Pareto-optimality approach for flexible job-shop scheduling problems: hybridization of evolutionary algorithms and fuzzy logic[J]. Mathematics and Computers in Simulation， 2002， 60(3): 245-276.

[4] KACEM I， HAMMADI S， BORNE P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part C: Applications and Reviews， 2002， 32(1): 1-13.

[5] BRANDIMARTE P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of Operations Research， 1993， 41(3): 157-183．

[6] XING L N， CHEN Y W， WANG P， et al. A knowledge-based ant colony optimization for flexible job shop scheduling problems[J]. Applied Soft Computing， 2010， 10(3): 888-896.

[7] ZIAEE M. A heuristic algorithm for solving flexible job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology， 2014， 71(1-4): 519-528．

[8] 贺仁杰， 陈宇宁， 姚 锋， 等. 求解柔性车间作业调度的知识型协同演化方法[J]. 计算机集成制造系统， 2011， 17(2): 310-315．

[9] RAHMATI S H A， ZANDIEH M. A new biogeography-based optimization (BBO) algorithm for the flexible job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology， 2012， 58(9-12): 1115-1129．

[10] DUMAN E， UYSAL M， ALKAYA A F. Migrating birds optimization: a new metaheuristic approach and its performance on quadratic assignment problem[J]. Information Sciences， 2012， 217: 65-77．

[11] PAN Q K， DONG Y. An improved migrating birds optimisation for a hybrid flowshop scheduling with total flowtime minimisation[J]. Information Sciences， 2014， 277: 643-655．

[12] TONGUR V， ÜLKER E. Migrating birds optimization for flow shop sequencing problem[J]. Journal of Computer and Communications， 2014， 2(4): 142-147．

[13] 谢展鹏， 贾 艳， 张超勇， 等. 基于候鸟优化算法的阻塞流水车间调度问题研究[J]. 计算机集成制造系统， 2015， 21(8): 2099-2107．

[14] PEZZELLA F， MORGANTI G， CIASCHETTI， G. A genetic algorithm for the flexible job-shop scheduling problem[J]. Computers &Operations Research， 2008， 35(10): 3202-3212．

[15] GAO K Z， SUGANTHAN P N， PAN Q K， et al. Discrete harmony search algorithm for flexible job shop scheduling problem with multiple objectives[J]. Journal of Intelligent Manufacturing， 2015， 26(12):1-9．

Hybrid migrating brids optimization algorithm for the flexible job shop scheduling problem

YAO Ni

(School of Computer and Communication Engineering， Zhengzhou University of Light Industry， Zhengzhou 450002)

In this paper， a hybrid migrating birds optimization algorithm (HMBO) is proposed to solve the flexible job shop scheduling problem (FJSP) with the objective of minimizing the makespan by combining the basic migrating birds optimization (MBO) and the variable neighborhood search strategy. Firstly， two-phase encoding and decodingapproaches are given， and a two-stage population initialization method is developed to ensure the quality and diversity of initial solutions. Secondly， an individual reset mechanism is introduced to avoid the algorithm being trapped into the local extremum. In terms of the features of the FJSP， three neighborhood structures are adopted to generate individual neighboring solutions， and based on which a variable neighborhood search algorithm is designed to enhance the local searching capability of the algorithm. Finally， some benchmark instances are used to test the performance of the algorithm. Experimental data show that the proposed algorithm is effective for solving the FJSP．

flexible job shop scheduling； makespan； migrating birds optimization algorithm； variable neighborhood search strategy

2015-07-25.

河南省科技攻关项目(122102210492)．

1000-1190(2016)01-0038-05

TP18

A

*E-mail: zzulijsjyn@163.com．