弱束缚三体离子原子体系Li+-4He2的能级和结构

刘 敏 敏

(武汉工程大学 理学院， 武汉 430205)



弱束缚三体离子原子体系Li+-4He2的能级和结构

刘 敏 敏*

(武汉工程大学 理学院， 武汉 430205)

采用耦合道超球坐标方法和B样条函数系统细致地研究了Li+-4He2体系束缚能级和结构，计算了体系的基态束缚能和结构以及部分激发态的束缚能量，获得了较高精度的基态能量和结构参数，并首次报道了部分激发态的束缚能.通过研究极化修正项的作用，发现三体极化修正项对系统的能量和结构都有着细小的影响，使得束缚能量比没有考虑其时更低，能量大约变化1%，使得基态的结构更加扁平，即其使得体系束缚的更为紧密.

弱束缚； 束缚能； 结构； 极化

近年来，离子和氦原子之间的微弱相互作用引起了实验和理论上的广泛关注[1-13].实验表明，氦原子液滴可以和一个碱金属阳离子形成Li-Hen和Li+-Hen(n=1，2，3，4，…)等结构[14].这些新形成的离子分子的结构和形成成为了实验和理论关注的焦点.对于Li+-He两体系统，它们之间的相互作用势已经有相关的文献进行了报道，在此基础上，理论上可以用合适的计算方法研究Li+-Hen体系的束缚能与结构特征[15-20]，而且是研究多体Li+-Hen(n=3，4，…)的基础.

目前对Li+-Hen体系的研究多集中在探讨Li+在氦原子簇中的位置以及体系中氦原子的数目有多少上，但是对于小分子体系Li+-He2的研究相对较少，而且未发现有对其激发态的研究.迄今为止，只有2005年C. D. Paola小组通过离散高斯方法(Distributed Gaussian Functions Method，DFG)和量子蒙特卡洛方法(Diffusion Monte Carlo method，DMC)计算和报道了Li+-He2体系的基态能为E0=-1041.7cm-1[18]；2006年F.Sebastianelli小组通过Hartree-Fock(Ab initio post-Hartree-Fock method，HF)从头计算方法报道了Li+-He2体系的结构为RHeHe=5.61和RLi+He=3.61[19]；此外在2007年，E.Coccia， F. A.Gianturco等利用蒙特-卡洛方法(Monta Carlo Method，MCM)计算了Li+-4He2体系的束缚能和结构[20].在这些研究中，体系的相互作用势全都采用了两体势对加而没有考虑到三个离子之间的相互作用修正项，然而相互作用势的准确和精确性直接影响计算结果，因此有必要考虑极化修正项的影响，进一步获得更为准确的结果.而且，对于上述文献中的能量和结构结果没有其他的理论结果去验证其精准性，文献[18-20]中关于Li+-He2体系的结构所报道的结果并不完全一致，仅有一位有效数字相同.因此为了获得更为准确的结果需要采用新的研究方法和新的更准确的体系相互作用势，对Li+-He2体系的束缚能和结构更细致的研究是有必要的.

本文将采用耦合道超球坐标方法系统地研究Li+-4He2体系的能级和结构.耦合道超球坐标结合B样条方法由韩慧丽等人所建立，利用离散变量表示将耦合微分方程转化为解广义本征的问题，被成功地应用在弱束缚三原子体系的研究中[21-22].本文的主要的目的之一是将其推广应用到包含碱金属阳离子的弱束缚体系.同时本文为了与其他的计算结果相互比较，首先也采用两体对加势近似表达Li+-4He2体系的相互作用势，而后在两体对加近似势的基础上加上三体相互作用极化修正项来计算体系的束缚态物理量，通过比较进而获得三体极化修正项对此类体系能级和结构的影响.在两体势函数的选取上，本文选取Soldan等[23]报道的Li+-He体系的两体相互作用势，这是通过计算给出的一种由高精度计算后拟合所获得的解析表达形式，以及采Aziz等[24]报道的目前为止几乎最为真实准确的He-He两体势.另外本文也研究了Li+-4He2体系部分激发态的能级的结果.

1 理论方法

图1 Li+-4He2体系几何结构示意图Fig.1 Geometry construction of Li+-4He2 system

体系的薛定谔方程可写为：

R2Eψ(R，φ，θ),

(1)

式中，

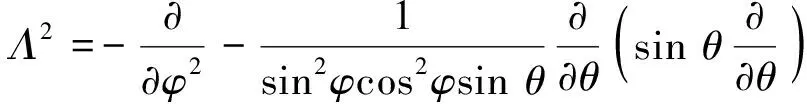
(2)

首先解绝热势方程：

φν(R，φ，θ)=Uνφν(R，φ，θ),

(3)

利用B样条函数构造道函数如下：

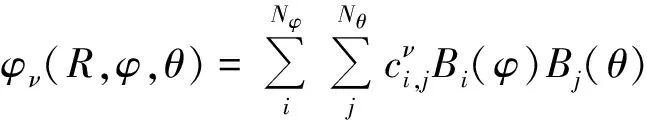
(4)

式中，Nφ，Nθ是φ和θ角向基组的数目.波函数径向函数和角向函数道函数构造如下[21-22]：

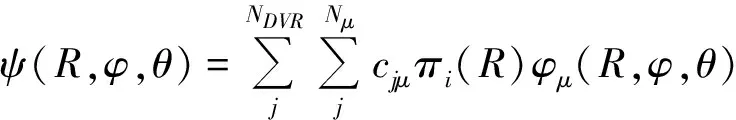
(5)

式中，NDVR，Nμ分别为离散变量基组数目和道函数数目，通过绝热超球近似，将超径看成是缓变量，通过离散变量法可以解薛定谔方程(1)[21-22].

薛定谔方程(1)中V(R，φ，θ)表示体系的相互作用势.在不考虑三体力的情况下，体系的总体相互作用势近似为：

Vad=VLi+-He(r13)+VLi+-He(r23)+VHe-He(r12).

(6)

同时由于Li+离子对He原子的极化作用，使得其形成电偶极子，而两个电偶极子之间也会相互作用，这样会改变体系的性质，原则上是不可以忽略的，因此我们进一步考虑了三体力对体系能级和结构的影响，这样三体系统的总相互作用势为：

Vf= VLi+-He(r13)+VLi+-He(r23)+

VHe-He(r12)+V3B,

(7)

式中，V3B为三体相互作用修正项，采用文献[25-26]中给出的形式，如下：

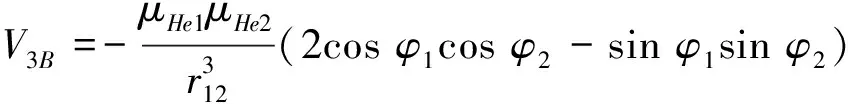
(8)

2 结果与分析

2.1 两体相互作用

图2 Li+-He体系和He-He体系两体相互作用势随两粒子之间的间距变化示意图Fig.2 The potential-energy curves of the Li+-He pairs and He-He trimer

图2是Li+-He、He-He两种体系的两体相互作用势的示意图，He-He体系的势放大了10倍.从图中可以看出Li+-He体系的势阱深度深，而势阱浅的是He-He体系.He与He之间为范德瓦尔斯势，相互作用较弱，Li+与He之间的相互作用主要为极化相互作用，比He与He的相互作用要强很多.采用这两种模型势计算，利用B样条函数直接对角化数值计算可以得到体系的束缚能.表.1是Li+-4He的所有束缚能级.与双原子体系相比较，此类离子与原子所构成的两体系统的束缚能明显不同，它们的束缚能级相对多.对于Li+-4He2体系，其基态束缚能为-502.84217 cm-1，对应角动量值J=0-17体系都存在着束缚能.

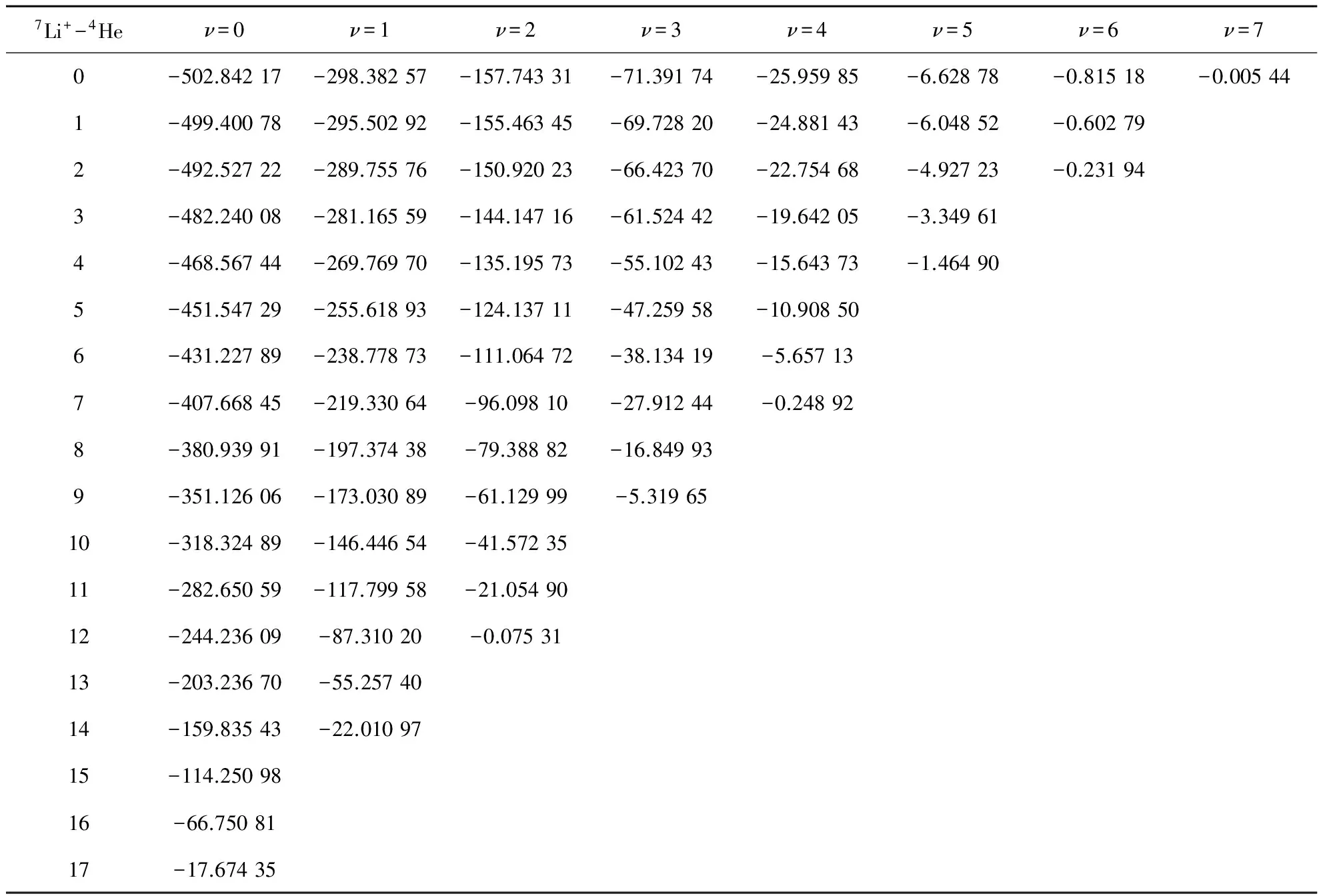
表1 7Li+-4He体系的振转能级

2.2 三体相互作用

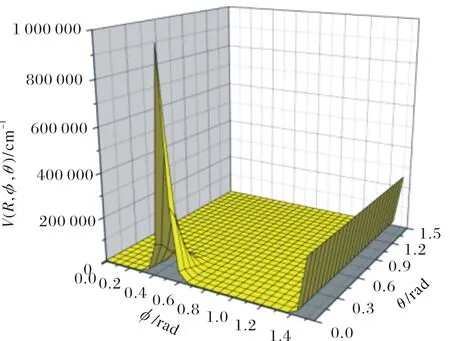
图3 Li+-4He2体系的相互作用随超径R，超角φ以及夹角θ变化的示意图Fig.3 The three-body interaction of Li+-4He2 system

2.2.2 超球势曲线 超球势计算得是否准确，精度是否合适对于体系能级和结构的计算精度有着直接的影响，因此我们首先对其做收敛性检验，保证后续的计算精度.表2列出了Li+-4He2体系的超球势的收敛情况.对于Li+-4He2体系，我们分别在短程和长程的超径R=6 a.u.(势阱)和R=20 a.u.(大超径)处进行了收敛性检验.从表中可以看出，当角向基矢取(Nθ，NΦ)=(80，135)时，势阱处的超球势有6～9位有效数字，而在大超径处至少有5～7位有效数字.在短程和长程位置的超球势曲线的收敛保证了后面计算结果的精确性.

表2 7Li+-4He2体系的超球势曲线的收敛性检验表

图4是Li+-4He2体系的绝热超球势曲线图.从图中可以看出，体系的超球势曲线均表现出强烈的反交叉，即此类体系的道间耦合较为强烈.在大超径处，超球势曲线逐渐趋向Li+-He两体体系的各束缚态能级，即Li+-He-He三体解离成两体Li+-He和一个自由的He原子.

2.2.3 基态束缚能与结构 表3列出了Li+-4He2体系基态的能级和结构参数随基矢(NDVR，Nμ)变化时的收敛性检验.〈r12〉，〈r13〉 和〈r23〉分别代表Li+-He和He-He距离的平均值.对于Li+-He2体系，基矢为(NDVR，Nμ)=(60，20)时，基态能量的计算结果有5位有效数字，〈r13〉，〈r12〉 和R分别有4位，4位和5位有效数字，cosφ3有四位有效数字，即φ3的平均值也有4位有效数字.

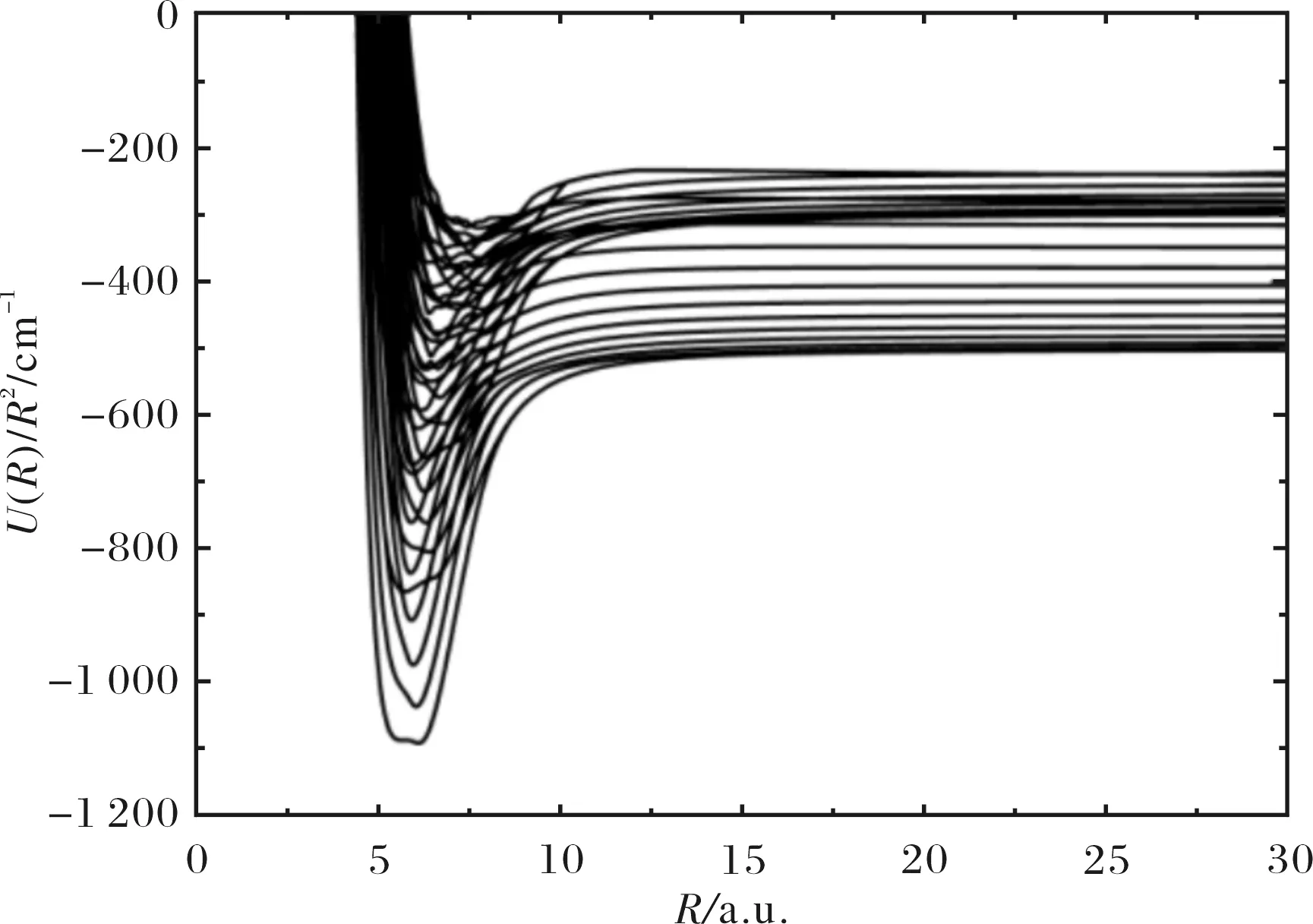
图4 Li+-4He2体系的超球势曲线图Fig.4 The hyperspherical potential-energy curves of the Li+-4He2 system

(NDVR，Nμ)E0/cm-1〈r13〉〈r12〉cosφ3R(60，10)-1006403746765975-0565760278(60，20)-1007193744966032-0570460284(60，30)-1007243744866037-0570460284

表4为Li+-4He2体系的基态能量和结构参数平均值.Vad列代表体系的总相互作用势为两体对加近似的结果，而Vf列则代表体系的总相互作用势考虑了三体力V3B的结果.可以看出Li+-4He2体系Li+与He之间的距离小于He与He之间的距离，是扁平等腰三角形结构，且原子之间的间距大致上有这样的关系：r23≈r12+r13.从表中也可以看出，以Li+离子为顶点的角度值都为钝角，细小的差别表明了三体力的微小影响.三体力对Li+-He2体系的顶角φ3影响分别为1.887%，使得体系变得更加扁平.E0表示体系的基态能量，当考虑三体力时，体系的基态能量变得更低，即体系束缚变强，能量值的变化比例ΔE0/E0=0.97%， 接近1%.但是基态束缚能量因此而变化18.59 cm-1，虽然占比重小但是已经是一个可观的能量变化值.整体来说，极化修正项V3B所起的作用相对微弱.

表4 Li+-4He2体系基态的能级和结构期望值

2.2.4 激发态束缚能 Li+-He2体系第1到第7激发态的能级如表5所示，我们分别考虑了两体对加势和三体极化修正项的情形.可以看到，与基态束缚能类似，三体极化修正项改变了体系的激发态能量，使得激发态束缚比不考虑此项时更紧，对于越高的激发态，修正项所改变的束缚能量值越小.

表5 Li+-4He2体系激发态的能级

2.2.5 Li+-4He2体系的基态能量和结构参数平均值与其他结果的比较 表6列出了本文所计算的 Li+-He2体系的基态能量和结构参数平均值与其他结果.比较可以看到我们所计算的基态束缚能量与DFG和DVR方法[18]所计算的结果数值上相差近34 cm-1， 这是由于我们采用了拟合势计算的结果，但是在结构体系呈现等腰三角形结构且腰长近似相等，只是底边长度有所不同，这样对应的三角形以为Li+顶点的顶角数值也有微小的偏差.束缚能差别表明P.Soldan[23]等所给出的拟合势一定程度上符合其计算的势，但是并不能完全精确地表示其计算的精确势，若要更为精细的研究此体系，更为精确的拟合参数有待研究.HF方法[19]没有计算出体系的束缚能，与HF方法所计算的结果相比较，三角形的腰长接近但是底边长度相差较大.本文的结果与MCM的量子方法[20]结果相近，与其经典方法计算结果相差很大，说明其经典的计算结果不是很准确.相比较之下，我们的结果具有更高的有效数字和精度.

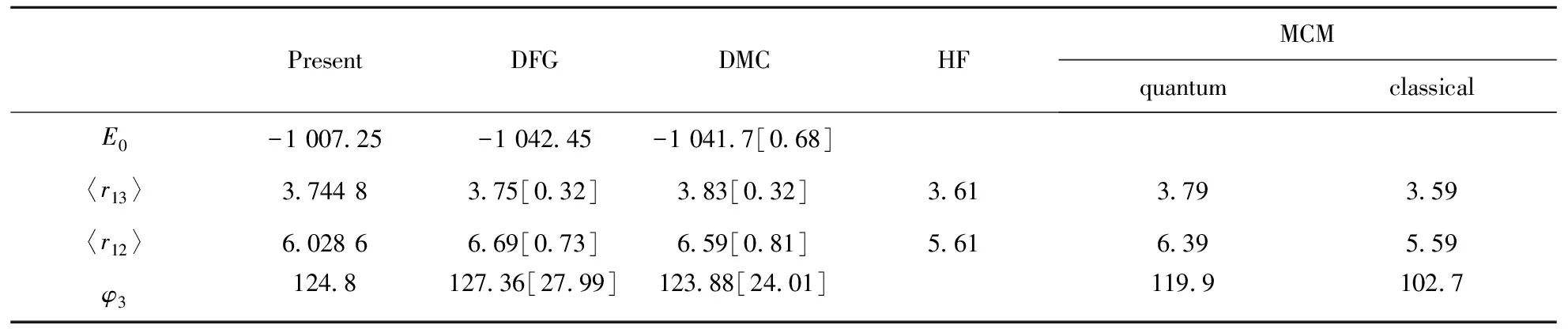
表6 Li+-4He2体系结果比较

3 结论

本文利用耦合道超球坐标结合B样条的方法研究了Li+-4He2体系的基态能级和结构以及部分激发态能量，发现Li+-4He2体系基态的结构呈现为等腰三角形.另外对于阳离子的三体系统Li+-4He2，三体相互作用修正项V3B对于它们束缚能与结构等物理量的平均值的影响被证明是很小的.也发现束缚能结果表明P.Soldan等所给出的拟合势一定程度上符合其计算的势.另外本文给出了更多有效数字和更为精度高的结果.

[1] DOERK H， IDZIASZEK Z， CALARCO T. Atom-ion quantum gate[J]. Phys Rev A， 2010， 81(1): 012708(1-4)．

[2] CETINA M， GRIER A， CAMPBELL J， et al. Bright source of cold ions for surface-electrode traps[J]. Phys Rev A， 2007， 76(4): 041401(1-4)．

[3] ZIPKES C， PALZER S， SIAS C， et al. A trapped single ion inside a Bose-Einstein condensate[J]. Nature， 2010， 464: 388-391．

[4] SCHMID S， HARTER A， DENSCHLAG J H. Dynamics of a Cold Trapped Ion in a Bose-Einstein Condensate[J]. Phys Rev Lett， 2010， 105(13): 133202(1-4)．

[5] KRYCH M， SKOMOROWSKI W， PAWLOWSKI F， et al. Sympathetic cooling of the Ba+ion by collisions with ultracold Rb atoms: Theoretical prospects[J]. Phys Rev A， 2011， 83(3): 032723(1-16)．

[6] STIENKEMIER F， HIGGINS J， ERNST W E， et al. Laser Spectroscopy of Alkali-doped Helium clusters[J]. Phys Rev Lett， 1995，74(18): 3592-3595．

[7] BISHOP D M， PIPIN J. Static electric properties of H and He[J]. Chem Phys Lett， 1995， 236(1-2): 15-18．

[8] LEZANA T G， SNEIRA J R， ARTES S M， et al. Efimov States for4He Trimers[J]. Phys Rev Lett， 1999， 82(8): 1648-1651．

[9] SUNO H. Adiabatic hyperspherical study of weakly bound He2H-1， He2H， and HeH2systems[J]. J Chem Phys， 2010， 132(22): 224311(1-10)．

[10] ROSSI M， VERONA M， GALLI D E， et al. Alkali and alkali-earth ions in4He systems[J]. Phys Rev B， 2004， 69(21): 212510(1-4)．

[11] IDZIASZEK Z， CALARCO T， ZOLLER P. Controlled collisions of a single atom and an ion guided by movable trapping potentials[J]. Phys Rev A， 2007， 76(3): 033409(1-16).

[12] D’INCAO J P， ESRY B D. Manifestations of the Efimov effect for three identical bosons[J]. Phys Rev A， 2005， 72(3): 032710(1-9)．

[13] BLUME D， ESRY B D， GREENE C H， et al. Formation of atomic tritium clusters and Bose-Einstein condensates[J]. Phys Rev Lett， 2002， 89(16): 163402(1-4)．

[14] LAN L A， BARTL P， LEIDLMAIR C， et al. Solvation of Na+， K+， and their dimers in Helium[J]. Chem Eur J， 2012， 18(14):4411-4418．

[15] SCHEIDMANN A A， KRESIN V V， HESS H. Capture of lithium by4He clusters: Surface adsorption， Penning ionization， and formation of He Li+[J]. J Chem Phys， 1997， 107(8):2839-2844．

[16] MARINETTI F， COCCIA E， BODO E， et al. Bosonic Helium clusters doped by alkali cations: interaction forces and analysis of their most stable structures[J]. Theor Chem Acc， 2007， 118(1): 53-65．

[17] MULLER S， MUDRICH M， STIENKEMEIER F. Alkali-Helium snowball complexes formed on helium nanodroplets[J]. J Chem Phys， 2009，131(4):044319(1-7)．

[18] PAOLA C D， SEBASTIANELLI F， BODO E， et al. Microsolvation of Li+in small He clusters. Li+Henspecies from classical and quantum calculations[J]. J Chem Theory Comput， 2005， 1(5):1045-1054．

[19] SEBSTIANELLI F， BODO E， BACCARELLI I， et al. Microsolvation of Li+in bosonic helium clusters. I. Many-body effects on the structures of the small aggregates[J]. Comp Mate Sci， 2006， 35(3):261-267．

[20] COCCIA E， BODO E， MARTINETTI F， et al. Bosonic helium droplets with cationic impurities: Onset of electrostriction and snowball effects from quantum calculations[J]. J Chem Phys， 2007， 126(12):124319(1-8)．

[21] HAN H L， LI Y， SHI T Y. The weakly bound states and resonances of the BeHe2triatomic system[J]. J Chem Phys， 2011， 134(19): 194307(1-7)．

[22] HAN H L， LI Y， ZHANG X Z， et al. Hyperspherical coupled channel calculations for the spectra and structure parameters of rare gas trimers NeAr2and Ne2Ar[J]. J Chem Phys， 2007， 127(15): 154104(1-9)．

[23] SOLDEN P， LEE E P F， LOZEILLE J， et al. High-quality interatomic potential for Li+He[J]. Chem Phys Lett， 2001， 343(3-4):429-436．

[24] AZIZ R A， SLAMAN M J. An examination of ab initio results for the helium potential energy curve[J]. J Chem Phys， 1991， 94(12): 8047-8053．

[25] ORLANDINI S， BACCARELLI I， GIANTURCO F A. Searching for many-body effects and Efimov states in very weakly bound triatomics: HeNeH-1and HeNeH[J]. Mol Phys， 2008， 106(2-4):573-586．

[26] STONE A J. The Theory of Intermolecular Force[M]. Oxford: Clarendon Press， 2013:43-47.

Energies and structure of weakly bound three-body Ion-atom Li+-4He2system

LIU Minmin

(School of Science， Wuhan Institute of Technology， Wuhan 430205)

The couple-channel hyperspherical method with B-spline function has been expanded to study the Li+-4He2system and demonstrated to be an effective and reliable method to study these weakly interacting ion-atomic three-body systems. Ground state energy and spatial features of these atom-atom-ion systems are investigated systematically together with bound energies of several excited states presented for the first time. The three-body polarization correction term， which is neglected in previous work， is taken into account for the interaction of the three particles in system. It is found that the contribution of three-body polarization correction on ground energies are subtle and make the system bind more tightly while the increments of ground energies are less than 1%. The polarization correction also make subtle modification in the geometric behaviors for these combinations．

weakly bound； bound energies； structure； polarization

2015-07-30.

湖北省教育厅科学研究计划指导性项目(B2015318)；武汉工程大学科学研究基金项目(K201422)．

1000-1190(2016)01-0043-06

O56

A

*E-mail: ocbmml@126.com．