基于35°Ahmed模型的外流场仿真精确性与 被动控制减阻研究

田 思， 谭文林， 张英朝， 吴 敏， 邵书鑫

(1. 奇瑞汽车股份有限公司， 安徽 芜湖 241000； 2.中国汽车工程研究院股份有限公司， 重庆 401120； 3.吉林大学 汽车仿真与控制国家重点实验室， 长春 130022)

计算流体动力学也被称作CFD[1]，它是用计算机数值计算去研究流体力学的一门学科，也是研究汽车空气动力学的一种手段。计算机技术的进步使得数值仿真的效率和仿真结果的可靠度都有了很大的提升[2]，尽管如此，要想得到地面车辆外流场的精确模拟依然不容易。车辆外流场的流动结构是很复杂的，而且气体的流动特征是不规则的，因此外流场仿真的精确度受很多因素的影响，主要有几何模型的前处理及建模、网格划分的类型、物理模型的选取、计算资源的供给和仿真策略的制定等[3]。在汽车CFD仿真分析中，我们主要研究汽车外流场，主要研究的对象为：应用快捷的CFD仿真方法来优化汽车的气动性能；为能够达到汽车气动性能的验证性要求，需要开发出准确度高的CFD仿真策略[4]。汽车的气动阻力主要由摩擦阻力和压差阻力组成[5]。湍流模型[6]、网格、求解器这3个影响因素对汽车外流场仿真精确性的影响至关重要。汽车尾部流场因气流分离严重而产生较复杂的湍流运动[7]，对这部分流场的仿真有一定的难度，也占用较大的计算资源。目前，应用较多的仿真方法有直接数值模拟、大涡模拟、雷诺时均法。不同的数值仿真方法对计算机硬件的要求也是不同的，在满足工程需要的前提下，本文选用常用的雷诺时均法进行仿真计算[8]，探索出一种质量高、精度高的CFD[9]仿真策略。雷诺时均法所用的模型包括Reynolds应力模型、标准k-e模型、Realizablek-e模型和SSTk-w模型等[9]。不同的仿真模型采用的求解方程不一样，也影响了计算结果的精确度，但基本都能满足工程需要。当采用数值方法求解控制方程时，都是想办法将控制方程在空间区域上进行离散，然后求解得到的离散方程组，要想在空间域上离散控制方程，必须使用网格。网格是离散的基础，网格节点是离散化后物理量的存储位置，网格在离散过程中起着关键的作用。网格类型[10]和布置对网格质量来说是至关重要的，常用的网格主要有4类，包括常用的四面体非结构网格和六面体剪切体网格，以及不常用的多面体非结构网格和十二面体剪切体网格。仿真的精确度受网格类型、网格尺寸和网格数量的影响很大[11]。本文要找到仿真精确度高的仿真策略，就要同时考虑湍流模型和网格对计算结果的影响，通过对不同组合的研究，得到最佳组合方案。Ahmed模型是研究外流场结构常用的一种类车体模型，它是由德国人Ahmed发明并提出的。通过试验，发现模型的阻力系数随着它的尾部倾角的变化而改变，且对应着不同的尾流结构。Ahmed等探究了该模型空气阻力的来源，这为后人研究减阻技术提供了极大的帮助。后人对Ahmed模型进行了大量的仿真与风洞试验，有丰富的经验数据可以参考。本文对汽车外流场仿真精确性的研究，采用35°Ahmed模型[12]，当尾部倾角为35°时，Ahmed模型阻力系数较低，且尾流结构稳定，适合进一步研究它的减阻机理。因先忽略网格尺寸的影响，根据经验选择适中的网格尺寸，对湍流模型和网格类型这两种影响因素进行探讨，选择4种湍流模型和4种网格类型，通过组合，共有16个Case。对这些Case进行初步的评价，找出效果较好的4个Case，选定这4种仿真方案，进一步去进行网格尺寸的研究。在这一阶段，会对网格类型、网格尺寸与湍流模型这3种影响因素进行最终评价，得到最优仿真结果。本部分仿真研究共涉及32个Case，选定最优仿真方案后，在35°Ahmed模型尾部斜面上端添加凸起结构，通过改变凸起与模型背部的夹角去研究被动控制技术对减阻的影响，并实现一定程度的减阻。

1 数值仿真方案的设定

由于空气相对于汽车的流速低于0.3个马赫数，在汽车外流场的仿真中，空气可以被看作是理想的气体[13]，具有不可压缩性，我们采用离散控制方程，应用有限体积法去求解。我们从控制方程的空间离散格式与松弛因子这两个方面去设置求解器。空间离散格式对计算的稳定性有较大影响，松弛因子对方程的求解速度有较大影响，这两个因素都影响着计算结果的精确性。本文采用满足二阶精度的离散格式。

汽车外流场仿真精确性研究的具体方案为：第一阶段，先忽略网格尺寸的影响，根据经验选择适中的网格尺寸，选择4种湍流模型和4种网格类型作为研究对象，组合出16个Case，如表1所示，对这些Case进行初步的评价，找出效果较好的4个Case；第二阶段，在第一阶段选定的4种方案的基础上，探讨网格尺寸对仿真精确度的影响，这一阶段也会有16个Case，如表2所示。最后，会得出这3种影响因素的最终评估结果，得出最优仿真方案。研究中为方便描述，将四面体网格用符号TE表示，六面体网格用符号T表示，多面体网格用符号P表示，十二面体网格用符号TD表示。将标准k-e湍流模型用符号KS表示，Realizablek-e模型用符号KR表示，SSTk-w模型用符号KW表示，Reynolds应力模型用符号TL表示。将最小加密体的网格尺寸用数字表示，4表示最大值，为20 mm，3表示网格尺寸为15 mm,2表示网格尺寸为10 mm，1表示网格尺寸为5 mm。鉴于湍流模型的选取受壁面函数的影响较大，本文根据经验将壁面函数的值设置在允许的范围内。

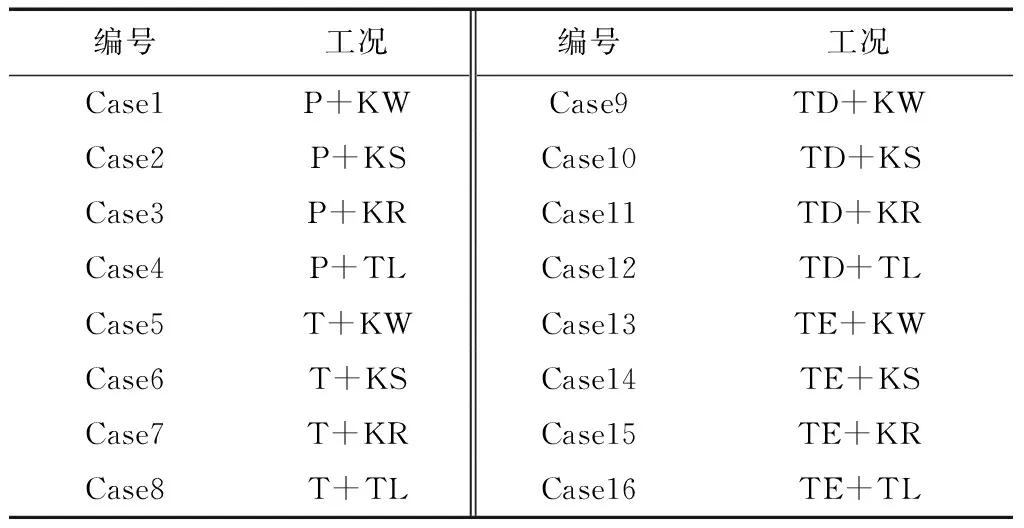
表1 第一阶段仿真方案设定

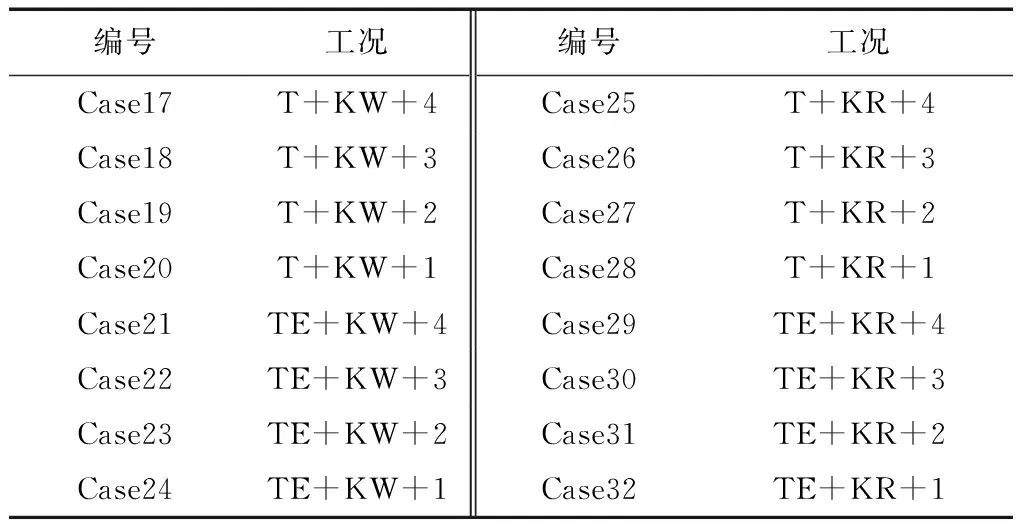
表2 第二阶段仿真方案设定

本仿真采用具有35°后窗倾角的Ahmed模型，总的风阻系数Cw由压差阻力系数Cp和摩擦阻力系数Cr组成，其中，压差阻力系数包含了前端的压差阻力系数Ck、尾部斜面的压差阻力系数Cs和尾部垂直面的压差阻力系数Cb。本文采用的数字风洞为15 m×3 m×1.5 m的长方体计算域，模型的阻塞比不超过1%，基本满足了要求的阻塞比。模型到入口的距离约为模型长度的4倍，模型到出口的距离约为模型长度的8倍。这样的设置使模型周围有足够大的空间，使它附近特别是尾部的空气流动能够充分发展。为保证与风洞试验的数据保持一致，将模型底部与地面的距离设置为50 mm[5]，设定60 m/s的来流速度，雷诺数Re为4.29×106，湍流[14]强度小于0.5%。采用分离式的求解器，适中的松弛因子和二阶精度的空间离散格式。

如图1模型设定两重加密体，为进行网格尺寸的研究[15]，把第一重加密体的网格尺寸设置成可变化的；采用5层棱柱层网格对边界层进行模拟。图2为边界层网格示意图，图3为模型表面的Y+云图，可见模型表面的Y+值基本控制在20～100之间，这保证了对边界层流动的仿真更准确[16]。

图1 几何模型与网格空间整体布置图

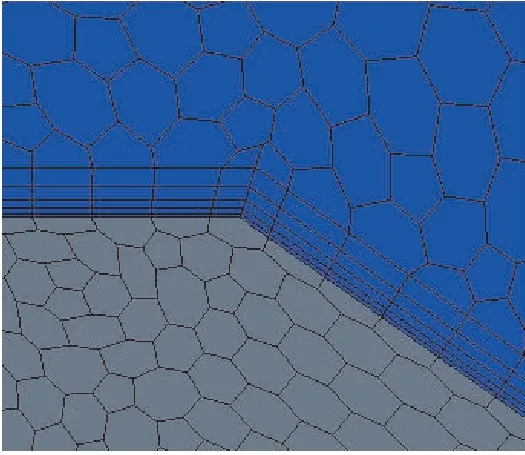
图2 边界层网格示意图

图3 模型表面Y+云图

计算模型的物理条件及求解参数设置如表3所示。

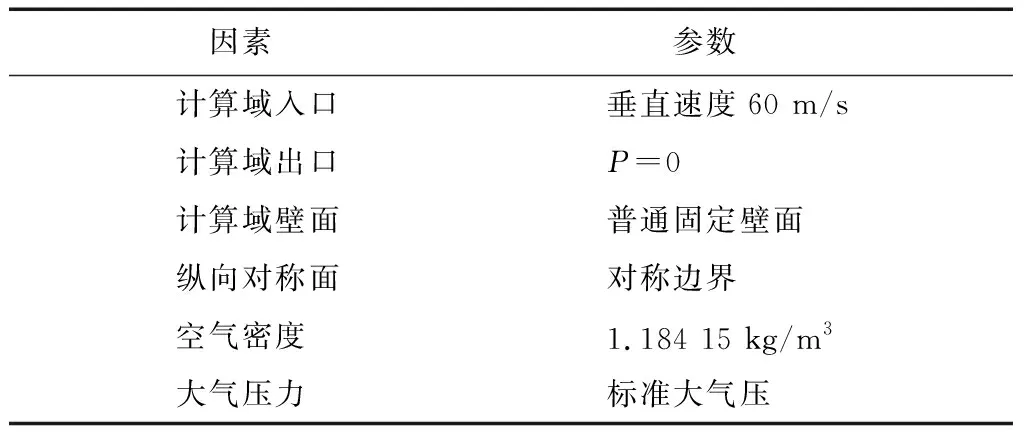
表3 仿真相关参数设置

2 仿真精确性研究

工程上的误差一般允许在5%左右，为得到更为精确的仿真策略，使仿真结果的误差不超过1%，本文依次从整体阻力系数、局部阻力系数、模型尾部流场的物理量具体数据这3个层级进行分析评价，使结论更有说服力。

2.1 第一步仿真分析

此阶段仿真采用适中的网格尺寸，这样可以节约时间，快速地获得计算结果，探讨湍流模型和网格类型对仿真精确度的影响。在这一步分析中，主要考虑整体风阻系数和局部风阻系数这两个评价指标，且以整体风阻系数为主。结果如表4所示。其中的试验值参考文章Ahmed et al.1984[5]；表4中Cp是总的压差阻力系数，仿真的结果均精确到小数点后第3位即千分位；由于T+TL和TE+TL两种情况下的计算结果是发散的，不予考虑。

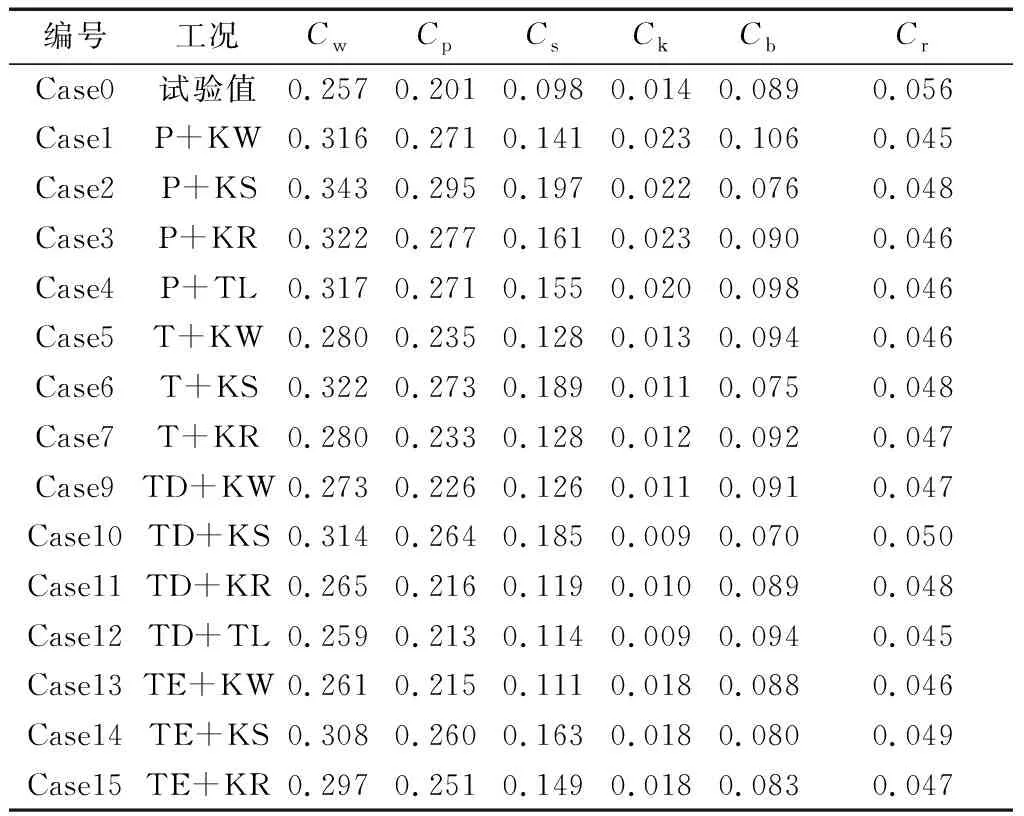
表4 初步仿真结果

从表4中的仿真结果可知，各个工况下Cr的值基本一样，即模型总摩擦阻力系数基本不变，因此，该模型的主要阻力为它的压差阻力。在此，忽略模型摩擦阻力系数对阻力的影响，主要研究它的压差阻力系数。

图4是总的压差阻力系数Cp的折线图，试验数据在图中用红色水平直线表示，4种网格和4种湍流模型的仿真数据如图所示。

图4 第一步仿真的总压差阻力系数

图5是在第一步仿真中，采用适中的同一尺寸的网格时，4种类型体网格模型所生成的网格数量对比图。对网格数量进行归一化处理，其中以1表示多面体网格P的数量，归一化处理后，其余类型网格的数量如图5所示。

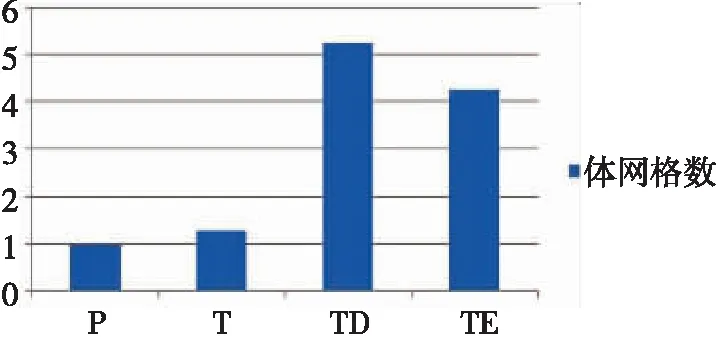
图5 第一步仿真体网格数量对比

经过分析研究，可以排除P和TD这两种网格，以及KS和TL这两种湍流模型。下面将对由SSTk-w、Realizablek-e这两种湍流与四面体网格、六面体网格这两种网格类型组合的工况做进一步的研究。

2.2 第二步仿真分析

在第一步仿真分析中，已经确定了几种有效的仿真方案，接下来还需对这些方案的网格进行精细处理。通常局部较复杂的流场对网格的精细度要求比较高[17-18]，网格过大不易捕捉到流场的细节信息，因此我们选择局部阻力系数作为第二级评价指标，从而对仿真的精确度做进一步的研究。

表5为第二步仿真的结果，表中的所有数据精确到千分位。从表5中，可以看出一个很明显的特征，即仿真中的摩擦阻力值和试验值也相差10个count左右，这与之前第一步仿真中得到的值一样都相对一致。因此，在这步的研究中，我们同样忽略摩擦阻力的影响，将压差阻力作为主要研究对象。

表5 第二步仿真结果

图6纵坐标Cp表示模型总的压差阻力系数的值，横坐标代表网格的大小。网格尺寸经过归一化处理后如图所示，红线表示模型在风洞中测得的试验值。从图6中可以明显地看出，总体上Cp值随着网格尺寸的减小而逐渐减小，从大于试验值降到等于试验值，再到小于试验值。对比分析可以看出，仿真计算的精确度与网格设置的大小有很大关系，网格大小的设置应该限制在一定量级，采用适中的网格尺寸。从图6可知，这些仿真工况中精确度最高的工况为Case28，即T+KR+1组合，其次为Case19和Case23,即T+KW+2和TE+KW+2这两个组合，下面将对这几个工况的局部阻力系数作深入的分析。

图6 第二步仿真总压差阻力系数

图7为选定3个工况与试验值对比的Cp值条形图。可以清晰地看到各个工况的总压差阻力系数与试验值之间的误差关系，由该图所得的结论与前面所作的分析结果是一致的。

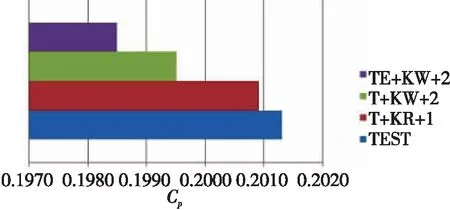
图7 3种组合Cp仿真值与试验值比较

图8为3种组合工况中Ahmed模型的前端、尾部斜面、尾部垂直面的局部风阻系数与试验值对比。从图8可以清晰地看出，在局部部位的风阻系数中，方案TE+KW+2总是与试验值最为接近。而前面从图6中得到的最优组合T+KR+1的误差之所以最小，由图8可知这是在Ck、Cb值的过小与Cs值的过大双重作用下形成的，这是一种假象，不是理想的结果。

因此，我们得到仿真精度最高的方案是TE+KW+2组合，这个方案才是最优结果。其次较好的方案为T+KW+2组合，再次为T+KR+1组合。

2.3 局部流场物理量具体数据分析

为了进一步验证第二步分析得到的3种组合的仿真精度，下面我们从局部流场的数据即分离涡剪切层附近的流速来进行分析。

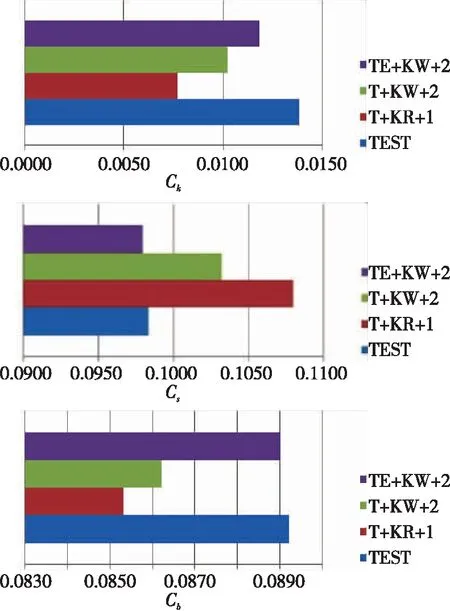
图8 局部压差阻力系数对比

如图9所示，在模型尾部斜面的对称面上选取4条竖直线，选定直线上特定位置的点，将仿真得到的这些点的速度值与已有的风洞试验值作对比，进一步验证前面所得的结果。

图9 数据选取的位置

图10为选定4条直线上各个方案仿真速度值与试验值的对比，从中我们可以明显地看到：

1)选定的3个工况与试验数据相比，均没有与试验值完全吻合，均存在一定的误差。

2) 在这3个工况中，工况TE+KW+2与试验值吻合最好，误差程度最小，可以确定为仿真精确度最好的方案，这与前面所得结论是一致的。

综上可知，本文所得的最优仿真方案为TE+KW+2这个工况，该方案应用四面体网格。由于四面体网格生成的网格数量要比六面体网格多，相应的计算量就会加大，在工程应用中，需要考虑计算时间、成本等因素，因此可以根据具体情况选择合理的方案进行仿真。

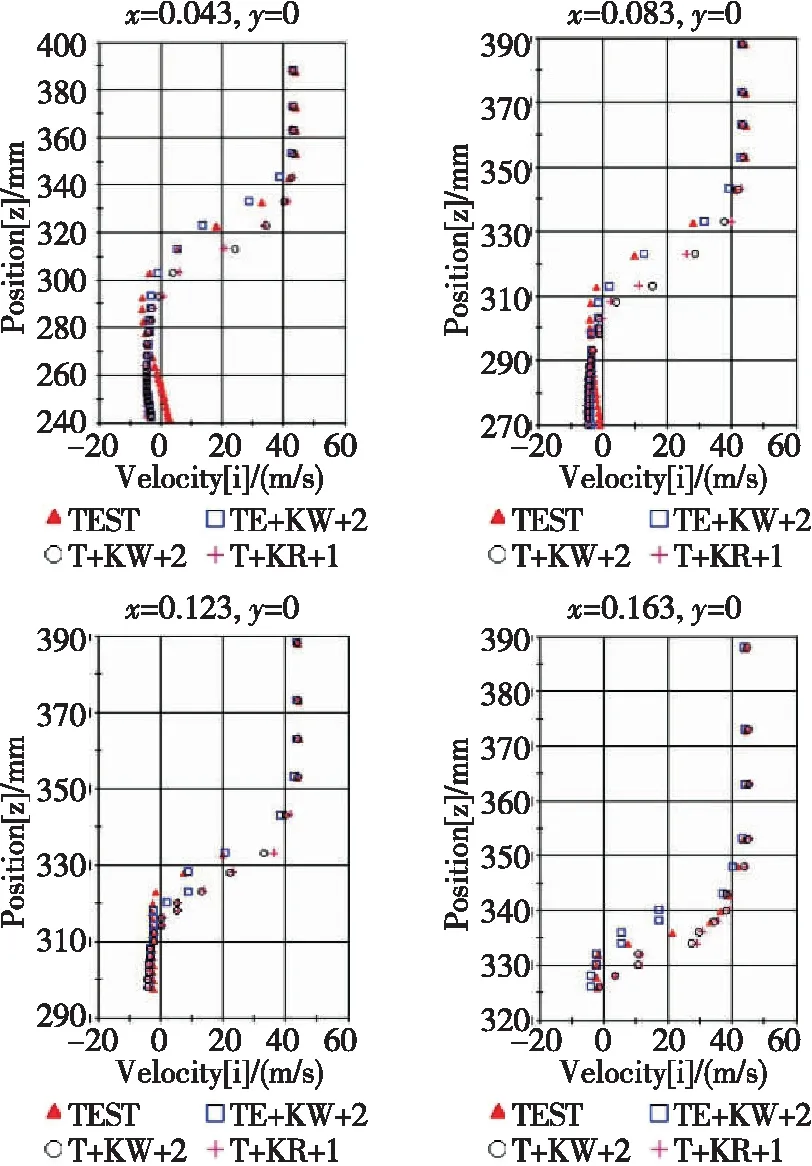
图10 剪切层处的气流纵向速度变化对比图

3 被动控制减阻研究

3.1 减阻方案设定

减阻方案如图11所示。

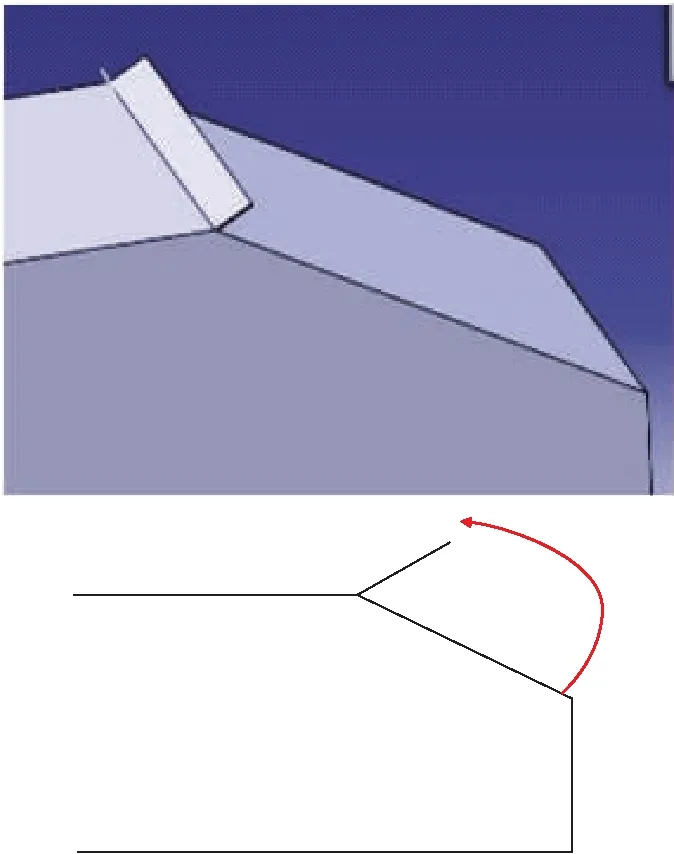
图11 减阻方案示意图

参考第2部分的研究结果，本文采用精确仿真的方法，在35°Ahmed模型尾部斜面上端添加厚度为1 mm，高度为20 mm的凸起结构，如图11所示，以凸起与尾部斜面的夹角为变量，从0°开始以10°为间隔递增，找到模型的最优减阻工况。

3.2 仿真结果

由于Ahmed模型的风阻主要来自于压差阻力，下面的研究将以Ahmed模型的压差阻力系数为评价指标进行研究。Ahmed模型被动减阻仿真结果如表6所示。

表6 被动减阻方案计算结果

从表6可以看出，随着夹角的增大，模型的压差阻力系数的变化趋势是先减小再增大，然后再减小。当附加板与斜面角度为30°时，模型的压差阻力系数最小，此时的值为0.190，相对于原始数模的压差阻力系数减小了11个count，有较好的减阻效果。

3.3 后处理分析

选出减阻效果最好的工况，即附加板与斜面角度为30°的工况作深入的分析，探索Ahmed模型的减阻机理。由之前的分析我们知道，Ahmed模型的阻力主要来源于模型的尾部，因此重点关注模型的尾部斜面和竖直面区域。表7为最优减阻方案与原始方案的局部压差阻力系数对比表。从中可以看出模型尾部斜面的压差阻力系数变化更明显。

表7 标准模型与最优减阻方案结果对比

图12为标准35°Ahmed模型与最优减阻工况的尾部斜面压力云图[17]。最优减阻工况斜面上的压力相较于标准模型有所增大，这就有效地减小了模型的压差阻力，而且C柱涡在斜面上的印记变的很弱。

图12 尾部斜面压力云图

图13为标准35°Ahmed模型与最优减阻工况的纵向对称面上的速度矢量图，优化模型的尾部分离涡相较于原始模型变化不明显。

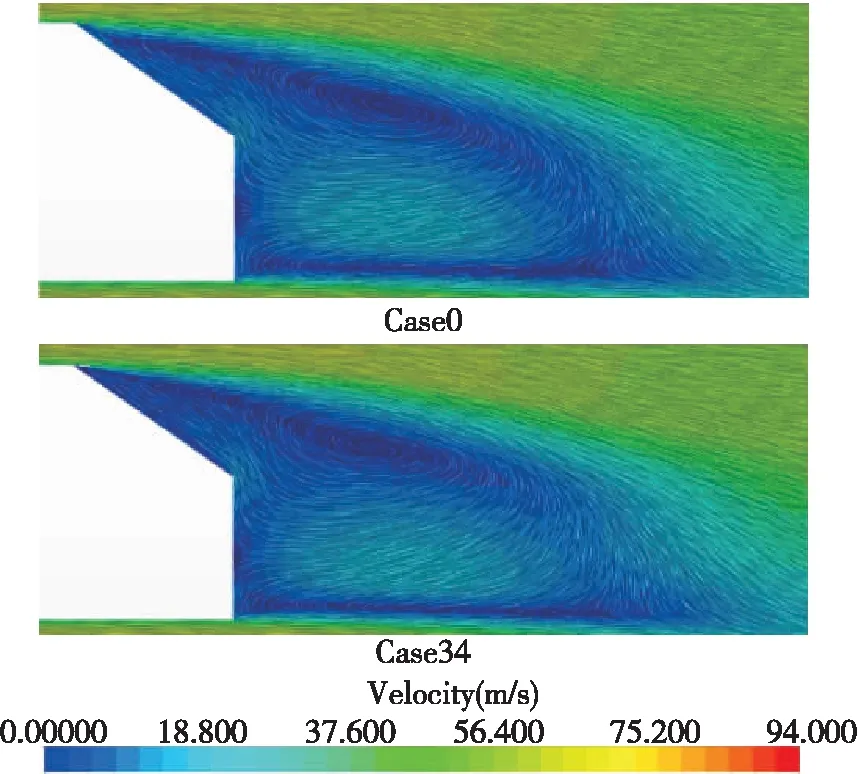
图13 纵向对称面上速度矢量图

图14为标准35°Ahmed模型与最优减阻工况的尾部10 mm处横截面上的速度云图。从中可以看出减阻方案尾部斜面上的分离区域有所扩展，与C柱涡融合得更强些，C柱涡的强度明显减弱。

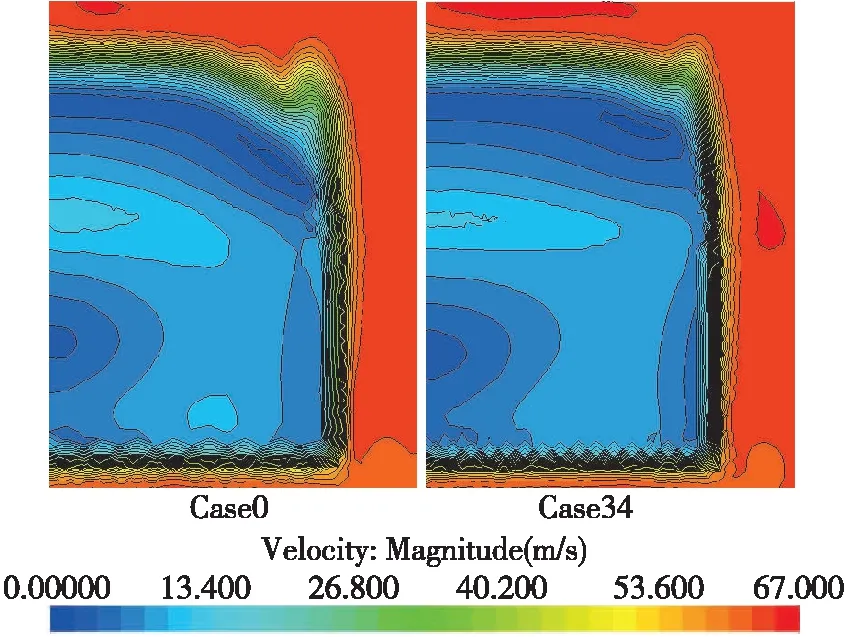
图14 尾部10mm处横截面上速度云图

4 结论

本文采用数值模拟的方法，从网格类型、湍流模型、网格尺寸这3个影响因素出发，分3个评价层次对汽车外流场的仿真精确性进行了研究，找到了精确度高的仿真策略，在保证仿真精确度的基础上，对Ahmed模型被动控制减阻技术作了研究，可以得到如下结论：

1)数值模拟的精确性受网格类型、湍流模型和网格尺寸等因素的影响比较大，在进行仿真计算前，有必要对仿真精确度进行研究，确保计算结果的可靠性。

2)对于35°Ahmed模型，它的阻力主要来源于模型尾部。本文研究了模型尾部添加凸起结构对减阻的影响，当附加板与斜面角度为30°时，有最优减阻效果。

3)凸起结构的作用主要是改善了35°Ahmed模型周围流场的分布，从而有效地减小了模型的压差阻力。