基于四种截集的粗糙模糊集表现定理的新表示
何天荣
(丽江师范高等专科学校 教师教育学院,云南 丽江 674199)
粗糙模糊集理论[1-7]是粗糙集理论[8-9]与模糊集理论[10-11]的整合研究,二者都是对经典集合理论的推广,都是用来研究知识的不确定性与不完全性的理论,但二者的侧重点不同,因此具有很强的优势互补性.分解定理与表现定理并列为模糊数学最基本的定理,它从另外的角度阐述了模糊集合由经典集合扩充而来.关于粗糙模糊集构造性质的研究,基于上截集形式的粗糙模糊集的分解定理、表现定理、扩展原理的研究成果居多[12-17],如袁学海等[18]提出了四种新的截集并研究了基于这四种截集有形式的模糊集的分解定理,蒋劲松等[19]研究了交与并的表示下粗糙模糊集的分解定理,何天荣[20]研究了并的表示下基于四种截集形式的粗糙模糊集的构造性质.目前,交的表示下基于四种截集形式的粗糙模糊集的表现定理和扩展定理的研究成果尚未出现.粗糙模糊集表现定理的新表示是在粗糙模糊集交的定义下基于四种截集的粗糙模糊集的表现定理,因为结论是基于交的表示及相应分解定理的前提下得出的,所以所得结论与基于并的粗糙模糊集的表现定理的结论形式完全不同.定理的证明需要借助基于交的粗糙模糊集的分解定理及粗糙模糊集的交的表示定义,四个定理的证明具有相似性,只要详细证明其中两个定理,其余两个定理的证明可以用与已证明的两个定理完全类似的方法证明.
1 粗糙模糊集及截集
为了系统研究基于四种截集的粗糙模糊集的表现定理,首先引入两个重要概念:粗糙模糊集及它的四种截集,将模糊数学中原有的截集称为λ-上截集,将与上截集隶属函数不等号方向相反的截集称为λ-下截集;再以补集形式分别定义λ-下重截集与λ-上重截集.分解定理及表现定理的理论证明基于各种截集的定义及粗糙模糊集交的定义.
1.1 粗糙模糊集

(1)
(2)
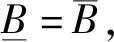
1.2 粗糙模糊集的四种截集
定义2[18]设B是论域V上的一个模糊集,λ∈[0,1],称:
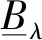
同理可以定义以下3种截集.

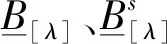
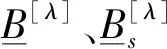
2 交的表示形式的粗糙模糊集及分解定理
2.1 交的表示形式的粗糙模糊集
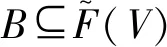

(3)
把这样的定义称为粗糙模糊集的交的表示,是相对于粗糙模糊集的并的表示:

(4)
而言的,接下来的分解定理及表现定理的结论都是基于交的表示形式下得到的.
2.2 基于交的四种截集形式的粗糙模糊集分解定理
根据模糊子集的交的表示方式,可以得到以下4个分别基于四种截集形式的粗糙模糊集的分解定理,定理结论引自文献[19],这里直接给出结论,不作证明,证明的过程可以参考相关文献.
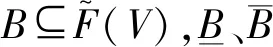
定理1[19](基于上截集形式的粗糙模糊集的分解定理):

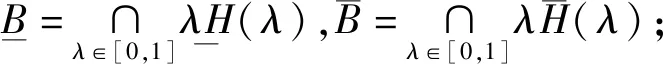
定理2[19](基于下截集形式的粗糙模糊集的分解定理):
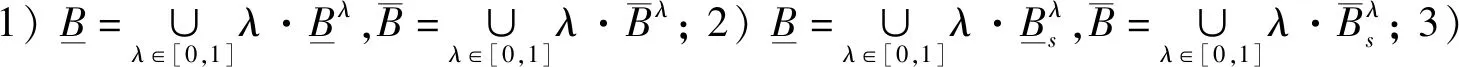
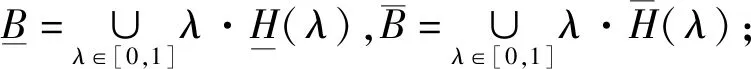
定理3[19](基于下重截集形式的粗糙模糊集的分解定理):

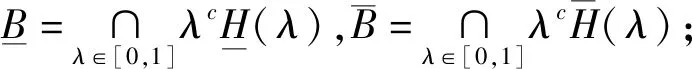
定理4[19](基于上重截集形式的粗糙模糊集的分解定理):

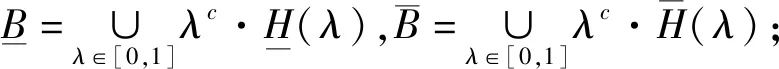
3 四种截集形式粗糙模糊集的表现定理
表现定理是粗糙模糊集的基本定理,是粗糙模糊集构造性质的重要组成部分,它从另一个角度阐明粗糙模糊集是由粗糙集扩充而成的,描述的是每个集合套都可以表示成一个粗糙模糊子集.接下来首先引入集合套的定义及性质,再给出四个表现定理并证明其中具有代表性的两个定理.
3.1 集合套及其基本性质
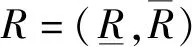


3.2 基于四种截集形式的粗糙模糊集的表现定理
基于粗糙模糊集交的表示定义及对应于四种截集的4个分解定理可以得到以下4个表现定理,为节省篇幅,仅证明定理6和定理7,定理5的证明类似于定理7,定理8的证明类似于定理6.

上截集是模糊集最原始的截集概念,基于并的上截集形式的粗糙模糊集的表现定理的研究成果相对较多,本定理是基于交的上截集形式的粗糙模糊集的表现定理,可以理解为前者的并行研究,定理结论的证明可以用完全类似于定理7的方法,而定理7是基于下重截集的粗糙模糊集的表现定理,下重截集是引入的新的截集定义[18],为节省篇幅,选择详细证明更具有代表性的定理7,而定理5的证明不再赘述.
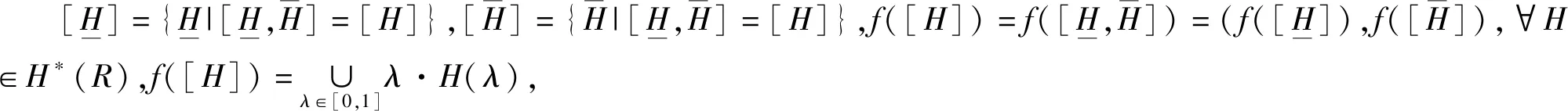
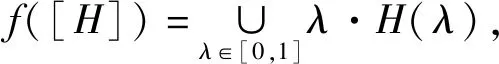
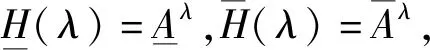


即定理6的结论2)和结论3)成立.

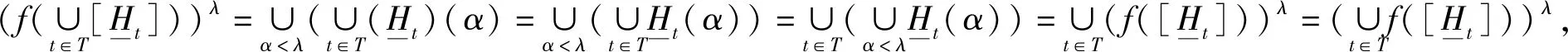
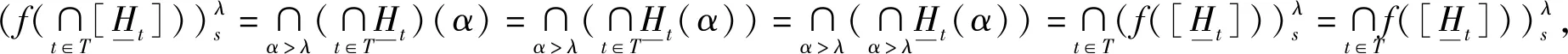
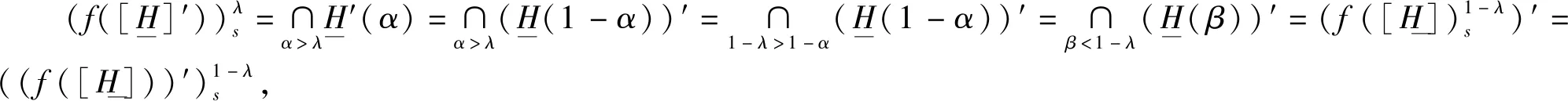
所以f是(H*(R),∪,∩,’)到(A*,∪,∩,’)的满同态映射.
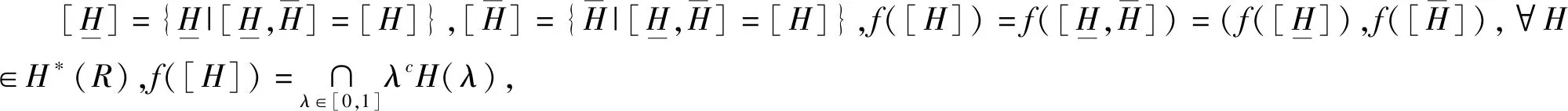
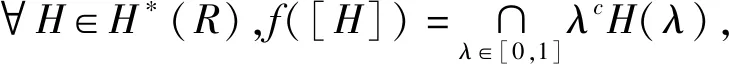
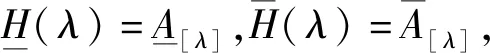
其次证明定理7的结论1)、2)、3)成立.
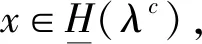

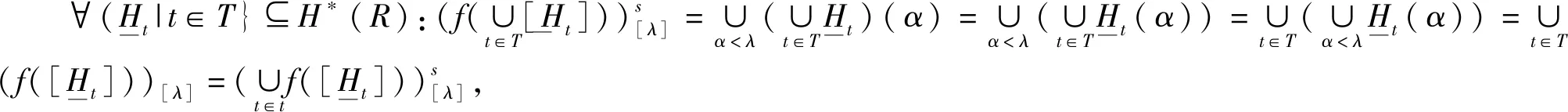


所以f是(H*(R),∪,∩,’)到(A*,∪,∩,’)的满同态映射.

本定理的证明完全类似于定理6,在此不做赘述.
4 结语
引入粗糙模糊集的四种截集,并在粗糙模糊集交(定义3的(3))的表示形式下系统研究了粗糙模糊集基于四种截集形式的四个表现定理,并系统证明了其中具有代表性的两个定理,其余两个定理的证明完全类似于已证明的两个定理.本文得出的四个表现定理结论完全不同于基于并(式4))的粗糙模糊集的表现定理[20],其本质原因在于文献[20]所得结论是基于粗糙模糊集的并的表示及基于并的四种截集形式是分解定理;而本文所得结论的理论依据是粗糙模糊集交的表示及基于交的四个分解定理.

