模的投射覆盖、内射包络与局部环①
(陇南师范高等专科学校数信学院,甘肃 陇南 742500)
0 引 言
局部环是环模理论中重要的环类之一.其应用非常广泛.设R是有单位元的结合环.若对任意r∈R,有r可逆或者1-r可逆,则称环R为局部环[1].若模M的自同态环End(RM)是局部环,则模M是不可分解模[2].设g:X→C为模同态.若对任意满足等式gα=g的同态α:X→X,都有α为同构,则称g:X→C是右极小的[3].对偶地可定义左极小同态.设x为左R-模范畴的一个子范畴且X∈x.若对任意X′∈x及同态f:X′→C,都存在同态β:X′→X使得gβ=f,则称g:X→C为模C的x-预覆盖[4].若g:X→C是C的右极小x-预覆盖,则称g:X→C为模C的x-覆盖.对偶地,可定义x-预包络和x-包络.若模Q既是投射模又是内射模,则简称Q为投射-内射模.本文主要研究左R-模的投射盖、内射包络与局部环之间的关系,并进一步完善环模理论与同调代数中与其相关的基础理论.
1 本文引理
引理1[1]设M,M′,N,N′都是左R-模,f:M→N为左R-模同态.
(1)如果g:M→M′是满同态且Kerg⊆Kerf,那么存在唯一确定的同态h:M′→N,使得f=hg.
(2)如果g:N′→N是单同态且Imf⊆Img,那么存在唯一确定的同态h:M→N′,使得f=gh.
引理2[5]设下图为左R-模行正合交换图,
则存在唯一的同态f∈HomR(A,A′),使得gi=i′f.
引理3[5]设下图为左R-模行正合交换图,

(2)当t2,t4为单同态且t5为满同态时,t3为单同态.
(3)当t1,t2,t4,t5为同构时,t3为同构.
引理4[2]设M是一个具有有限长度的不可分解模,那么End(M)是局部环.
2 主要结果
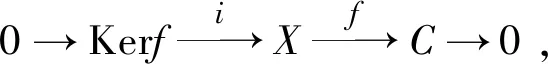
由假设知,自同态环End(Kerf)是局部环.从而β为同构或者1Kerf-β为同构.
若β为同构,则由引理5易得α为同构.
若1Kerf-β为同构,则i(1Kerf-β)=i-iβ=i-αi=(1X-α)i.因为f(1X-α)=f-fα=f-f=0,所以Im(1X-α)⊆Kerf=Imi.根据引理1知,存在同态γ:X→Kerf,使得iγ=1X-α.因为iγi=(1X-α)i=i(1Kerf-β),i为单同态且单同态左可消,所以γi=1Kerf-β.
可见γi为同构.从而存在同态γ′∈End(Kerf),使得γ′(γi)=1Kerf.显然γ′γ是X到Kerf的同态.所以单同态i可裂.从而满同态f也可裂.这与假设矛盾.因此1Kerf-β不是同构.
定理2 设g:A→X为非可裂的单同态且End(Cokerg)为局部环,则g是左极小的.
由假设知,自同态环End(Cokerg)是局部环.从而α为同构或者1Cokerg-α为同构.
若α为同构,则由引理3易得β为同构.
若1Cokerg-α为同构,则有(1Cokerg-α)π=π-απ=π-πβ=π(1X-β).因为(1X-β)g=g-βg=g-g=0,所以Kerπ=Img⊆Ker(1X-β).由引理1知存在同态ρ:Cokerg→X,使得ρπ=1X-β.又因为(πρ)π=π(ρπ)=π(1X-β)=(1Cokerg-α)π,π为满同态且满同态右可消,所以πρ=1Cokerg-α为同构.可见存在同态ρ′,使得(πρ)ρ′=1Cokerg,即π(ρρ′)=1Cokerg.易知π:X→Cokerg为可裂满同态.从而单同态g:A→X也可裂.这与假设矛盾.因此1Cokerg-α不是同构.

(1)若End(A)为局部环,则同态f为右极小的.
(2)若End(C)为局部环,则同态g为左极小的.
证明由定理1和定理2易证.
定理3 设f:Q→X为非投射模X的投射覆盖,Q是投射-内射模且End(X)为局部环,则包含同态i:Kerf→Q为Kerf的内射包络.
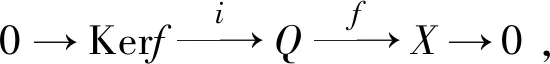
因此包含同态i:Kerf→Q为Kerf的内射包络.
推论2 设X是具有有限长度的不可分解模,f:Q→X是非投射模X的投射覆盖且Q是投射-内射模,则包含同态i:Kerf→Q为Kerf的内射包络.
证明因为X是具有有限长度的不可分解模,由引理4知自同态环End(X)为局部环.根据定理3可得,包含同态i:Kerf→Q为Kerf的内射包络.
有了上面的结论,对偶地可得如下定理和推论.
定理4 设g:Y→E为非内射模Y的内射包络,E是投射-内射模且End(Y)为局部环,则标准投射π:E→Cokerg为Cokerg的投射覆盖.
推论3 设Y是具有有限长度的不可分解模,g:Y→E是非内射模Y的内射包络且E是投射-内射模,则标准投射π:E→Cokerg为Cokerg的投射覆盖.

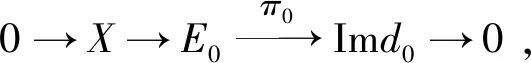
由引理3知h为同构.可见X≅X1⊕X2.由已知条件End(X)是局部环可得,X为不可分解模.从而X1=0或X2=0.若X1=0则有正合列0→X→Q2→N2→0且Q2≅N2≠0.而E0≅Q1⊕Q2,这与已知“X→E0是X的内射包络”矛盾.类似地,若X2=0,则同样会出现矛盾.因此Imd0是不可分解模.
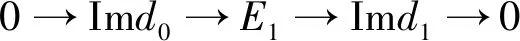

证明过程与定理5的对偶.
3 结 语
利用环模理论和同调代数的方法,研究了模的的投射覆盖、内射包络与局部环之间的关系.证明了如果同态f:Q→X是非投射模RX的投射覆盖且自同态环End(RX)为局部环,那么包含同态i:Kerf→Q为Kerf的内射包络;如果同态f:Y→Q是非内射模RY的内射包络且自同态环End(RY)为局部环,那么标准投射π:Q→Cokerf为Cokerf的投射覆盖.结果表明,模的的投射覆盖、内射包络与局部环之间有着密切的联系.从而补充了与其相关的结论,进一步完善了对模的投射覆盖、内射包络,以及局部环等后续问题的研究,具有一定的理论价值.

