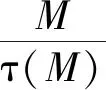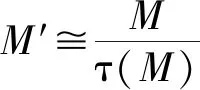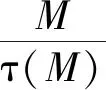对偶τ-Rickart模

李煜彦,何东林

(陇南师范高等专科学校 数信学院,甘肃 陇南 742500)

1 预备知识

定义1[14]称M是τ-Rickart模,如果对任意ψ∈End(M),τM(ψ)是M的直和因子.

定义2[6]称M是对偶Rickart模,如果对任意ψ∈End(M),Imψ=ψ(M)是M的直和因子.

引理1[13]τ-Rickart模的直和因子是τ-Rickart模.

引理2[13-14]设M是模,则下列条件等价:

1)M是τ-Rickart模;

2)M=τ(M)⊕M′,其中M′是(τ-挠自由)Rickart模;

3) 对任意f∈End(M),f-1(τ(M))是M的直和因子;

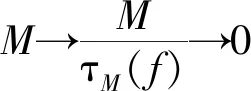
引理3[4]设M是模,S=End(M).则下列条件等价:

1)M是具有C2条件的Rickart模;

2)S是von Neumann正则环;

3) 对任意φ∈S,Kerφ和Imφ是M的直和因子.

2 主要结论

命题1设M是模，则以下结论成立:

1) 若M是τ-挠自由模,则M是对偶τ-Rickart模当且仅当M是对偶Rickart模;

2) 若M是非奇异模,则M是对偶t-Rickart模当且仅当M是对偶Rickart模;

3) 若M是τ-挠自由且非奇异模,则M是对偶τ-Rickart模当且仅当M是对偶t-Rickart模当且仅当M是对偶Rickart模.

证明显然.

由文献[13-15]知,直和因子包含τ(M)的τ-Rickart模和τ-Baer模分别具有SIP性质和强SIP性质.对偶地,直和因子包含τ(M)的对偶τ-Rickart模,下面结论成立.

命题2设M是模,N1,N2是M的且包含τ(M)直和因子.若M是对偶τ-Rickart模,则N1+N2是M的直和因子.

N1+N2=e1M⊕(1-e1)e2M=e1M⊕fM=

(e1+f-e1f)M

从而N1+N2是M的直和因子.

下面结论说明对偶τ-Rickart模保持直和因子.

定理1设M是模,L是M的直和因子.若M是对偶τ-Rickart模,则L是对偶τ-Rickart模.

证明设M=L⊕L′,ψ∈End(L).令φ=ψ⊕1L′,其中1L′是L′上的恒等自同态,则φ∈End(M).因为τ(M)=τ(L)⊕τ(L′),所以Imφ+τ(M)=(Imφ+L′)+(τ(L)⊕τ(L′))=(Imφ+τ(L))⊕L′.由于M是对偶τ-Rickart模,故存在N≤M,使得M=(Imφ+τ(L))⊕L′⊕N.于是L=(Imφ+τ(L))⊕[(L′⊕N)∩L)],即Imφ+τ(L)是L的直和因子.从而L是对偶τ-Rickart模.

由定理1,易得如下两个推论.

推论1R是对偶τ-Rickart环当且仅当每个循环投射R-模是对偶τ-Rickart模.

证明充分性) 显然.

必要性) 设R是对偶τ-Rickart环,M是循环投射R-模.则存在R的理想J,使得J是R的直和因子,且M≅J.由定理1知,J是对偶τ-Rickart模,因此M是对偶τ-Rickart模.

推论2设R是环,考虑以下条件:

1) 每个自由R-模是对偶τ-Rickart模;

2) 每个投射R-模是对偶τ-Rickart模;

3) 每个平坦R-模是对偶τ-Rickart模.

则3)⟹2)⟺1).当任意R-模是有限表示模时,2)⟹3).

证明因为自由模都是投射的,且投射模都是平坦的,所以3)⟹2)⟹1)成立.

1)⟹2) 设M是投射模,则存在自由模F,使得M是F的直和因子.由1)知,F是对偶τ-Rickart模,故由定理1知,M是对偶τ-Rickart模.

2)⟹3) 因为有限表示平坦模是投射的,故结论成立.

下面给出对偶τ-Rickart模的等价刻画.

定理2设M是模,则下列条件等价:

1)M是对偶τ-Rickart模;

2) 存在W≤M,使得M=τ(M)⊕W,其中W是(τ-挠自由)对偶Rickart模;

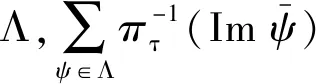
5) 对任意ψ∈End(M),短正合序列

是可裂的,其中ι和π分别是包含同态和自然满同态.

证明1)⟹2) 设M是对偶τ-Rickart模,0是M上的零同态.则τ(M)=Im 0+τ(M)是M的直和因子.于是存在W≤M,使得M=τ(M)⊕W,易知W是τ-挠自由的,由命题1和定理1知,W是对偶Rickart模.

2)⟹1) 设ψ∈End(M),ι:W→M是包含同态,π:M→W是标准投射.则

Imψ+τ(M)=Im(πψι)+τ(M)

因为W是对偶Rickart模,所以Im(πψι)是W的直和因子.因此Imψ+τ(M)是M的直和因子,从而M是对偶τ-Rickart模.

1)⟹3) 由命题2得证.

3)⟹4) 设I是End(M)的有限生成右理想,则存在ψi∈End(M)(i=1,2,…,n),使得

于是

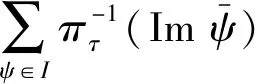
4)⟹1) 设φ∈End(M),I=φEnd(M).则

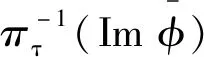
1)⟺5) 对任意ψ∈End(M),短正合序列

推论3若环R是半单的,则任意R-模M都是对偶τ-Rickart模,且其τ-挠子模τ(M)是投射的.

证明设ψ∈End(M).因为R是半单的,所以τ(M)是投射的,且短正合序列

可裂.由定理2知,M是对偶τ-Rickart模.

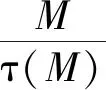
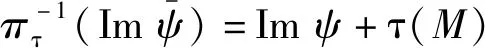
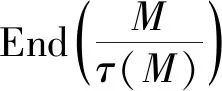
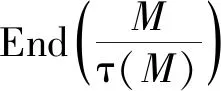
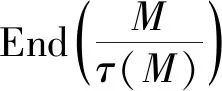
引理4[4]M是Rickart模当且仅当M具有D2条件并且对任意φ∈End(M),Imφ同构于M的某个直和因子.

引理5[6]M是对偶Rickart模当且仅当M具有C2条件并且对任意φ∈End(M),Imφ同构于M的某个直和因子.

由模的C2条件和D2条件可知,τ-Rickart模和对偶τ-Rickart模之间有如下联系.