李超代数Alg(K3,ω3)上的超双导子及超交换映射
黄忠铣
(1.武夷学院 数学与计算机学院,福建 武夷山 354300;2.福建省茶产业大数据应用与智能化重点实验室,福建 武夷山 354300)
设L是结合代数,如果映射ψ:L→L满足ψ(x)x=xψ(x),∀x∈L,则称ψ是交换映射.结合代数上的交换映射理论应用于李代数[1-3]、李超代数[4-7]等许多领域,产生了许多有趣的课题.若李超代数L上的映射ψ:L→L满足[ψ(x),x]=0,∀x∈L,则称映射ψ为李超代数L上的交换映射.李超代数上的交换映射分成标准和非标准的[4-5].Xia等[4]证明了超Virasoro代数上的所有线性超交换映射是标准的.Cheng等[6]证明了超伽利略共形代数上存在非标准的线性超交换映射.
超双导子是讨论结合超代数及李超代数上交换映射的有效途径[4-7].超双导子有内导子[4]和非内导子[6].对于李超代数L中的齐次元x,y,注意到有|φ(x,y)|=|x|+|y|.
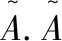
本文证明李超代数Alg(K3,ω3)上的超斜对称超双导子是内导子.并且证明此代数上的线性超交换映射是标准的.
在本文中,Z表示整数集,C表示复数域,所有的模(向量空间)都定义在C上.
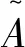
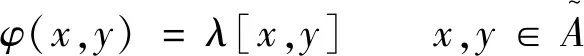
其中λ∈C.即Alg(K3,ω3)上的超斜对称双导子都是内导子.
证明由以下8部分证明完成.
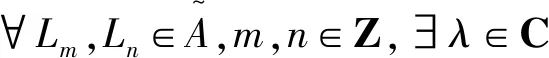
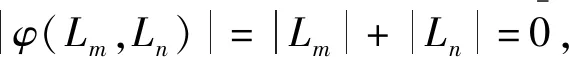
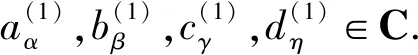
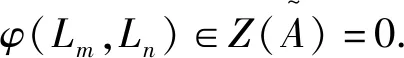
下面设m≠n,根据文[4]中推论2.2得
从而
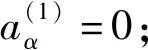
依据文[4]中引理2.1,有
[φ(Lm,Ln),[Lk,L0]]=[[Lm,Ln],φ(Lk,L0)]
k∈Z
可得
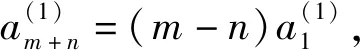
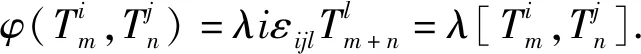
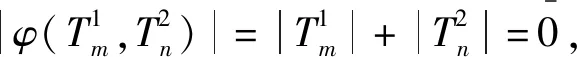
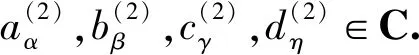
可得
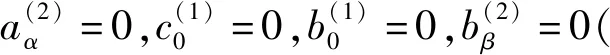

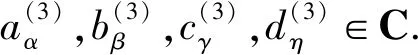
可得
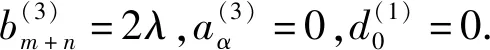
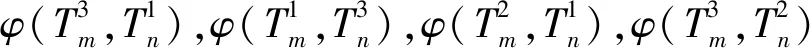
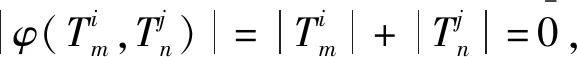
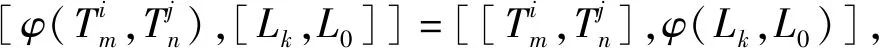
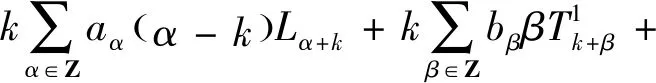
所以有如下形式:
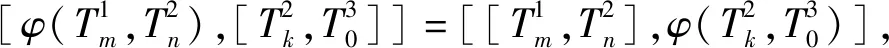
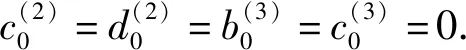
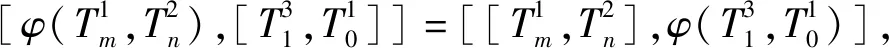
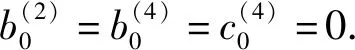
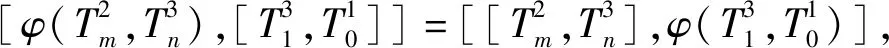
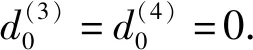
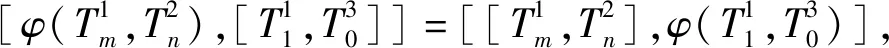
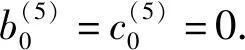
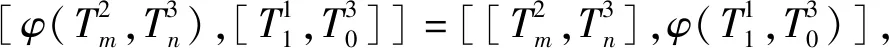
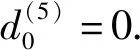
类似地,由
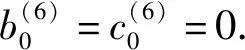
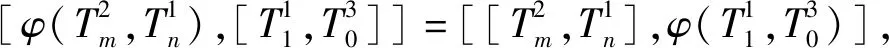
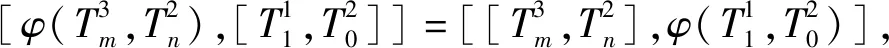
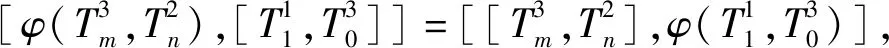
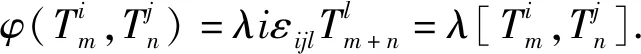
3) 欲证
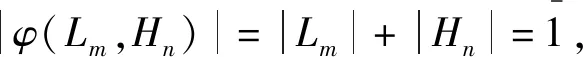
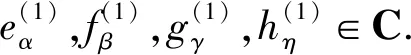
[φ(Lm,Hn),[L1,L0]]=[[Lm,Hn],φ(L1,L0)]
得
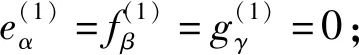
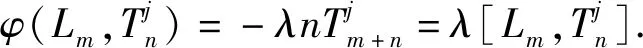
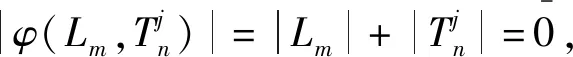
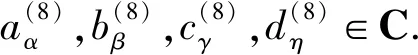
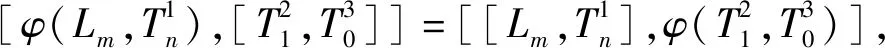
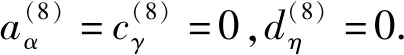
得
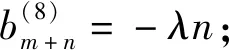
类似地,由
得
由
得
综上
5) 欲证
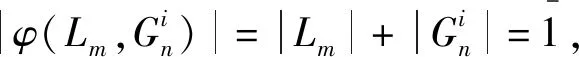
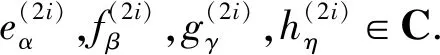
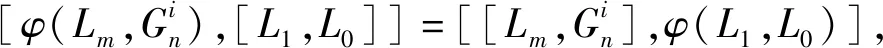
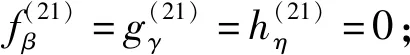
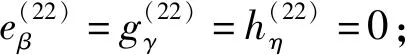
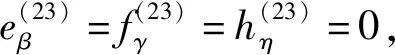
i=1,2,3
6) 欲证
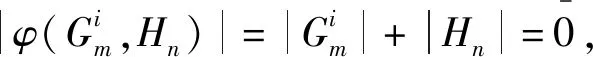
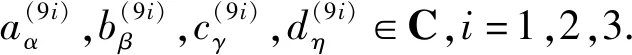
得
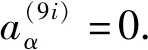
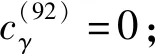
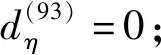
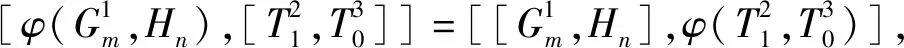
同理,利用
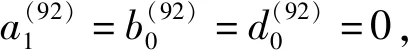
利用
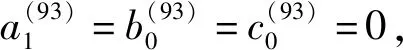
因此
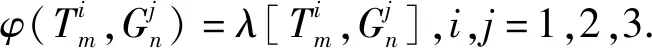
首先考虑若i≠j,且i,j=1,2,3的情形.因为
所以可设
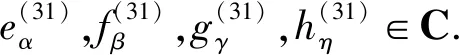
得
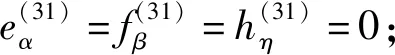
类似地,由
得
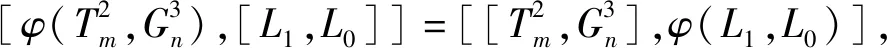
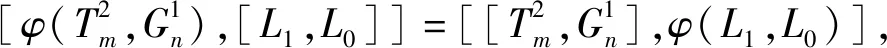
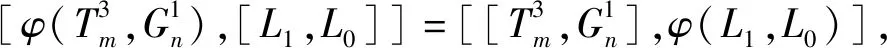
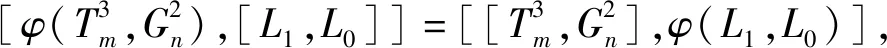
因此当i≠j时,
i,j=1,2,3
下面考虑若i=j,且i=1,2,3的情形.因为
所以可设
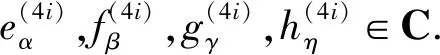
得
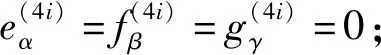
i=1,2,3
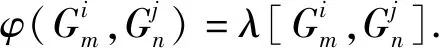
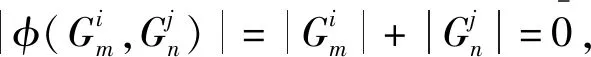
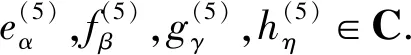
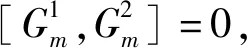
下面设m≠n,由
从而
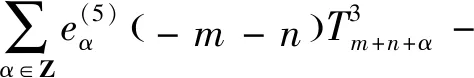
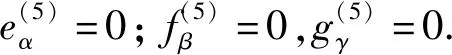
得
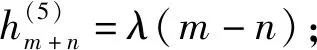
类似地,由
得
由
得
由
得
由
得
由
得
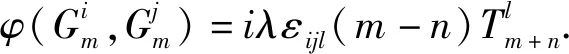
再考虑当i=j的情形.设
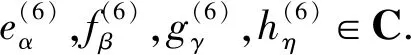
下面设m≠n,由
从而
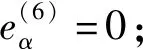
利用
得
所以
又由
得
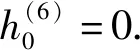
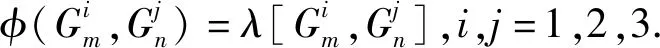
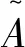
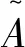
φ:G×G→G,φ(x,y)→[ψ(x),y]x,y∈G
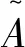
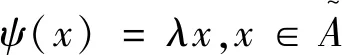
(1)
进一步地,在式(1)中取x=Gr,由[ψ(Gr),Gr]=0,可得λ=0.从而命题得证.

