剖分图的联图的距离矩阵相关谱
卢鹏丽,栾 睿,刘文智
(兰州理工大学 计算机与通信学院,甘肃 兰州 730050)
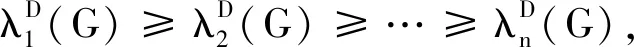


1 预备知识
图G的剖分图S(G)是在图G的每条边上添加一个新的顶点得到的.
定义1[12]设两个图G1和G2,将S(G1)中新添加的顶点与S(G2)中新添加顶点全部相连接,构造的图称为剖分边边联图,记为G1⊕G2.
定义2[13]设两个图G1和G2,将S(G1)中原有顶点与S(G2)中原有顶点全部相连接,构造的图称为剖分点点联图,记为G1◇G2.
定义3[13]设两个图G1和G2,将S(G1)中原有顶点与S(G2)中新添加顶点全部相连接,构造的图称为剖分点边联图,记为G1⊙G2.
引理1[14]设G是一个r-正则图,其邻接矩阵为A(G),关联矩阵为R(G),图G的线图记为L(G),I是与图G同维数的单位矩阵,则
R(G)R(G)T=A(G)+rI
R(G)TR(G)=A(L(G))+2I
设J为全一矩阵,则
JR(G)=2J=R(G)TJ
JR(G)T=rJ=R(G)J.
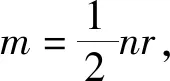
spec(L(G))=
且Z是特征值-2所对应的特征向量当且仅当RZ=0,其中R是图G的关联矩阵.
2 剖分边边联图的距离谱和距离(无符号)拉普拉斯谱
定理1设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分边边联图G1⊕G2的距离谱为
4) 矩阵的四个特征值
证明由剖分边边联图的定义可知其距离矩阵D(G1⊕G2)可表示为
其中:Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.
设Xij,i=1,2,j=2,3,…,ni为矩阵A(Gi)的特征值λij≠ri所对应的特征向量,即A(Gi)Xij=λijXij.则Xij和全一向量J正交,由引理1可知:
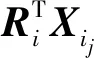
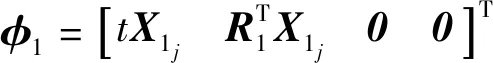
求解上述方程组可得
j=2,3,…,n1

求解上述方程组可得
j=2,3,…,n2
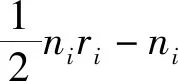
证毕
定理2设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分边边联图G1⊕G2的距离拉普拉斯谱为
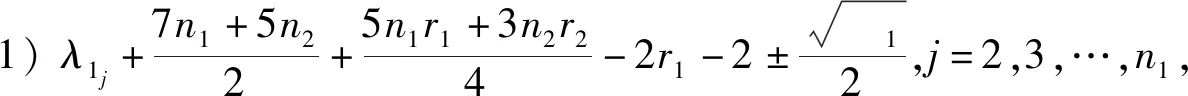
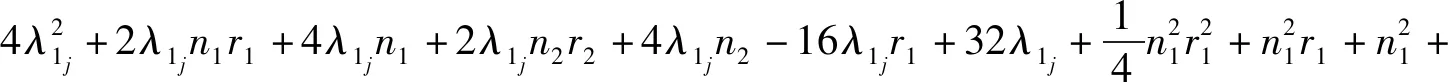
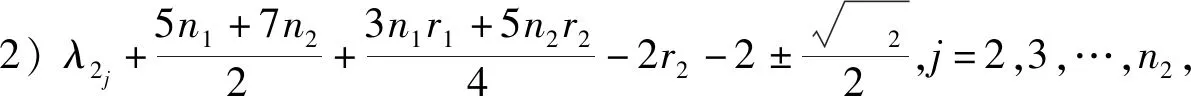
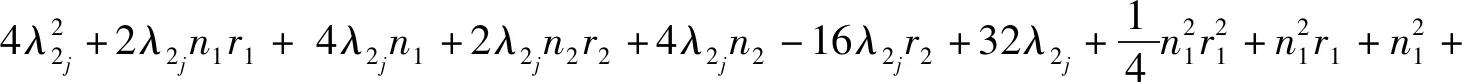
16r2+16
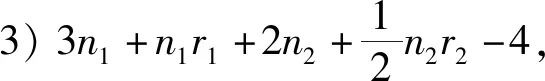
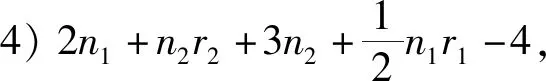
5) 矩阵的四个特征值
证明由剖分边边联图的定义可知其距离拉普拉斯矩阵DL(G1⊕G2)可表示为
其中

4J+2A(G2)
Ri是图Gi,i=1,2的关联矩阵,J为全一矩阵,I为单位矩阵.证明方法同定理1.
定理3设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分边边联图G1⊕G2的距离无符号拉普拉斯谱为
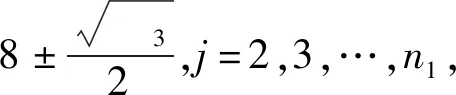
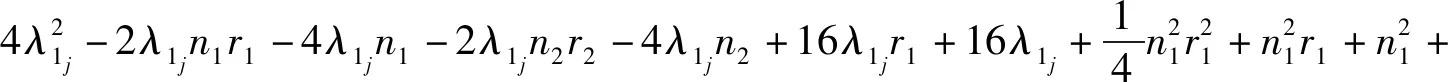
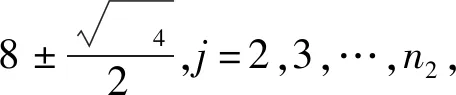
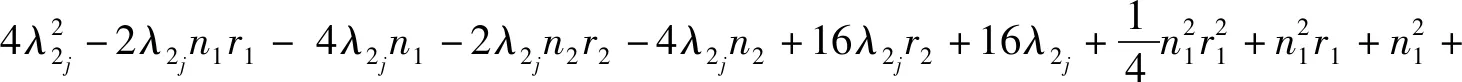
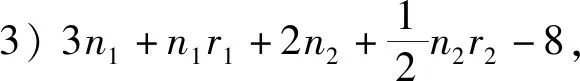
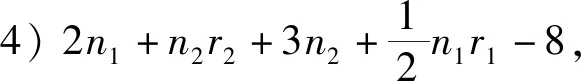
5) 矩阵的四个特征值
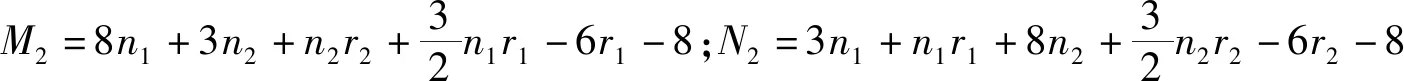
证明由剖分边边联图的定义可知其距离无符号拉普拉斯矩阵DQ(G1⊕G2)可表示为
其中
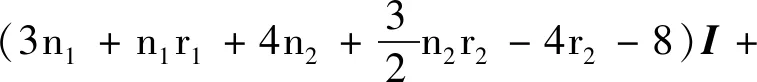
4J-2A(G2)
Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
3 剖分点点联图的距离谱和距离(无符号)拉普拉斯谱
定理4设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点点联图G1◇G2的距离谱为
1) -2(λ1j+r1+1),j=2,3,…,n1;
2) -2(λ2j+r2+1),j=2,3,…,n2;
4) 矩阵的四个特征值
证明由剖分点点联图的定义可知其距离矩阵D(G1◇G2)可表示为
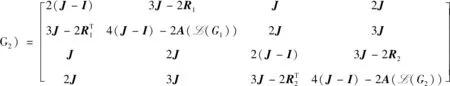
其中:Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
定理5设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点点联图G1◇G2的距离拉普拉斯谱为
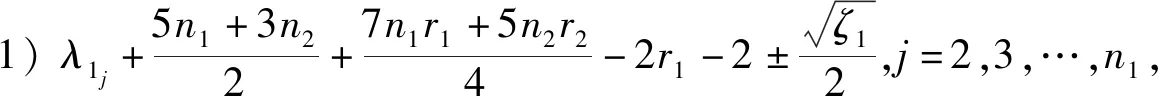

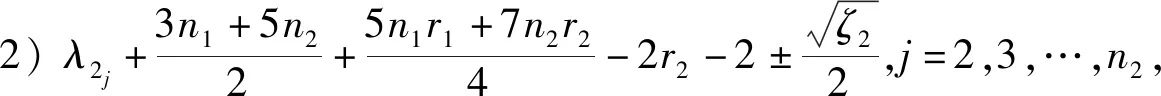
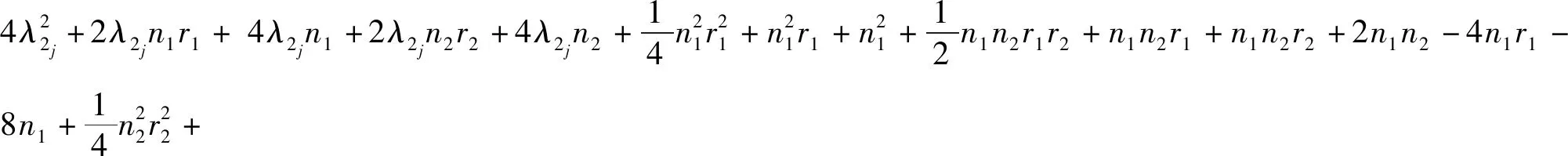
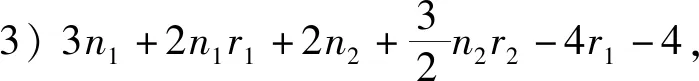
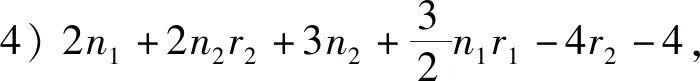
5) 矩阵的四个特征值
证明由剖分点点联图的定义可知其距离拉普拉斯矩阵DL(G1◇G2)可表示为
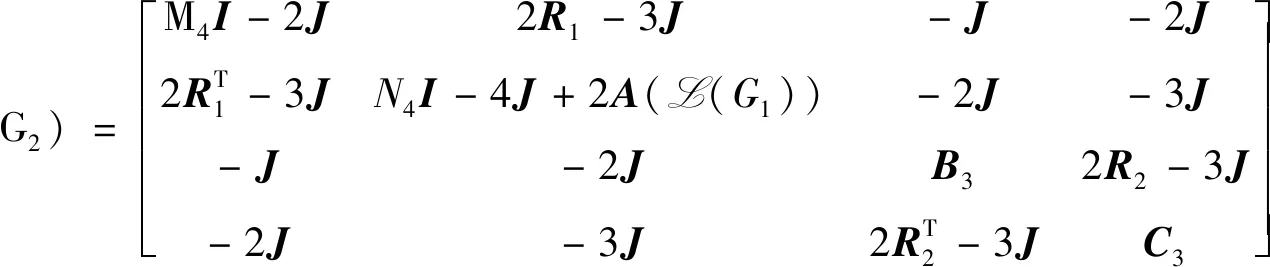
其中



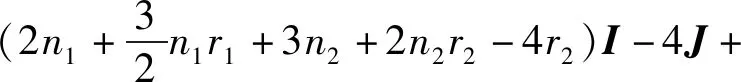
2A(L(G2))
Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
定理6设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点点联图G1◇G2的距离无符号拉普拉斯谱为


4λ1jn2+16λ1jr1+16λ1j+
n1n2r1+n1n2r2+2n1n2-

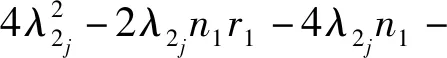
2λ2jn2r2-4λ2jn2+16λ2jr2+16λ2j+
n1n2r1+n1n2r2+2n1n2-
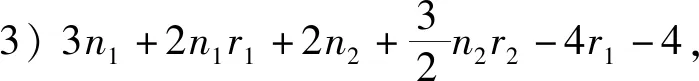
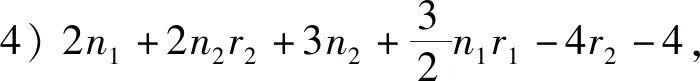
5) 矩阵的四个特征值

证明由剖分点点联图的定义可知其距离无符号拉普拉斯矩阵DQ(G1◇G2)可表示为
其中

4J-2A(L(G1)
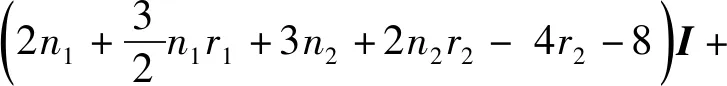
4J-2A(L(G2))
Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
4 剖分点边联图的距离谱和距离(无符号)拉普拉斯谱
定理7设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点边联图G1⊙G2的距离谱为
2) -2λ2j-2r2-2,j=2,3,…,n2;
5) 矩阵的四个特征值
证明由剖分点边联图的定义可知其距离矩阵D(G1⊙G2)可表示为
其中:Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
定理8设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点边联图G1⊙G2的距离拉普拉斯谱为

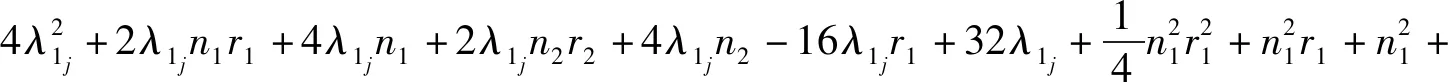

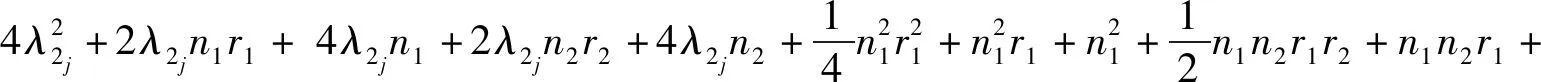
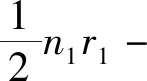
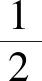
5) 矩阵的四个特征值
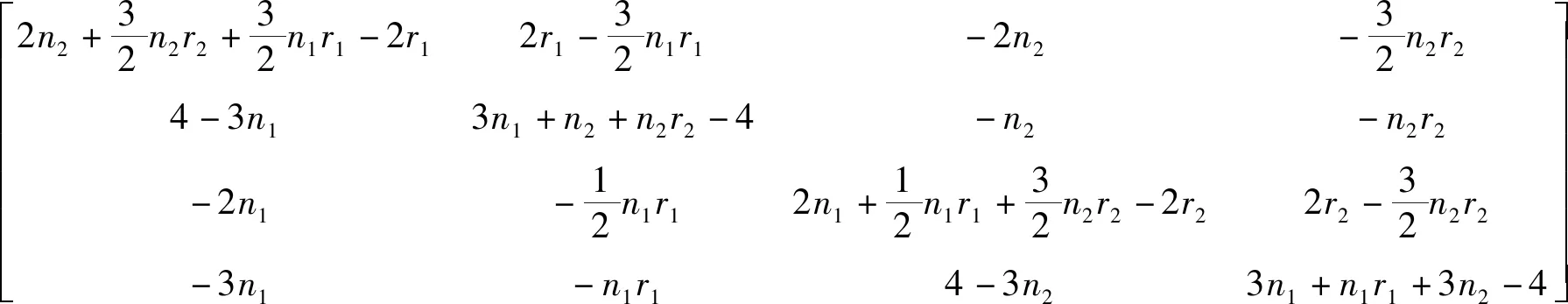
证明由剖分点边联图的定义可知其距离拉普拉斯矩阵DL(G1⊙G2)可表示为
其中
N7=3n1+n1r1+n2+n2r2-4
C5=(3n1+n1r1+3n2+2n2r2-4r2)I-4J+
2A(L(G2))
Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.
定理9设Gi是有ni个顶点的ri-正则图,其邻接矩阵A(Gi)对应的邻接谱为{ri=λi1,λi2,λi3,…,λini},i=1,2.则剖分点边联图G1⊙G2的距离无符号拉普拉斯谱为


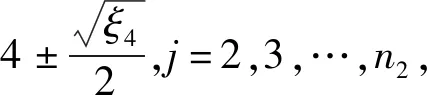
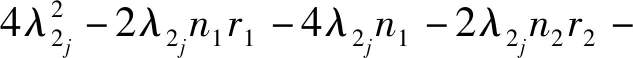
n1n2r1+n1n2r2+2n1n2-

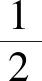
5) 矩阵的四个特征值
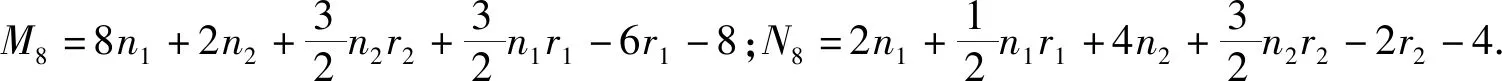
证明由剖分点边联图的定义可知其距离无符号拉普拉斯矩阵DQ(G1⊙G2)可表示为
其中
N9=3n1+n1r1+n2+n2r2-8
C6=(3n1+n1r1+3n2+2n2r2-4r2-8)I+4J-
2A(L(G2))
Ri是图Gi,i=1,2的关联矩阵;J为全一矩阵;I为单位矩阵.证明方法同定理1.

