拉回和推出的若干注记

何东林，李煜彦，彭康青

（陇南师范高等专科学校数信学院，甘肃陇南742500）

拉回和推出是环模理论、同调代数、代数表示论以及范畴论的基本概念之一，也是讨论模的投射性、内射性、平坦性以及各种同调维数等的重要工具，许多学者先后对其进行了研究[1-5]. 设R 为有单位元的结合环，本文主要针对具有特定形式左R-模的行正合交换图，给出拉回和推出的若干性质和等价刻画.

文中的环R 均指有单位元的结合环，模均指酉左R-模. 对任意左R-模同态和，记f 与g 的合成为其余涉及的概念和记号参见文献[6-7].

1 定义和引理

定义1[6]93设为左R-模的交换图，则：

1）称同态对(φ, α )是(φ, β )的拉回，如果对任意满足等式的同态对（其中且都存在唯一的同态使得且（此性质称为拉回的泛性质）.

引理1[6]96设( , )φ α 是( , )φ β 的拉回，则以下说法等价：1）若β 为单同态，则φ 为单同态；2）若β 为满同态，则φ 为满同态.

引理2[6]97设( , )φ β 是( , )φ α 的推出，则以下说法等价：1）若φ 为单同态，则β 为单同态；2）若φ 为满同态，则β 为满同态.

引理3[7]53设为左R-模的行正合交换图，则以下结论成立：1）当5t 为单同态且24,t t 为满同态时，3t 为满同态；2）当1t 为满同态且24,t t 为单同态时，3t 为单同态.

2 主要结论

定理1设为左R-模的行正合交换图，则以下条件等价：1）( , )φ α 是( , )φ β 的拉回；2）γ 为单同态.

证明 1）⇒2）. 设是的拉回.是包含同态，是Kerγ 的投射覆盖. 由是满同态及P 是投射模易知，存在同态使得因为是的拉回，考虑同态对由拉回的泛性质易知，存在同态使得由知，注意到且，可见又因为满同态右可消且μ为满同态，所以 0λ = . 而λ 为包含同态，因此γ 为单同态.

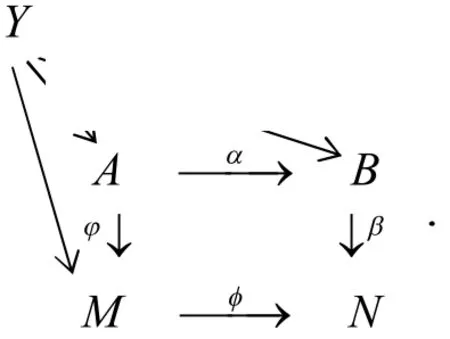
由定义1 知，(φ,α) 是(φ,β)的拉回.

对偶地，可得如下结论.

定理2设为左R-模的行正合交换图，则以下条件等价：1）),( βφ是),( αφ的推出；2）γ 为满同态.

由蛇引理可得以下推论，然而本文使用不同于蛇引理的方法给出其证明.

推论 1设为左R-模的行正合交换图，其中γ 为单同态，则β 为单同态当且仅当φ 为单同态.

证明⇒设β 为单同态. 由γ 为单同态及定理1 知，),( αφ是),( βφ的拉回. 根据引理1 可得φ 为单同态.

⇐设φ 为单同态. 将上图补充两个零同态可得如下行正合交换图

注意到φ 和γ 均为单同态，由引理3 易知，β 为单同态.

推论2设为左R-模的行正合交换图，其中γ 为满同态，则β 为满同态当且仅当φ 为满同态.

证明⇒设β 为满同态. 将上图补充两个零同态，由引理3 及γ 为满同态易知，φ 为满同态.

⇐设φ 为满同态. 由γ 为满同态及定理2 知，),( βφ是),( αφ的推出. 根据定理2 及引理2 易知，β 为满同态.

定理3设为左R-模的行正合交换图，且H 为任意左R-模. 如果γ 为单同态且HomR( H , β )为满同态，那么HomR( H ,φ)是满同态.

证明由假设γ 为单同态及定理 1 易知，(φ ,α)是(φ ,β)的拉回. 对任意f∈HomR( H , M),

因为HomR( H , β )为满同态，所以存在使得等式成立. 由拉回的泛性质可知， 存在同态使 得且. 从 而为满同态.

定理4设为左R-模的行正合交换图，且H 为任意左R-模. 如果γ 为满同态且HomR(φ ,H)为满同态，那么HomR(β ,H)是满同态.

证明由假设γ 为满同态及定理 2 易知， (φ, β )是(φ, α )的推出. 对任意f∈HomR( B,H),因为为满同态，所以存在使得fα=gφ. 又由推出的泛性质可知，存在同态，使得f σφ=且g σβ=. 从而也是满同态.