思有源 解有方*
●
(大和初中,四川 巴中 636031)
近期笔者遇到了一道解绝对值方程的题目,其常见的错误解法引发了笔者的深层次探究.
1 解法探讨
题目如果方程|3x|-ax-1=0的根是负数,那么a的取值范围是
( )
A.a>-3 B.a≥3 C.a<3 D.a≤-3.
(2016年初中奥林匹克数学竞赛试题)
1.1 错误解法
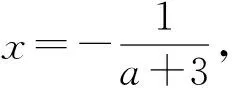
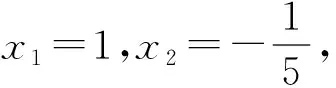
1.2 致错原因及思维突破
上述解法看似有根有据,其实迷惑性很强.为什么会出现上述结果呢?上述错误解法没有弄清绝对值方程的特殊性,机械套用了常规方程的处理方法.
对于本题,理解条件“根是负数”是关键.正确解题方法是克服思维定势的消极影响,在使用零点分类讨论的基础上,排除正根,即解决根的纯粹性问题;或利用数形结合思想,借助直观性突破思维障碍,或利用选项检验排除法获得正确答案.
1.3 正确解法
解法1(排除法)当方程的根是负数时,x<0,原方程为
-3x-ax-1=0,
即
(3+a)x=-1,
从而
3+a>0,
得
a>-3.
当方程的根是正数时,x>0,原方程为
3x-ax-1=0,
即
(3-a)x=1,
从而
3-a>0,
得
a<3.
可见,两个解集有公共部分,由于方程只有负数根,因此应从解集a>-3中排除a<3,结果为a≥3.故选B.
评注零点分类讨论是代数解法的基础,必须恰当使用:剔除不符合条件的部分.而上述错解中,解法并不完备,导致取值范围扩大.
思考1如果条件修改为“根是正数”呢?如果条件修改为“有一正一负根”呢?
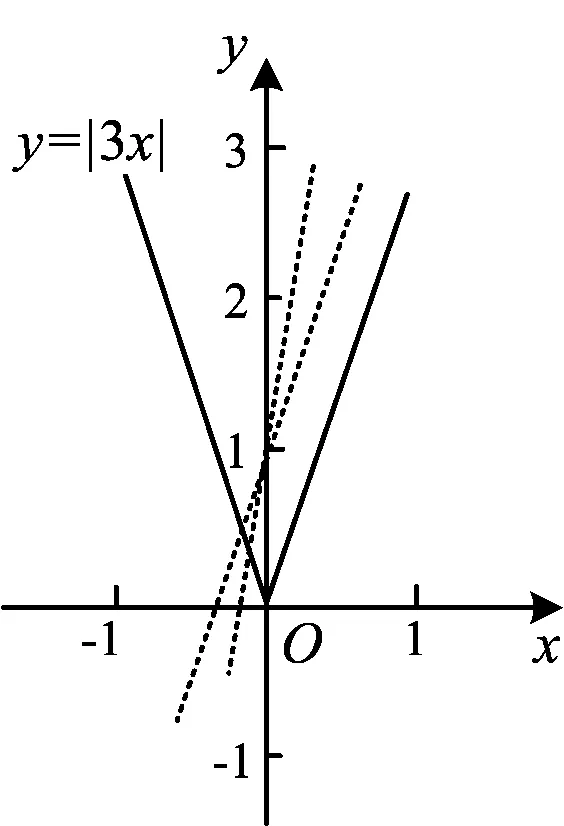
图1
利用上述零点讨论,对于前者应从解集a<3中排除a>-3,即a≤-3;对于后者应是两个解集的公共部分,即-3 解法2(数形结合法)如图1,作y=|3x|的图像,直线y=ax+1必过点(0,1).观察图像,当a=3时,直线y=ax+1与y=3x平行,并与直线y=-3x相交于第二象限,交点横坐标为负数,符合题意;当a>3时,直线y=ax+1与y=3x无交点,只与直线y=-3x相交于第二象限,交点横坐标为负数,符合题意. 综上所述,a≥3.故选B. 评注函数y=|3x|的图像关于y轴对称,经过定点(0,1)的直线与其相交,在y轴左侧有交点(对应根为负数)时,右侧可能有一个交点(对应根为正数),错误解法只考虑了负根有所欠缺. 从4个选项看,临界值有a=3,为提高区分度,再增加a=0,检验如下: 综上所述,选项B正确. 评注这种解法虽较为直接,但要增加区分度值作进一步检验,从而突破选项的迷惑性,避免偶然性的投机行为,提高排除法的准确性. 利用零点分类讨论,探究如下: 1)若b>0,当x>0时, x=kx+b, 从而 得 k<1. 当x<0时, -x=kx+b, 从而 得 k>-1. 关于x的方程|x|=kx+b(其中bk≠0):①有唯一正数根,应剔除有负数根条件,得k≤-1;②有唯一负数根,应剔除有正数根条件,得k≥1;③既有正数根,又有负数根,即有两个不相等的实数根,应取公共部分,得-1 2)若b<0,同理可得①当k<1时,有唯一正数根;②当k>-1时,有唯一负数根;③当-1≤k≤1时,无解. 思考2画出“V型”函数y=|x|和一次函数y=kx+b的图像,可以直观地得到上述结果(略). 先画出“V型”函数y=|x-a|和一次函数y=kx+b的图像,分类探究如下: |a-a|=ak+b, ③当-1 图2 图3 ①当k<-1或k≥1时,有唯一的根小于a; 图4 ③当-1≤k≤1时,没有实数根; ③当-1 ①当k>1或k≤-1时,有唯一的根大于a; ③当-1≤k≤1时,没有实数根; 请选择合适的方法解答以下3个例题. 例1已知方程|x|=ax+1有一个负根,且无正根,求a的取值范围. 解法1(零点分段讨论法)当x<0时,-x=ax+1,从而 得 a>-1. 当x>0时,x=ax+1,从而 得 a<1. 由于方程有一个负根且无正根,从解集a>-1中剔除解集a<1,得a≥1. 解法2(数形结合法)如图5,在同一坐标系中,分别作出y=|x|及y=ax+1的图像.直线y=ax+1过定点(0,1),因此a≥1. 解法3(运用结论)此处b=1,运用“关于x的方程|x-a|=kx+b(其中k≠0)根的性质”的相关结论,直接可得a≥1. 图5 图6 例2方程|x-2|+1=kx有两个不相等的实数根,求k的取值范围. 例3关于x的方程|x2-2x-3|=mx+1有正根,没有负根,则m的取值范围是 ( ) C.m>1 D.m<1 图7 解(数形结合法)如图7,在同一坐标系中作出函数y=|x2-2x-3|和y=mx+1图像,当直线y=mx+1经过点(-1,0)时,m=1.由于方程只有正根,没有负根,因此m>1.故选C. “千淘万漉虽辛苦,吹尽狂沙始到金”,科学探究离不开周密思考,只有去其糟粕,才能取其精华.通过“问题探究─归纳总结─应用升华”,定能实现数学学习和探究的不断超越.1.4 选项检验排除法


2 关于x的方程|x|=kx+b(其中bk≠0)根的正负性条件
3 关于x的方程|x-a|=kx+b(其中k≠0)根的性质
3.1 当a>0时的探究
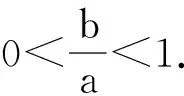
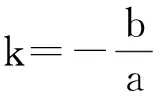
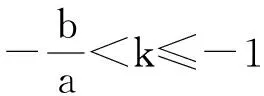







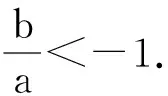



3.2 当a<0时的探究










4 解法应用