雪中梅花暗香来*——一道统测题的多解赏析

●

(源清中学，浙江 杭州 310015)

2018年1月下旬，浙江大地的一场大雪与“2017学年第一学期杭州市高三年级教学质量检测”不期而遇，大雪给杭州的考生增添了一丝寒意.好在数学试卷难度适中，多道考题透出新意，考后也值得回味，让考生感觉困难并愉悦着.这样的考题犹如雪中的梅花，寒风中透出的暗香，让人不忍离去.以下仅就其中的一道题为例加以赏析.

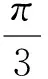
(2017学年第一学期浙江省杭州市高三年级教学质量检测数学试卷第17题)

题目简洁明了，求解内容也有别于常见的求平面向量的模或求平面向量数量积的问题，看到题目让人感觉耳目一新.考后笔者进一步品味、联想，感觉很有价值，与大家分享.

思路1直接入手很自然，再考虑相应函数的单调性.

解法1记f(λ)=λ+|a|,则

即当λ∈(-∞,0)时，f(λ)∈(-1,2),故λ+|a|的取值范围是(-1,2).

评注函数的取值范围(或最值或值域)问题，总是先考虑此函数的单调性，而导数正是解决函数单调性的有力工具.

思路2从向量的坐标形式也很容易入手.

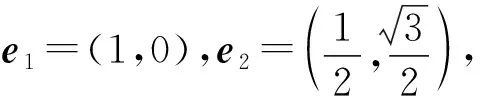
以下同解法1.

评注在平面图形中，若线段长为定值或角度已知，则往往建立平面直角坐标系进行分析，此情形下，向量的坐标形式就能发挥作用.

图1

思路3向量的几何背景往往令人耳目一新.

解法3如图1，显然，当λ=-2时，

|a|=|λ|=2；

当λ∈(-2,0)时，

λ+|a|∈(0,2);

当λ∈(-∞,-2)时，

|a|<|λ|,

从而

|OA|<|OM|,

过点A作AD⊥OM于点D，则

|DM|=1， |OA|>|OD|,

以O为圆心、OA为半径的圆交DM于点E，此时

λ+|a|=|a|-|λ|=-|EM|∈(-1,0),

故

λ+|a|∈(-1,2).

评注向量是几何与代数的交汇区，向量的运算有着浓厚的几何背景，数形结合的思想在平面向量中得到最充分的体现[1]，是培养学生数形结合思想的很好机会.在解决向量问题时，首先想到的是它的几何意义.

思路4在△AOM中，|AM|=2，另两边可以通过一个变量进行表示，这是三角的优势.

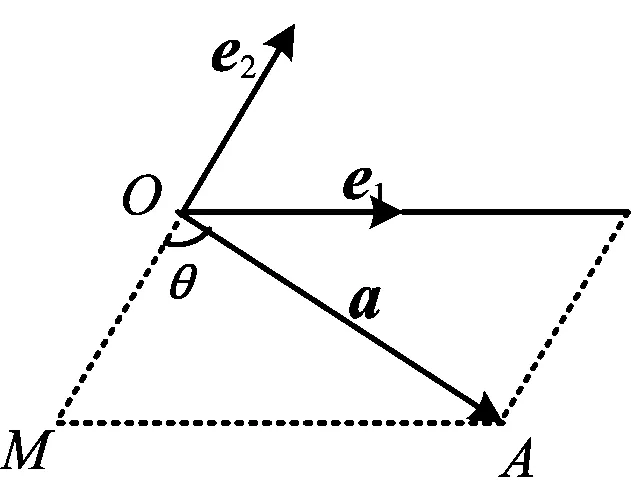
图2

于是

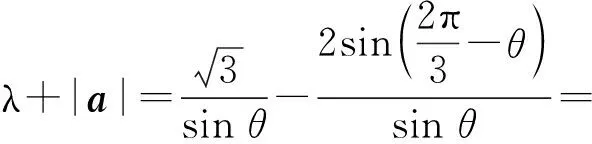
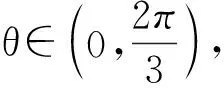
于是

λ+|a|∈(-1,2).

思路5函数问题的三角代换往往很有效.

由λ2+2λ+4=(λ+1)2+3≥3,可设

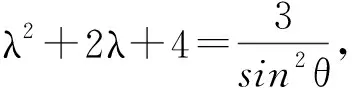
则

当λ+1>0,即-1<λ<0时，

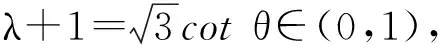
当λ+1<0,即λ<-1时，

从而

即

综上所述，当λ<0时，λ+|a|∈(-1,2).

评注三角代换主要是利用丰富的三角公式，将相对比较复杂的代数式转化为容易处理的三角式，通过有界性达到求取值范围的目的.对于双变量的问题，三角代换的效果往往较好.

思路6双变量问题也可以转化为圆锥曲线考虑.

t2-(λ+1)2=3,

即

上述方程所表示的曲线C是双曲线右支的一部分(如图3)，此时z=λ+t，即斜率为-1、λ轴上的截距为z的直线l[2]，直线l与上述曲线C有公共点时，l需介于两平行线l1与l2之间，故

-1

即

λ+|a|∈(-1,2).

图3 图4

思路7根式与距离“有缘”.

|AM|-|OM|.

在△OAM中，

|AM|-|OM|<|OA|=2,

记点A在x轴上的投影为点B，则当λ→-∞时，|MB|→|MA|,从而

|AM|-|OM|= |AM|-(|MB|+|BO|)>

-|BO|=-1,

故

评注根式、绝对值有明确的几何意义，在代数问题中联想几何意义，其解法真可谓是赏心悦目.

思路8向量数量积的坐标形式可以巧妙运用.

图5

z=m·n-1,

注意到

易得m·n∈(0,3),从而

z=m·n-1∈(-1,2),

即

λ+|a|∈(-1,2).

思路9换一个角度，变量换位更巧妙.

则

即

由λ<0,得

-1

根据三角形两边之差小于第三边知z<-2不符，应舍去.故λ+|a|∈(-1,2).

评注在双变量或多变量问题中，当直接入手有困难时，转换角度、变量换位是一种很好的方法，可能会给我们带来惊喜.

此题变量多，有一定的思维要求，学生感觉不容易处理.如果我们能展开联想，打开思路，多进行尝试，那么就会得到不小的收获.

解法1记a2+b2=r2，试一试三角代换，令

其中θ∈R.由已知，关于x的方程

有实数解，即关于x的方程

有实数解，得

故

即

从而

于是

即

解法2由题意可知关于x的方程

有实数解.

试一试变量换位，联想双变量的转化策略，上述方程可看作是以(a,b)为坐标的平面直角坐标系aOb中的直线方程，而a2+b2则是此直线上的点到原点距离的平方.由点到直线的距离公式，得

以下同解法1.

结束语一道测试题，内容可以涉及到现行高中数学中数形结合最充分的函数、三角、平面向量、解析几何等内容，其丰富多彩的思维角度和解题方法，给考生以宽阔的意境空间，体现了该题深厚的内涵，如此具有匠心的设计，不得不让我们对命题者肃然起敬.高三学习是辛苦的，优质的试卷和试题，通过教师的思维引导和解法展示，资源得到了充分利用，可以减少学生的疲劳感，既能达到训练的目的，又可以适度减轻学生的负担，更能对学生的心理疏导起着良好的作用.这样的好题不禁让我们想起了严寒雪天中的梅花，真所谓“雪中梅花暗香来”啊！

参考文献

[1] 曹凤山.一个向量模 年年高考题[J].中学教研(数学)，2017(12)：43-46.

[2] 孔胜涛.让解题思路因联想而“自然”——一道高考题的解法探究与拓展[J].中学教研(数学)，2018(1)：14-16.