“单位圆定义法”与“终边定义法”的有机融合*——以3节“任意角的三角函数”课堂实录为例

●

(内江师范学院数学与信息科学学院，四川 内江 641199) (伍隍中学，四川 资阳 641300)

2017年11月27日，首都师范大学博士生导师王尚志老师、北京理工大学附属中学关健老师应邀到四川师范大学附属中学(高中部)参加“核心素养导向的高中数学研修活动”．研修活动之一为“任意角的三角函数”同课异构，分别由四川师范大学附属中学的李兴福老师、北京理工大学附属中学的关健老师执教．下文拟从这两节课中提出两个引发笔者深思的问题．

1 课堂实录

1.1 课堂实录1

四川师范大学附属中学使用的教材是人教A版《数学(必修4)》，其中“任意角三角函数”是利用单位圆定义的，简称“单位圆定义法”．李老师的教学流程如下所示：

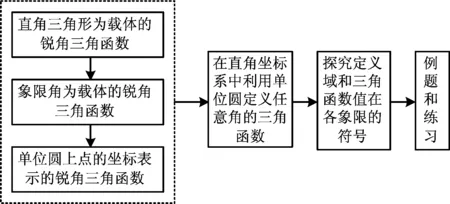
在例题和练习这一环节中，李老师请学生独立思考并解答例1，课堂实录呈现如下：

例1已知角α的终边经过点P0(-3,-4)，求角α的正弦、余弦和正切值．

师：好，稍等，你是如何求出角α的正弦值的？

生1：根据点P0的坐标(-3,-4)算出单位圆半径r=5．

师：单位圆的半径能不能等于5？

生(略带笑意并大声回答)：不能．

师(追问)：那单位圆的半径为多少？

生(齐答)：单位圆的半径为1．

(此时下课铃声响起，李老师请另一位学生对此题进行补充.)

图1

(李老师简单点评，并介绍根据相似可用平面几何的知识解答此题．最后伴随着一个问题的提出，结束本节课.)

师：以后遇到点P不在单位圆上的问题，是否都要对其进行转化呢？大家能不能将其推广到一般情况，即对于终边上任意一点P(x,y)，如何来表示它的正弦、余弦和正切？

1.2 课堂实录2

关健老师通过4个层层递进的问题推动教学．教学流程如下所示：

图2 图3

2 引发思考

根据以上课堂实录，引发笔者提出如下两个思考：

1)单位圆的半径是否为1？

人教A版《数学(必修4)》中单位圆的定义为：在直角坐标系中，称以原点为圆心、以单位长度为半径的圆为单位圆[1]．

何谓单位长度，百度百科解释为：一个单位的长度．单位长度就是可供参考的标准，它没有固定值，依设定而变动，不是实际的长度计量单位．但是根据教材第12页图(如图3)中点A的坐标为(1,0)，可以推导教材在此处默认单位圆的半径为1，即默认单位长度为1．

因此教材在静态地呈现数学知识时，应该严谨——既要考虑到学生认知发展水平的有限性，又要保证知识的可发展性，如单位圆对后继学习拓扑学、复变函数论等的影响．

2)怎样将“单位圆定义法”与“终边定义法”有机融合？

人教A版《数学(必修4)》中的例1有让学生研究“终边定义法”的意图，李老师在认真钻研并仔细揣摩教材编写意图后，使例1较好地完成了它的使命．只是学生在解答例1的过程中，出现了“不按常理出牌”的“小插曲”．

当然欲将两种定义法有机融合，并不完全是因为“单位圆定义法”不利于解题，而是因为两位教师分别用“单位圆定义法”和“终边定义法”给出“任意角三角函数”的定义，致使笔者大胆猜想：为何不将这两种定义法有机融合呢？

在完成用直角坐标系内点的坐标表示锐角三角函数后，只需要再适当引导学生完成从锐角到任意角的突破，实现用点的坐标表示任意角的三角函数(即“终边定义法”)已经呼之欲出，最后再根据相似，引导学生取适当点的位置，简化三角函数定义中的表达式．自然合理地实现从“终边定义法”到“单位圆定义法”的过渡，这样做既不会削弱用单位圆上点的坐标定义任意角三角函数的优点，又可以绕过通过例1(实际教学中学生往往感觉吃力的例题)来引入“终边定义法”的圈子．

3 教学实施建议

为了实现“单位圆定义法”与“终边定义法”的有机融合，笔者尝试着调整人教A版中“任意角三角函数”的教学流程如下：

3.1 调整教学流程

人教A版《数学(必修4)》中定义任意角三角函数的流程如下：

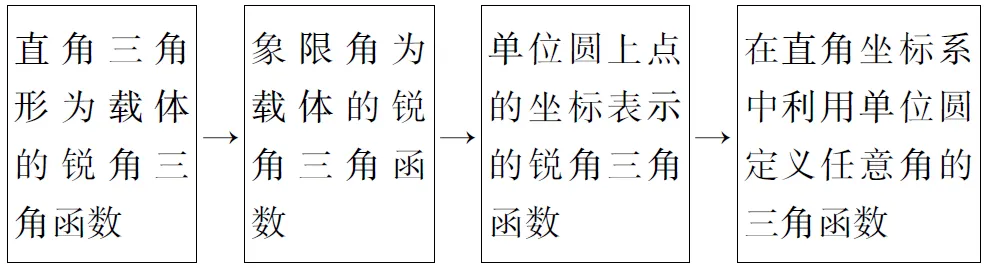
笔者在认真研读、对比人教A版和苏教版“任意角三角函数”的内容后，结合2013年江苏省中小学数学研究室、名师课堂直播活动中的课堂视频[2]，即扬州大学附属中学的陆萍老师执教的“任意角三角函数”课例,将教学流程作出如下调整：

3.2 教学实施建议

生(众)：α，y，r．

师：如果角α确定了，其终边也就确定了，那这条终边上有多少个点呢？

生(众)：无数个．

师：每一个点Pi都有其对应的坐标(xi,yi)和到原点的距离ri，那sinα的值是不是也有无数个呢？

生1：等式是成立的，sinα的值只有一个．我们可以通过相似三角形来解决这个问题．

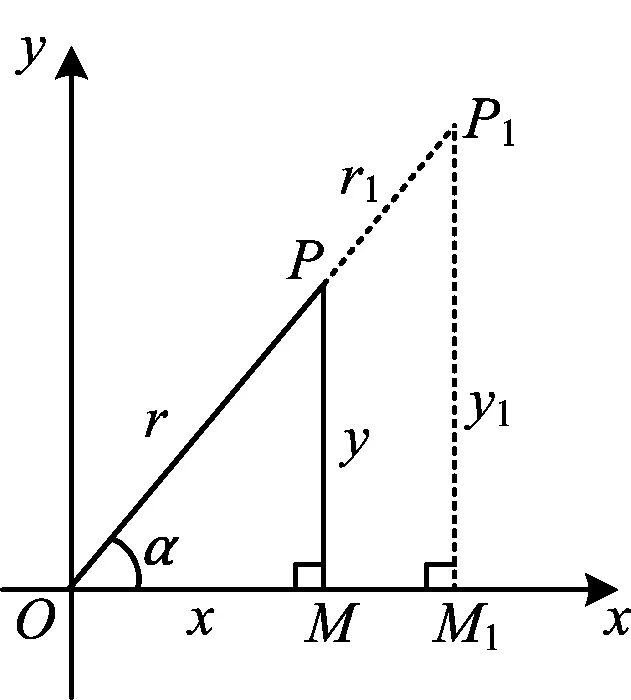
图4

师(提示)：如果在一个数集当中对任意一个元素，在另一个数集当中都有唯一确定的元素与之对应．这是什么对应关系？

生(众)：函数关系．

设计意图教师应注意引导学生明白：角α既是一个角，又是一个实数(弧度数)．因为在弧度制下，角的集合与实数集R之间建立起了一一对应的关系，这样才能与函数定义中的“两个非空数集”保持一致．

生2：是的．

师：那角α的终边表示的角有多少个？

生2：无数个．

师：怎么表示？

生2：α+2kπ,其中k∈Z．

设计意图此处学生已出现从锐角过渡到任意角的认知障碍，教师应及时给予正确的疏导，通过对学生错误的质疑和释疑，巧妙地将其转化为“美丽的错误”．

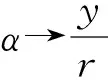
师：当角α的终边落在第二象限时，如图2，是否也存在这样的对应关系？

设计意图通过图2的直观呈现，以“形”刺激，突破学生认知图式中锐角的局限．

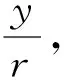
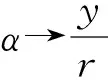
生4：因为我看出它与三角有关系，所以我们可以称它为三角函数．

师：那更具体一点呢？当α为锐角时，我们称它为什么？

生4：锐角三角函数，如果锐角扩展到任意角的话，我们可以称它为任意角的三角函数．

问题5当α为任意角时，能否依然延用这种符号和名称呢？

生4：可以．

生(众)：能．

设计意图教师低调、轻松的风格，让学生不会因为不熟悉的符号而畏缩，不会感觉好像在受数学的“威胁”．

师：请同学们观察上述3个等式，有什么需要注意的地方？

(此时教师鼓励学生类比、联想锐角三角函数，尝试主动建构任意角三角函数的概念.)

以上是借鉴汲取文献[2]中陆萍老师的课堂实录，实现了“终边定义法”下的任意角三角函数概念的建构．下面进行“单位圆定义法”与“终边定义法”的无缝连接．

问题6能否通过取适当点P，将任意角三角函数定义中的表达式简化？

生6：如果r=1，此时sinα=y，cosα=x，即角α的正弦值等于点P的纵坐标，角α的余弦值等于点P的横坐标．

设计意图教师引导学生对比发现，当取r=1(即到原点的距离为1)时，能简化表达式，体现简约思想，并为引出单位圆奠定基础．

定义单位圆在直角坐标系中，称以原点O为圆心、以单位长度为半径的圆为单位圆．

利用单位圆可定义任意角的三角函数如下：

任意角的三角函数定义[3]如图3，设α是一个任意角，它的终边与单位圆交于点P(x,y)，那么

1)y叫做α的正弦，记作y=sinα，即sinα=y；

2)x叫做α的余弦，记作x=cosα，即cosα=x；

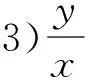
设计意图采用弧度制度量角，就是用单位圆的半径来度量角，这时角度和半径长度的单位一致，这样，三角函数就是以实数(弧度数)为自变量、以单位圆上点的坐标(也是实数)为函数值的函数[4]．需要特别指出的是，此定义完善了人教A版《数学(必修4)》中任意角三角函数定义的两个小瑕疵，详见文献[3]．

4 结语

本文结合来自四川、北京、江苏3位名师具有代表性的3节“任意角的三角函数”课堂教学实录，提出将两种定义方法有机融合的教学实施建议，使其更符合学生的认知发展规律，有利于学生建构其知识结构图，从而真正理解概念的本质．

数学教学需要问题来驱动，数学思维需要问题来发动，数学灵感需要问题来触动[5]．因此在数学教学中设计具有逻辑性、生成性、层次性的问题串，是学生享受数学乐趣的切入点．数学问题有了逻辑性，这些问题才是合理的、自然的，学生才能效仿、尝试着提出新的问题，并且愿意去解决这些问题；数学问题有了生成性，学生在一个初始问题的引导下，才会顺着自然的思路、逻辑的框架，提出一系列问题；数学问题有了层次性，学生在不同层级问题间的跨级和交换，才会实现从具体的操作向数学思想方法、数学观念之间的跨越．这样的数学课堂，学生才拥有了参与数学活动的主动权，才拥有了“吾思故吾在”的感悟，才感受到自己最直接的价值，感受到生命，感受到快乐．

参考文献

[1] 刘绍学，钱珮玲，章建跃，等．普通高中课程标准实验教科书·数学(必修4)(A版)[M]．北京：人民教育出版社，2007．

[2] 陆萍．高中数学名师课堂：任意角的三角函数[EB/OL]．2017-12-27．https://www.ixigua.com/i6495641726386962957/?utm_source=toutiao&utm_medium=feed_stream#mid=71675369193．

[3] 王佩，赵思林．对人教A版高中数学教材中几个问题的商榷[J]．教学与管理:中学版，2018(2)：42-44．

[4] 章建跃．为什么用单位圆上点的坐标定义任意角的三角函数[J]．数学通报，2007，46(1)：15-18．

[5] 王佩，赵思林．基于问题驱动的数学教学设计——以“任意角的三角函数”为例[J]．中学数学月刊，2017(10)：17-20．