“算法”视角下解析几何综合题教学的尝试与思考*

●

(南京师范大学附属扬子中学,江苏 南京 210048)

针对解析几何综合题的教学，笔者所在备课组进行了一次集体备课，集思广益.备课组成员畅所欲言，对目前学生解决解析几何综合题的现状、困惑进行了梳理总结，同时提出了解析几何综合题的教学建议以待课堂实践.作为备课组长的笔者率先垂范，首先开了一节课供大家进行研讨，以求进一步优化教学.通过这一阶段的教学研讨，大家一致认为在解析几何综合题的复习方面取得了良好的效果.本文就笔者开设的一节课谈谈“算法”视角下的解析几何综合题教学的实施策略,不妥之处还望广大同行批评指正.

1 现状与困惑

大多数学生对于解析几何综合题的认识比较片面，他们普遍认为解析几何综合题难度大、计算量大,即使考试时遇到会做的题目，考场上也没时间算到底，最终还是拿不到分.因此,他们不愿意在这方面投入更多的复习时间.若遇到容易题，大家都能解出来，区分度不大，总之认为花费太多的时间不值.学生畏难情绪严重，不愿意深入思考，讨厌复杂运算，这直接制约着解析几何综合题的复习效果.教师方面，对解析几何综合题教学也没有好的方法，教师直接讲(或对答案)、学生板演(或投影学生的解题过程)教师点评、教师点拨解题思路后让学生运算等等.一节课讲不了几道题(有时一道题也讲不完),对学生掌握的情况也不甚了解，课堂乏味，效率低下.

2 问题与对策

问题出在哪里呢？

数学教育对于个人成长与社会进步的主要作用就是促进学生思维的发展.特别是，教师应当帮助学生通过数学学习逐步学会更清晰、更深入、更全面、更合理地进行思考，从而不断提高自身的思维品质，并能真正成为一个高度自觉的理性人[1].

教学生学会思考，发展学生的认知力，这是数学教学的根本目标.因此解析几何综合题教学的主要问题在于没有把“教会学生思考”作为核心问题来抓，而是片面地认为繁琐计算成了解题的拦路虎.引导学生深入思考、优化计算理应成为解决解析几何综合题的突破口.针对这些问题，我们备课组提出了让思考先行，从“算法”的视角优选参变量的教学策略.如何操作呢，我们先来看一段课堂实录.

3 课堂实录

以下是笔者所开设的一节课的教学片段：

1)求椭圆C的方程.

2)如图1，设A为椭圆的上顶点，过点A作两条直线AM，AN，分别与椭圆C相交于点M，N，且直

线MN垂直于x轴．

①设直线AM，AN的斜率分别是k1，k2，求k1k2的值.

②过点M作直线l1⊥AM，过点N作直线l2⊥AN，l1与l2相交于点Q．试问：点Q是否在一条定直线上？若在，求出该直线的方程；若不在，请说明理由．

师：请同学们自主解决第2)小题第①问.

师：请一名同学叙说解题思路.

师(投影展示解题过程)：非常好！生1认为“动”的根源是两直线的斜率在变化，因此可以选取斜率作为参变量进行解题，借助韦达定理及点M与N的对称性建立关系式来解决.有没有不同的解法？

师(投影展示解题过程)：非常棒！生2认为“动”的根源是点M的变动，因此选取点M的坐标作为参变量进行解题.结合点M在椭圆上可以得到相应的关系式，进而求解.

多数学生还是选择了第一种做法，思路常规，容易想到，算法流畅，由于计算量不大，绝大多数学生都解出来了.

师：两种方法都非常好，但从计算量的角度看孰优孰劣一目了然.之所以出现计算量不同，归根结底和我们选取的参变量有关.我们求解解析几何综合题的最大担忧就是计算量，看来优选参变量是优化解题的突破口.

启示1从教师的层面看，每个教师应该有个人教学特色的例题讲解范式，针对不同类型不同难度的题目再作适当调整.本题启示我们应引导学生进行多角度审题，基于题目条件进行多视角处理，预设解决本题的多种算法，比较不同算法的优劣，选取最恰当的策略尝试解题，如此思考会给解题带来意想不到的效果.

师：有了刚才的总结，请思考第2)小题第②问的参变量选取，然后预设解题算法.

师：请一名同学叙说求解该题的算法.

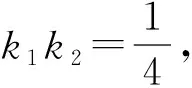
师：还可以选择其他变量解决吗？

生3：感觉这种方法解题比较流畅，可能运算量要大一些.

师：非常棒！一会给大家时间去运算.有没有其他选取变量的方法？

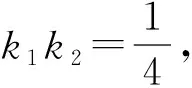
师：思路倒行得通，运算量不小.还有其他想法吗？

生5：可以假设点Q的坐标，利用垂直关系建立关系式，用斜率和向量都可以.这样做可以回避联立方程组求点Q的坐标，从而减少计算量.

师：以上3位同学已经提供了解决该题的3种算法，相信还有不同的求解算法，请你比较一下，选择一个你认为最简单的方法来解决.

教师巡视学生的解题情况并选择几种不同的方法投影展示，讨论比较.通过联立两直线方程，求点Q的坐标，得到yQ=-1，只有2位学生算出，其他学生没有算完，看来运算较繁.利用假设点Q坐标求解的学生，基本都求出了结果，没得到结果的也化简到了最后一步,运算量不大.

教师板书示范完整的解题过程，如下：

设M(x0，y0),Q(x1，y1)，则N(x0，-y0)，依题意可得A(0，1)．

因为l1⊥AM，所以

即

(y0-1)(y1-y0)=-x0(x1-x0).

又因为l2⊥AN，所以

即

(-y0-1)(y1+y0)=-x0(x1-x0),

故

(y0-1)(y1-y0)-(-y0-1)(y1+y0)=0,

化简得

(y1+1)y0=0.

因为点M是动点，所以y0是变量，不可能恒为0,从而

y1+1=0，

即

y1=-1,

故点Q在定直线y=-1上．

师：本题的目标是点Q的坐标是否满足一定直线方程，因此目标引导我们解题时要寻求点Q的坐标满足的关系式.因此直接设坐标比求坐标要来得快.

启示2从题目本身的层面看，解题首先要明确题目结论的本质.教师要引导学生养成“让结论引导思考”的思考范式.本题启示我们应引导学生先对题目的结论进行多角度分析，锁定结论目标进行多视角处理，预设解决本题的多种算法，比较不同算法的优劣，选取最恰当的策略尝试解题.

4 教学反思

《普通高中数学课程标准(2017年版)》教学评价与建议部分指出：教师要把教学活动的重心放在促进学生学会学习上，积极探索有利于促进学生学习的多样化教学方式，引导学生总结出一些具有针对性的学习方式[2].解析几何综合题作为高中数学综合题的典型代表，其教学范式也值得借鉴和迁移.

4.1 探寻条件中“动”的根源，优选参变量

解析几何综合题的特点是离不开“动”，点动、线动或量动等等.认识“动”的根源，寻求解题突破口.点动或线动最终都要用变量来进行刻画，选取不同的参变量就会有不同的思路、不同的计算量、不同的处理方法，孰优孰劣能预先判断为好.因此选取合适的参变量(解析几何中常见的参变量有斜率、点坐标、角等)是优化解题的根本所在.基于此，我们的处理策略是：先深入理解题意，结合题目条件，对可用参变量都预设解决本题的一个算法(即拟定一个解题方案)，从而预知哪一步可以出现哪些量、可以求出哪些量、可以消去哪些量、哪一步用到什么方法、出现什么式子及计算复杂程度等等，然后对每一个算法的复杂程度与运算量进行比较，选取最佳参变量尝试解题.

4.2 锁定结论中目标导向，优选参变量

解题过程其实就是先认识“我在哪里”(题目条件)要“到哪里去”(结论)，其次是探寻“如何去”(解题策略)的问题，让“要到哪里去”引导我们去思考“如何去”的问题.因此解题要锁定结论中的目标导向，然后去设计求解策略.基于此，我们的处理策略是：先深入理解题意，锁定题目结论，明确要求什么量或式子，需要引入哪些参变量可以实现，对可用参变量都预设解决本题的一个算法(即拟定一个解题方案)，比较分析，尝试解题.

高中数学综合题的解题就是一个不断探索、尝试、调整、修正、优化的过程.这个过程既有对条件的多角度转化，同时也离不开结论的目标导向.解析几何综合题具有思考量大、逻辑性强、计算量大等特点，是从“算法”的角度来思考问题的典型素材.从“算法”的角度思考问题的方法也可以迁移到解决其他综合题上，让思考先行，少走弯路，事半功倍.其思考过程可以归结如下所示：

波利亚的《怎样解题》明确指出解题四部曲：理解题目、拟定方案、执行方案、回顾[3].如果我们能从“算法”的角度预设几个解题方案，先比较优劣，再优选方案，岂不更好？优化解决一道题的同时发散了我们的思维，对题目的认识更深刻.坚持从“算法”的角度思考问题，养成良好的思考习惯和认知习惯，定能厚积薄发.

参考文献

[1] 郑毓信.数学教育的“问题导向”[J].中学数学教学参考，2018(1/2):2-6.

[2] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京：人民教育出版社，2018.

[3] 波利亚.怎样解题[M].涂泓,冯承天，译.上海：上海科学技术出版社，2016.