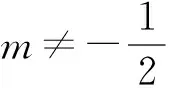不单调三次函数图像中矩形性质的探究*

● ●

(正始中学,浙江 宁波 315131) (宁波市教育局教研室,浙江 宁波 315000)

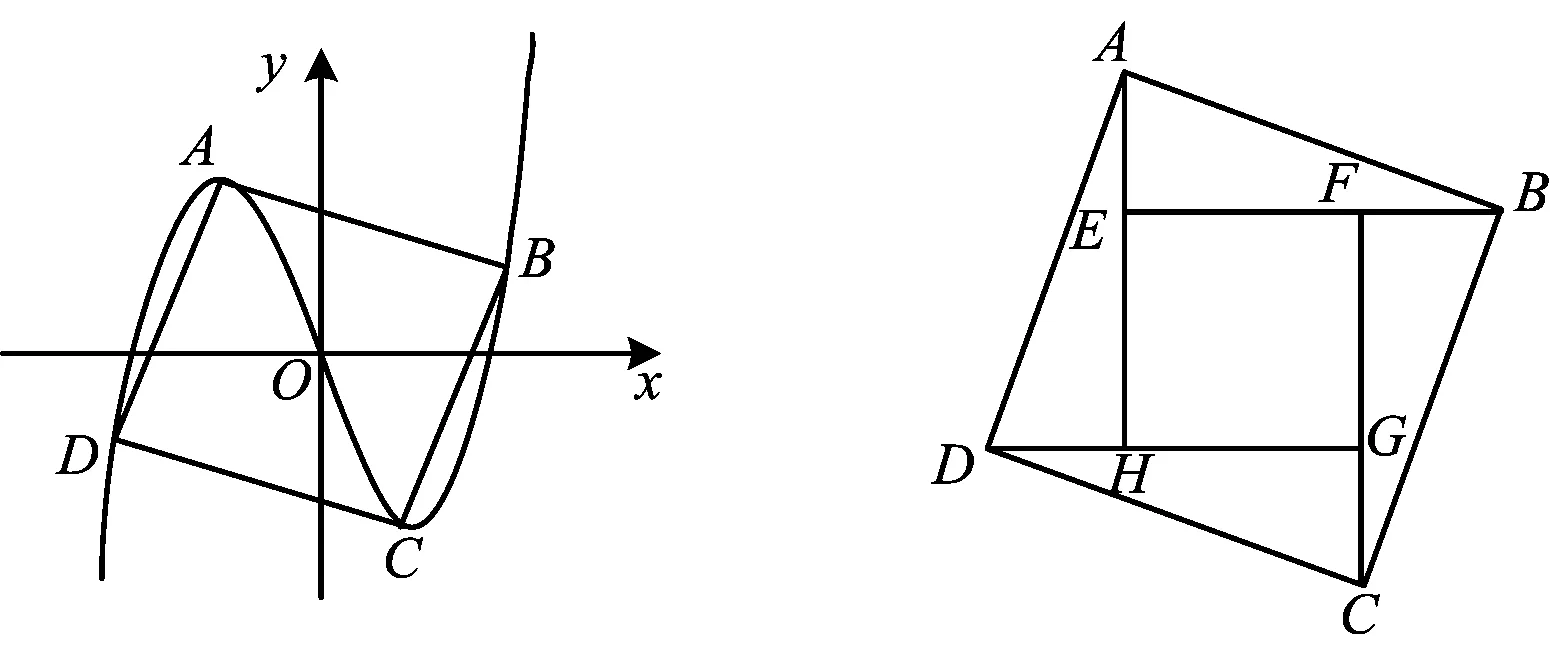
笔者在教学三次函数图像与性质时，想到如下问题：不单调的三次函数分别以两个极值点为切点作切线与三次函数图像有两个交点，以这两个交点为对角线构成的矩形与三次函数图像有什么关系?为了说明简便，令三次函数f(x)=ax3+bx2+cx+d，由于对a>0与a<0的两种情况研究方式类似，因此本文只研究a>0的情形．

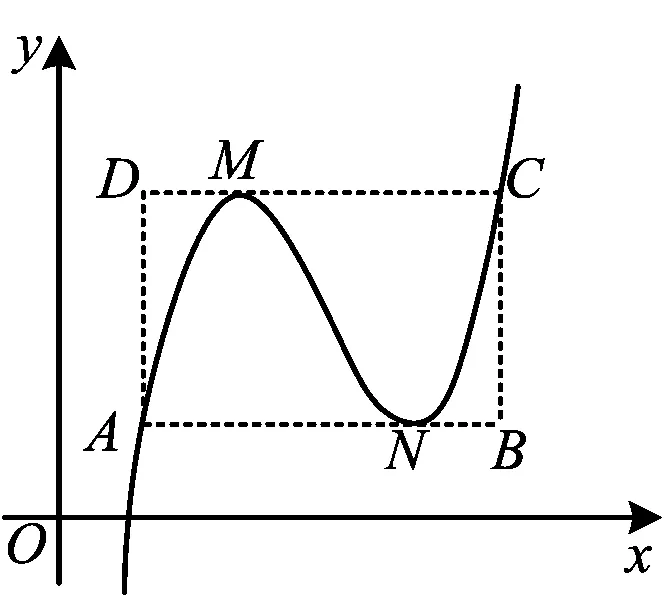
图1

1 预备知识

1.1 定义矩形

当三次函数f(x)=ax3+bx2+cx+d(其中a>0)在R上不单调时，f′(x)=3ax2+2bx+c的判别式Δ=4(b2-3ac)>0，导函数有两个不相等的零点x1,x2(其中x10)的矩形．

1.2 简化形式

对三次函数f(x)=ax3+bx2+cx+d(其中a>0)进行配方，得

g(x)=ax3-c0x.

2 探究矩形的一些结论

定理1不单调的三次函数过两个极值点分别作切线与三次函数图像有两个交点，以这两个交点连接线段为对角线构成矩形，则两个极值点分别是这个矩形边上的四等分点．

图2

证明令三次函数g(x)=ax3-c0x(其中a>0,c0>0)．由

g′(x)= 3ax2-c0=

知

因为函数f(x)可由函数g(x)平移得到，所以两个函数的矩形大小相同，且对应点之间的比例关

系不变，于是

1)在不单调三次函数f(x)=ax3+bx2+cx+d(其中a>0)中，由图2知xA,xM,xO,xN,xC成等差数列，令等差数列的公差为H，根据定理1易得

2)设不单调三次函数的中心坐标为P(x0,f(x0))，则f(x0-d)=f(x0+2d)均等于极大值，f(x0+d)=f(x0-2d)均等于极小值．

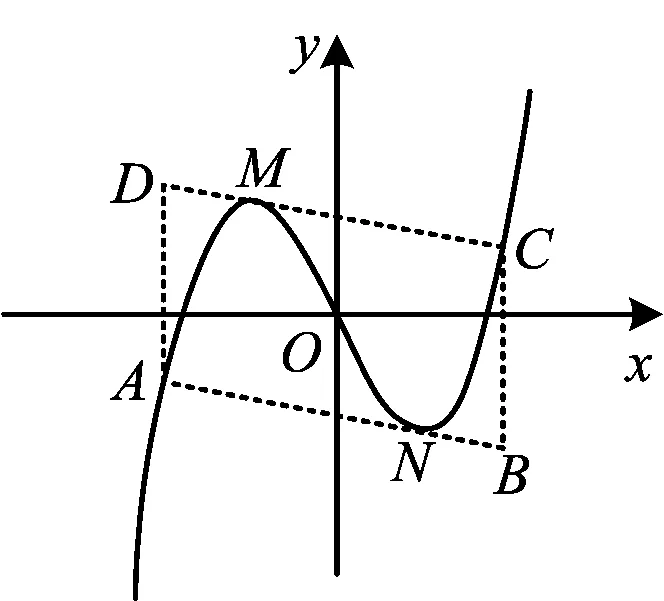
图3

推论1已知不单调的三次函数g(x)=ax3-c0x，如图3所示，过曲线上两个点M,N分别作切线与三次函数图像交于点A,C，且CM∥AN;过点A,C作竖线交切线于点B,D构成ABCD，则两个切点M,N分别是这个平行四边形边上的四等分点．

证明函数g(x)=ax3-c0x(其中a>0,c0>0)的图像如图3所示，则

g′(x)=3ax2-c0.

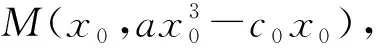
与g(x)=ax3-c0x联立，得

解得x=x0或x=-2x0，即xC=-2x0.由对称性可得xD=xA=2x0,易得M为DC的四等分点．又由对称性可知N为AB的四等分点，故两个切点M,N分别是这个平行四边形边上的四等分点．

推论2如果不单调的三次函数为g(x)=ax3-c0x，那么参数c0决定矩形的形状(即水平的长与垂直的宽之比)．

矩形的水平边长与垂直边长之比为

图4

3 c0取特殊值时的几个结论

1)当c0=3时，“一个矩形”是正方形；

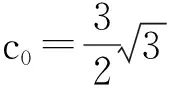
利用不单调的三次函数图像中矩形的性质定理和推论不难证明以上结论，具体请读者自行完成证明．

4 应用举例

例1已知函数f(x)=x3+(m+2)x2+(2m+1)x(其中m∈R),设函数f(x)除0外还有两个不同的零点x1，x2(其中x1x2≠0，且x1f(-4)恒成立，求实数m的取值范围．

解由题意得

f(x)=x·[x2+(m+2)x+(2m+1)]，

可知x1,x2是方程x2+(m+2)x+(2m+1)=0的两个不相等的非零根，于是

Δ=(m+2)2-4(2m+1)>0，

1)当m>4时，

从而

x1

综上所述，实数m的取值范围是

例2如图5，已知函数f(x)=x3-mx，直线l1∥l2，l1与函数f(x)的图像切于点A,交于点B;l2与函数f(x)的图像切于点C,交于点D,若四边形ABCD为正方形，求m的值．

图5 图6

即

例3设与x轴平行的两条直线l1,l2与函数f(x)=x3+ax2+bx+c的图像各恰有两个公共点.证明：以这4个点为顶点的四边形为菱形的充要条件是这个四边形的面积为6.

(2015年保加利亚国际高中数学竞赛试题)

图7 图8

证明平移函数图像，使得AC的中点为原点(如图7)，构成新的函数

构建三次函数矩形(如图8)．

必要性：由推论2可得

又由三次不单调函数图像中矩形的性质定理可得A为BE的四等分点，则

已知四边形ABCD为菱形，从而

解得

即

解得

则

从而

充分性：已知S四边形ABCD=6，则

即

解得

此时

即kBD·kAC=-1，故四边形ABCD为菱形．

综上所述，以这4个点为顶点的四边形为菱形的充要条件是这个四边形的面积为6．

从上面问题的发现、提出、分析和解决的过程之中能充分感受到数学的简约美、严谨美、对称美与和谐美[1]．

参考文献

[1] 任伟芳.历经三重境界探究椭圆性质的一个案例[J].中学教研(数学)，2013(10)：23-26．