关注效率，提升能力

施磊倩

[摘  要] 在初三的二轮复习中，学生的学习时间已经进入倒计时状态，效率成为最后冲刺的生命线，如何提高效率成为我们复习课的关键所在. 题目的精选、精讲，变式的训练、挑战，方法的点拨、提炼将开启高效复习课堂的新征途.

[关键词] 效率;数学;二轮复习;复习课

复习课是初三教学的主要课型， 二轮复习介于一轮的基础回顾和三轮的综合训练之间，是提高学生能力的重要过程. 如何提高二轮复习的效率，更好地服务于学生？如何通过二轮复习提高学生的解题能力，让学生的成绩得到更稳定和持久的提高？这是一线教师经常思考的问题. 本文就如何进行二轮复习谈谈自己的看法，供各位参考.

精挑细选，凝练精华

二轮复习通常以专题为主，选择哪些内容作为专题？选定多少个专题？这是二轮复习之前初三数学教师们需要斟酌的问题. 笔者认为，因二轮复习时间较短，通常仅有一个月，因此专题的选择不宜太多、太细，否则一方面由于时间的限制无法完成，另一方面不利于学生形成综合运用知识的能力. 因此，专题要精挑细选，根据自己学校和本班级的实际情况及学生对知识的接受能力，将“精华”浓缩于6～8个专题. 如笔者所执教的初三年级（人教版）经过与备课组的协商之后将专题敲定于“数与式”“方程与不等式”“函数及图像”“图形与变换”“动点问题常见题型和解题方法”“图表信息类问题”“几何最值问题常见题型和解题方法”“数形结合思想在实际问题中的运用”这八个. 每个专题的例题同样需要筛选，其中以专题“方程与不等式”为例，选取了以下几个例题：

这三个例题是方程与不等式部分的中档题，涵盖了不等式组、分式方程、一元二次根与系数的关系，是中考的常考题，让学生通过再次强化练习体味该类问题的基本思路及方法. 例题数量不多，不占用课堂中的大量时间，而把大部分时间留给学生主动学习.

挑战新高，激发创造

二轮复习是在一轮系统全面复习后进行的，学生已具备一定的基础，因此题目的选取很重要. 问题要有一定的深度，但不是越难越好，太难会让学生有挫败感而降低对数学的信心，太简单则不利于能力的提高. 根据心理学规律，将问题至于“最近发展区”，让学生“跳一跳，够得到”，这样不仅能让学生从解题中找到自信，增加进一步探究的欲望，而且也能从自己不会解决的问题中发现自己知识的欠缺，寻找错误根源，及时进行查漏补缺.

如专题“数与式”是初中数学的基础，是学生认识代数的“领路人”，这部分内容虽以计算为主，但在二轮复习中则不能以简单的计算题作为例题来讲，而要采用综合题加上变式训练来提高学生的能力.

例4  已知m+n=5，mn=3，求m²+n²的值.

变式思考1：设m>n>0，m²+n²，求（m+n）/（m-n）的值.

变式思考2：由变式1的启发，请你再设计一道类似的问题，并解答.

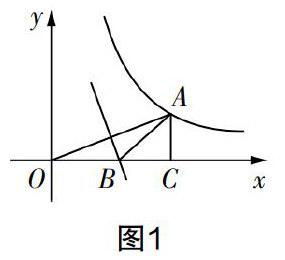
变式思考3：如图1，点A在反比例函数y=6/x（x>0）的图像上，且OA=4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B. 求△ABC的周长.

通过对一题多变及综合性问题的分析，一方面可以让学生知道前后知识的内在联系，体会数学知识的连贯性;另一方面，这个问题的难度能给学生提供探究的平台，拥有提高的空间. 在二轮复习中，可以适当增加开放型和半开放型问题的比例，让学生不但拥有解决问题的能力，而且逐渐形成提出问题的能力，激发学生的创造性.

总结规律，提炼方法

总结数学规律、归纳数学思想、提炼解题方法是二轮复习的主要目标. 只有不断总结，才能发现数学中的规律;只有体会到数学思想在解题中的渗透，才能形成数学意识;只有领会到数学方法的使用，才能让成绩有稳定和持久的提高.

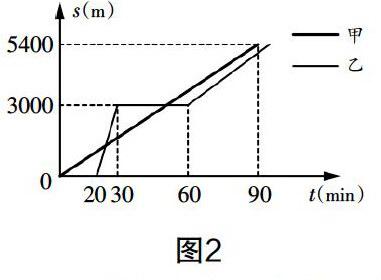
例如专题“图表信息类问题”中，选用如下例题：某景区的三个景点A，B，C在同一直线上，甲、乙两名游客分别从景点A出发，甲步行到景点C，乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C. 甲、乙两人离开景点A后的路程s（m）关于时间t（min）的函数图像如图2所示.

（1）乙出发多长时间以后与甲相遇？

（2）要使甲到达景点C时，乙与C的路程不超过400 m，则乙从景点B步行到景点C的速度至少为多少？（结果精确到0.1 m/min）

此问题为一次函数的应用问题，（1）可以用待定系数法求出一次函数的解析式，进而利用两函数值相等时即为相遇，求出时间即可. （2）根据题意得出两人相距400米，乙需要步行的距离为：5400-3000-400=2000（米），需要的时间为30分钟，进而得出答案. 建立函数思想解决实际问题是求解图表信息类问题的基本思路，在例题的讲解中让学生感知函数模型的建立，总结图表类问题的基本思路：看图→解图→建模→求解，从而更好地理解模型思想的渗透.

任何一个数学专题的复习，教师都应将关注点置于规律的总结和方法的提炼上，这样才能发挥专题复习的作用，让学生从一道题的解法中领悟一类题的解法.

突出重点，提升能力

专题复习阶段是训练学生们综合运用所学知识，形成稳固的知识体系以适应中考的阶段，提升数学能力是这一阶段的复习目标. 在这一阶段的复习中，教师尤其不能剥夺学生的自主能力，尽量让学生自己讲、自己悟. 如在“几何最值问题的常见题型和解题方法”中，选取如下四个问题作为例题：

例5  如图3，长方体的底面边长分别为2 cm和4 cm，高为5 cm. 若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为（      ）

A. 13 cm      B. 12 cm

C. 10 cm      D. 8 cm

例7  如图5，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC，CD上分别找一点M，N，当△AMN周长最小时，则∠AMN+∠ANM的度数为（      ）

A. 130°      B. 120°      C. 110°     D. 100°

【变式】 如果∠BAD=110°，其他条件不变，则∠AMN+∠ANM=______.

例8  如图6，正方形ABCD的边长为1 cm，M，N分别是BC，CD上两个动点，且始终保持AM⊥MN，当BM=______cm时，四边形ABCN的面积最大，最大面积为______cm2.

【变式】  条件不变，求△AND的最大面积和最小面积.

这四个例题分别代表了线段长度最值、线段之和最值、周长最值、面积最值这四种具有代表性的类型，是考纲中规定的重要考点. 在讲解时，凸显重点，让学生领会两点之间线段最短求最值、垂直线段最短求最值、用轴对称求最值、二次函数求最值的基本思想.

二轮复习一定要有针对性，突出重点、突破难点，让学生通过最实用的训练与探究，使自己的能力得到提高.

数学是思维的体操，解决数学问题能让思维得到锻炼，二轮复习目的是让学生将前后知识相联系，学会每类题型的思路，能对问题进行举一反三、触类旁通，通过专题的训练达到知识的整合. 二轮复习的效率不仅影响学生的中考成绩，而且还影响学生今后學习和生活中的思维方式，所以教师应不断探索、不断改进，力求更大地发挥二轮复习的时效性，关注复习的效率，提升学生的能力，不仅能让学生受益，也能促进自身的专业成长.