学材再建构 课堂再升级

朱爱平

[摘  要] 教学中应遵循“学法三结合，学材再建构，学程重生成”的规则. 单元教学是在理解的基础上重组教材，从“教教材”到“用教材教”，同时在过程中渗透数学思想和方法，得到学习数学的通法.

[关键词] 学材再建构;学情;自主建构

在2018年4月15号到4月17号为期三天的第三届李庾南实验学校数学优课评比活动中，涉及三节学材建构的课题，初赛课题“24.2.1  点和圆的位置关系”和决赛课题“26.1.1  反比例函数”“28.1锐角三角函数”二选一. 在决赛中笔者抽到了第二节课，比赛的要求是充分体现以学生为主体，在师生合作中学会学习，学会自主建构发展的核心理念，遵循“学法三结合，学材再建构，学程重生成”的规则，着重推行单元教学，从“教教材”到“用教材教”，同时在过程中渗透数学思想和方法，得到学习数学的通法.

现以“28.1锐角三角函数”为例，给出课堂实录，请同行一起研讨.

问题引领，平行迁移

问题是思维的导火线，课堂教学过程中，教师采用问题的形式启发学生的思考，引领学生的思维方向，让学生在问题的引领下学会思考、学会对比、学会迁移、学会建构. 这种学会是自发的、感悟的、渐进的，是学生学习能力真正提升的关键所在. 比如本节课，在第一环节就采用如下问题.

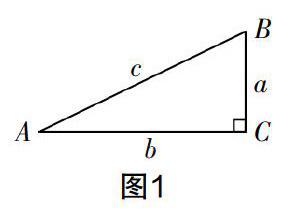
师：请同学看图1，今天老师给你们带来了什么图形？

生1：直角三角形.

老师板书：在Rt△ABC中，∠C=90°.

师：这个直角三角形除了∠C=90°，还有哪些结论呢？

生2：∠A+∠B=90°，a²+b²=c².

师：我们学习了直角三角形锐角的关系和边的关系，那么锐角和边又有什么关系呢？这节课开始我们就来学习直角三角形锐角和边的关系（板书章节标题“28.1锐角三角函数”）.

自主生成，形成概念

自主生成，水到渠成地形成概念才是真正的自主架构. 在教师问题的启发下，学生的思维层层递进，概念也渐渐明朗，最终自发地建构新的概念，呈现新的认知.

师：锐角以∠A为研究对象，AB为斜边，BC，AC为直角边，为了区分，我们把BC叫作∠A的对边，AC叫作∠A的邻边. （如图2）

教师拿一个大的三角板和学生用的三角板（都含有30°）提问：请同学们观察一下这两个三角形有什么相同点，又有什么不同点.

生1：它们的角度相同，但边长不等.

师：角度相同，但是边长不等，在邊长不等的表面现象下，是否隐藏着不变的量呢？

（生疑惑中）

师：请问在大的三角形中，这个锐角是多少度？你会联想到什么？

生异口同声：30°，30°所对的直角边是斜边的一半.

师：那么你们发现了什么呢？

生2：30°角的对边与斜边的比值是确定的.

（教师板书搭出表格的框架）

各个小组接二连三地发现了一些边的比值是确定的，老师都给予了肯定.

师：∠A的对边、邻边和斜边，两两组合有几种？那么它们的比值有几种？它们之间的关系又是什么？

生3：∠A的对边与斜边;∠A的邻边与斜边，∠A的对边与∠A的邻边，一共有三种组合，比值的顺序不同，每种组合有两种比值，它们互为倒数，一共是六个比值.

（教师进一步完善表格的框架和数值）

生齐声回答：有！

（课堂进入了小高潮）

师：我们一起运用几何画板实验验证一下，是否∠A取定一般的锐角，这些比值还是唯一确定的.

师：如图3，此时的∠A为54.93°，我改变三角形的大小，请同学观察图旁的两组数据，你发现了什么？

生6：我发现当∠A取定为54.93°，三边的长度可以变化，但是这些边的比值是不变的.

师：如图4，此时∠A为66.28°，观察得出结论.

生7：边长变，而三组边的比值唯一确定.

师：当我们学习相似以后，还可以很方便地通过推理证明得出猜想.

生齐答：函数.

师：这些边的比都是∠A的函数，我们把这些函数叫作∠A的锐角三角函数.

（搭出板书框架）

教师给出了正弦、余弦、正切的定义和符号表示并进行了表格的完善.

师生一起朗读了正弦、余弦、正切的定义和符号表示形式，强调记忆方法：正即正对即对边，勾股弦中弦记为斜边.

巩固概念，生成新知

温故而知新、知新而启思、启思而启智，在数学课堂中，及时巩固概念是必需的，并且在巩固概念的基础上再次启发思考，再次自主建构新知. 本节课中笔者进行了如下设计.

请思考问题1：如图5，求直角三角形两个锐角的正弦值、余弦值和正切值.

sinA=________;sinB=________;

cosA=________;cosB=________;

tanA=________;tanB=________.

师提问：（1）观察这里的六个数值，你有什么发现？（2）能把你的发现用语言概括一下吗？

sinA=________;sinB=________;

cosA=________;cosB=________;

tanA=________;tanB= ________.

师：通过这个问题我们就可以推理证明出猜想的正确性，由此我们把发现的结论叫作锐角三角函数的性质.

巩固旧知，再生新知

基于训练中存在的不足和暴露出来的问题进行变式与再训练是非常有效的. 这种训练目标明确、针对性强，并带着启发新知、促进再生长的问题进行突破，达到由此及彼、举一反三的效果.

师：如表2，老师不小心擦掉了特殊角三角函数表中的一些数据，请同学帮我补上数据，并说出你的方法.

生1：我利用了定义来解决.

生2：我运用了刚才发现的同角三角函数值的性质和互余两角三角函数值的关系来填写的.

师：孩子们表现得都很好，一位同学抓住了定义，定义是一切性质的根源，一位同学灵活运用了发现的结论，高效完成数据的填写，为他们点赞.

师：研究函数都会研究它的增减性，你能借助表格得出正弦函数、余弦函数和正切函数的增减性吗？

生3：表格中∠A的度数从30°到45°再到60°，角度在依次增大，正弦、余弦、正切在依次增大、减小、增大，所以我猜测正弦为递增函数、余弦为递减函数、正切为递增函数.

师：很好，这位同学掌握了我们学习数学的一般方法，通过观察、发现猜想出结论，那么我们也来用几何画板验证一下猜想的结论，如图7～图9.

师：由此我们发现刚才的猜想是正确的，当然以后学习了三角函数的图像就能直观地反映函数的增减性了.

师：老师有个问题想问一下大家，正弦随着角度的增大而增大，它会增大到什么程度呢？

课堂再次进入了高潮，大家都有了困惑，也很想知道这个问题的答案. 老师引导学生再次回归定义的根源，先独立思考，再小组交流三个函数值的范围.

师：合作的力量就是大，该组的分析非常全面到位.

反思总结，质疑提升

在学习中进行总结与反思、质疑与反问是一种学习习惯，更是一种学习能力. 在课堂教学过程中，教师要引导学生善于自我总结、自我反思、自我归纳，而教师则是通过提炼提纲挈领的问题来帮助学生反思总结，不仅协助学生总结，也教会学生注重总结的知识性、方法性、框架性，提升总结的价值.

提出的问题如下：

1. 这节课我们学习了哪些知识？你是如何理解∠A的正弦、余弦、正切都是∠A的锐角函数的？

2. 在学习探究的过程中，我们有了哪些思想方法上的收获？

3. 猜一猜我们还将学习锐角三角函数的哪些知识？

师生共同总结：

1. 本节课学习了三角函数中的正、余弦和正切的定义、自变量范围、部分性质;随着∠A的变化，它的正弦、余弦和正切都在变化，当∠A取定一个锐角的度数，正弦、余弦和正切都有唯一确定的值与之对应，这些研究的前提都是在直角三角形中.

2. 对于直角三角形的锐角和它的边之间的关系，我们经历了特殊到一般再到特殊的过程;再从特殊的数值进行观察、发现、猜想、验证，经历了研究数学问题的一般方法.

3. 还将会研究三角函数的图像和应用.

分层练习，自我提高

基于学生的客观差异开展分层练习，不仅是学生发展的需要，也是教材价值达成的最佳呈现形式. 在本节课的教学过程中，基于笔者所带班级的实际情况，设计了如下的分层练习，能从知识与技能、方法与思想上满足所有学生训练和提升的需要，能较好地促进学生对本节内容的理解与应用，具体分成两个板块，一个是必做，一个是选做.

必做题：

1. Rt△DEF中，∠F=90°，EF=5，DE=13，出∠D 和∠E的正弦、余弦和正切.

2.在△ABC中，∠C=90°，sinA=1/2，求cosA、tanA.

3.已知∠A+∠B=90°，請把（90°-∠A）的三角函数写成∠B的三角函数.

选做题：

本文板书设计如下（如图11）.

学情是让初二的同学学习初三的内容，在学生没有学习相似的基础上学习锐角三角函数正弦、余弦和正切的概念. 单元教学考虑到容量比较大，设想了进行学材再建构，过程中知识的生成侧重问题引导，学生自主、自动、自由地获得发展. 每个知识的获得顺畅自然，但过程中缺少了给学生消化的时间，在单元教学的实践中还不成熟，笔者也在自我反思和改进，同时期待更多的同行专家给予指点和斧正.