整体法，教学简单数学

胡静

[摘 要] 整体法是一种重要的数学思想，在高中教学阶段的应用及其广泛，是解决复杂数学题的不二法宝.为了提高高中生整体的数学素养，养成良好的解题习惯，教师要学会在平常教学中向学生灌输整体法的使用思路，为学生的学习提供便利.

[关键词] 整体思想；高中数学；简单教学

在当今环境下，课程改革活动正在如火如荼地进行，新型的课堂教学模式正在席卷高中数学课堂. 作为数学教师也要适应时代的步伐，争做改革的领跑者，摒弃以往腐旧的教学模式，开创对学生有益的教学方式，全面提升学生的整体数学素养. 整体法作为一种便捷的解题工具，是教师实现轻松教学、简单教学的秘密武器，只要教师能够应用得当，数学课堂一定会精彩纷呈. 笔者本人具有多年高中数学教学经验，对如何在课堂教学中以及习题训练中渗透整体法的使用具有一定的研究与探索，下面简要介绍几点经验，不足之处，敬请斧正.

整体代入，绝处逢生

整体代入是整体法最直接、最明显的表现方式，就是将若干个式子组合在一起看作一个整体，通过直接或者间接的方法代入另一个式子当中，使解题过程变得简单，避免烦琐的计算过程，于绝处逢生，给学生的解题带来希望.

整体代入在高中的各个阶段都会应用，就连最简单的长方体教学中也会出现这种方法的使用. 教师在平时授课中，为了让学生更快、更好地吸收知识、理解知识，一定要将教学内容变得简单，利用整体法就是不错的选择. 例如，当我们学完长方体的相关知识后，笔者都会向学生布置这样的习题：已知长方体的全面积是11，十二条棱长总和为24，那么请分析这个长方体的一条对角线的长度为多少. 面对这道题，一般的解题思路是先假设长方体的长、宽、高分别为a，b，c，根据已知条件分别求出a，b，c的值，然后再依据对角线长的公式即d=进行计算. 但是我们明显会发现根据已知条件无法求出a，b，c的值，因此我们就需要考虑其他的方法. 我们可以先将对角线长的公式进行变形，然后再考虑接下来怎样计算，d==，根据这个式子，我们可以发现只需要求出a+b+c和ab+bc+ca即可. 再根据已知条件列出下列式子：2（ab+bc+ca）=11，4（a+b+c）=24，这样我们就可以分别求出两个需要的式子的值，代入表达式中可以得出d=5. 在这道题的解决过程中，我们就采用了整体代入的思想，因而才使得题目得以解决. 如果仅仅采用正常的思路进行求解，这道题目也是无法计算的，由此可见整体代入的重要性.

整体代入在很多数学知识中都可以应用，都能够起到简化题目的作用. 教师要在平常教学中不断地去探索、发现更多的整体代入例题，并及时地与学生进行分享，用以扩宽学生的视野，增加学生的解题经验.

整体换元，柳暗花明

整体法是高中的重点知识，有很多问题只能够通过整体法才能够解决，因此教师要提示学生提高警惕，将整体法的各种应用都熟记于心，这样在应用时才能够信手拈来，避免出现卡在读题阶段不知如何下手的尴尬局面.

整体换元属于研究新元性质方面的知识，在多项式部分应用较多，它能够将题目进行转化，变得简单易解.当教师在教学多项式方面知识时，一定要确保学生能够独立应用整体换元的思想解决实际问题，因为在高考中这个考点也会频繁出现. 下面以一道简单的例题为例，介绍整体换元使用的妙处. 请计算（a1+a2+…+an-1）（a2+a3+…+an-1+an）-（a2+a3+…+an-1）（a1+a2+…an）的值. 面对多项式与多项式乘积的题目，一般的思路是将括号打开，逐一进行计算，但是本题给出的并不是具体数字，而且数字较多，这种方法根本不适合用来解这道题. 这时我们就需要向整体换元法求助，将题目转化成简单的形式，能够一眼看出解题思路即可. 整体法重要的思想就是要求大同存小异，进行整体变换，题目就会变得简单. 设a2+a3+…+an-1=x，则原式=（a1+x）（x+an）-x（a1+x+an），注意将式子打开并进行化简计算，就会得出原式=a1an，由此就可以得出正确答案.根据解题过程可知，虽然我们假设a2+a3+…+an-1=x，但是在后面的计算中可以直接将x消去，并不影响整道题目的解题程序. 在此也能够看出整体换元的妙处，将复杂的式子变得简单，使式子变换到学生可以接受的程度，之后再进行化简计算就会显得异常简单了.

多项式的计算是高中的重点知识，教师一定要想方设法帮助学生突破这个教学难点，将整体换元法把握透彻，让学生有信心去面对复杂的高考，在考试中平稳地拿下高分.

整体变形，水到渠成

整体变形既是整体法的一种应用实例，又是思维转换的具体表现，需要学生拥有独特的眼光，发现问题的本质所在.只有抓住问题的主要矛盾，才能够想到合适的变形方法，将问题转化为熟悉的内容，加快解题速度.

在使用整体变形这种解题方法时，学生首先要对题目有一个完整的认识，找到问题的关键才能够水到渠成地解决问题. 当我们在学习数列知识时，教师都会向学生讲授整体变形的应用实例，提高学生对数列的认识. 其实，只有在讲解数列知识时才是传授整体法的最佳时机，整体法是解决数列问题的法宝.数列知识较强的学生，整体法的应用都会十分熟练. 例如，学生在习题训练中，都会遇到这样的题目：已知数列{an}的通项公式为an=（2n-1）xn（x≠1），求出此数列的前n项和Sn. 解决此题时，一般思路是先求出数列的前几项，之后再决定采用何种方式解题. 利用通项公式可以求出a1=x，a2=3x2，a3=5x3……观察这前几项可以发现，这个数列既不是等差数列也不是等比数列，这时在进行前n项和求解时，我们不可以根据数列的相关公式直接求出. 所以我们要采用其他的方法，先写出前n项和Sn的公式：Sn=x+3x2+5x3+…+（2n-1）xn，观察式子，我们可以将式子两边同时乘x，将式子进行整体变形，得到xSn=x2+3x3+5x4+…+（2n-1）xn+1，然后再将上面两个式子相减，就可以求出Sn. 具体计算过程比较简单，在此不再赘述. 这种解题方式，就是在原有的式子的基础上构造一个新的与题目相关的式子，二者进行恰当的运算，就可以得出Sn的值.

整体变形法开拓了一种新的解题思路，增加了学生解题的砝码，使学生能够轻松地解决数列的相关知识.

整体补形，迎刃而解

立体几何是学生进入高中以来所学习的数学知识中最需要想象力的知识模块，因此也是很多想象力匮乏的学生的学习软肋，他们无法找出图形中需要的线段或者图形，也就不能得到合适的解题方法. 整体补形能够帮助学生在立体几何的学习中搭建全新的视角，有利于学生抓住问题的重点，找到最佳解题途径.

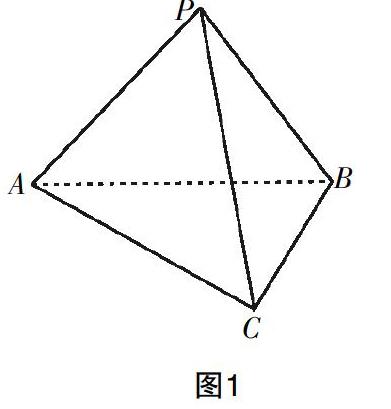
利用整体补形法解决立体几何相关问题是一个专题，教师在进行总复习时，可以抽出一定的时间进行专门的知识总结以及扩展，让学生对整体补形有一个全面的把握，增多学生的解题技巧. 在专题训练中，教师要尽可能多地选择具有代表性的题目，让学生每做一道题目都会有独特的收获，能够对学生的思维模式起到促进的作用. 例如，当笔者在组织学生进行复习时，都会留下这样的题目：如图1所示，在三棱锥P-ABC中，三组对棱相等，并且PA=13，PB=14，PC=15，求出这个三棱锥的体积.

按照常规的解题思路，求解三棱锥的体积要先求出其底面积，然后再求出其高，之后再利用所学公式进行求解. 但是在这道题目中，底面积容易求出，高却不好求，因此我们就需要考虑其他方法. 在根据已知条件三组对棱相等，可以联想到长方体对面不平行的对角线也具有此性质，从而我们可以将三棱锥补成一个长方体，如图2所示，从而能够快速地解决问题. 整体的解题思路就是三棱锥P-ABC的体积等于长方体的体积减去4个三棱锥A-BCD的体积，代入相关的数据就可以轻松地求出答案.

这道题目就将三棱锥与长方体巧妙地联系到了一起，是一道不错的综合性题目，教师要为学生多多准备类似的题目进行训练.

总之，当我们在解决数学问题时，如果能够仔细观察问题，找出题目的主要矛盾，在大处着眼把握全局，合理巧妙地利用整体法进行解题，都会起到事半功倍的效果，整体提高学生的数学素养.