浅谈函数零点个数问题的解题策略

王志刚

(江苏省丰县民族中学，221700)



浅谈函数零点个数问题的解题策略

王志刚

(江苏省丰县民族中学，221700)

函数零点个数问题是高中数学中的常见问题，在各类考试中经常出现.这类问题的解决不仅涉及到基本的数学知识,还涉及到基本数学思想方法,比如化归思想,数形结合,整体代换等等.笔者根据多年的教学实践,结合着各类习题谈一下解决相关问题的常用策略.

策略1利用函数零点存在性定理

若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线，且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点，这就是函数零点的存在性定理.若条件中再添加“函数在区间[a,b]上是单调的”,则结论变为函数y=f(x)在区间(a,b)上有且只有一个零点.

例1函数f(x)=2x+x3-2在区间(0,1)内零点的个数是______.

解因为f(x)=2x+x3-2在(0,1)上单调递增，又因为f(0)=-1<0,f(1)=1>0，故f(0)f(1)<0.

所以f(x)在(0,1)内仅有一个零点.

策略2采用数形结合法.

作出函数的图象,函数图象与x轴交点的横坐标即为函数的零点.若不能作出函数F(x)=f(x)-g(x)的图象,可以将F(x)的零点问题转化为y=f(x)与y=g(x)的图象的公共点个数问题.

例2(2015年江苏高考题)已知函数

f(x)=|lnx|,

则方程|f(x)+g(x)|=1实根的个数为______.

分析由|f(x)+g(x)|=1，可得

g(x)=-f(x)±1.

分别作出函数的图象,即可得结论.

解由|f(x)+g(x)|=1，可得

g(x)=-f(x)±1.

g(x)与h(x)=-f(x)+1的图象如图1所示,显然两图象有两个交点;

g(x)与k(x)=-f(x)-1的图象如图2所示,两函数图象也有两个交点.

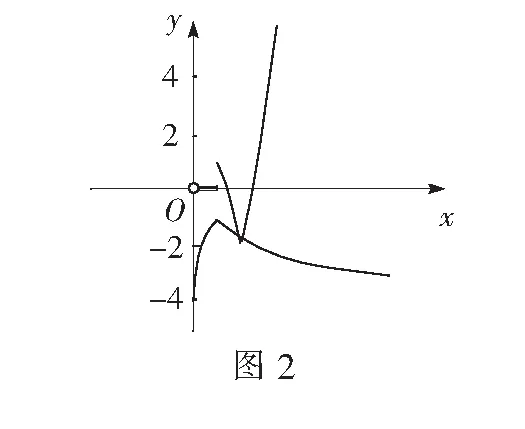
综上所述,原方程的实根个数为4.

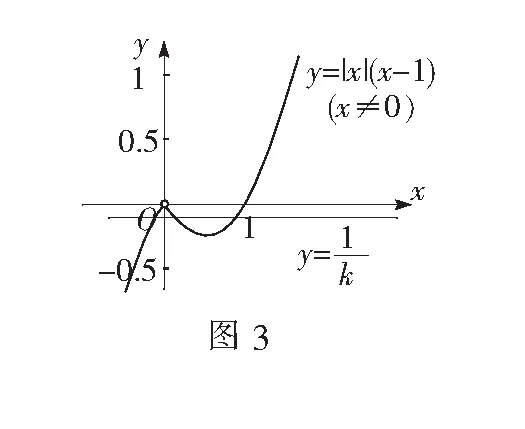
策略3运用函数的奇偶性

奇偶函数的图象具有对称性,其零点是成对出现的.在求奇偶函数在对称区间上零点的个数时,可以先研究其在x正半轴定义域内的零点个数再借助于奇偶性得出零点个数的总数.

例4若y=f(x)是定义在R上周期为2的周期函数且为偶函数.当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-log5|x|的零点个数为______.

分析函数g(x)=f(x)-log5|x|的零点个数即为f(x)-log5|x|=0根的个数,亦为函数y=f(x)与函数y=log5|x|图象交点的个数.显然,它们均为偶函数,故只需分析它们在x>0时图象交点的个数,再根据对称性求出总数.

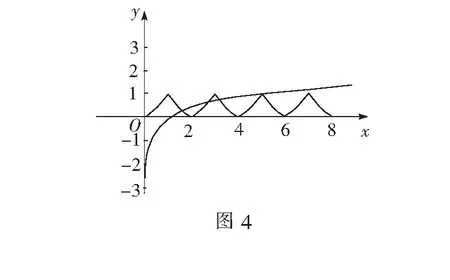
解函数y=f(x)与y=log5|x|在x>0时的图象如图4所示.它们的交点有4个.由对称性可知,它们在x<0时也有4个交点.故两函数图象共有8个交点,从而原函数有8个零点.

策略4利用换元法

换元法是数学中整体思想的体现,是适用面较广的方法之一,灵活熟练地使用该法往往可以降低问题的难度,为快速正确地解决问题打下坚实的基础.在函数零点个数的问题中,也能起到同样的效果.

例5(2013年安徽高考题)已知,函数f(x)=x3+ax2+bx+c有两个极值点x1和x2.若f(x1)=x1,则关于x的方程3[f(x)]2+2af(x)+b=0的不同实根的个数为______.

分析注意到方程

3[f(x)]2+2af(x)+b=0

(*)

就是把f(x)代入方程f′(x)=0得到的.

利用换元法设f(x)=t,于是方程(*)可化为

3t2+2at+b=0.

由题意可知,该方程的根为t=x1,t=x2，即f(x)=x1,f(x)=x2.在同一平面直角坐标系内,画出函数y=f(x),y=x1,y=x2的草图即可得出结果.

解f′(x)=3x2+2ax+b.令t=f(x)则原方程变化为f′(t)=0.由条件函数有两个极值点x1和x2，知f′(t)=0有两个实根t=x1和t=x2,故两方程f(x)=x1,f(x)=x2的根就是原方程的根.

不妨设x1

综上可知,解决函数零点个数问题的方法多种多样.在今后的学习中,我们除了要加强数学基础知识的学习之外,还要善于归纳,总结,反思,才能根据问题的特点,选择最合适的方法,才能对数学知识有更加深入的认识,才能站在更高的地方重新观察问题,思考问题,从而把握问题的关键,在各种考试中避免不必要的失误,获得理想的成绩.

(B) (-∞,2)

解析令t=3x(t>1),则由已知得函数f(t)=t2-mt+m+1的图象在t∈(1,+∞)上，且恒在横轴的上方,则对于方程f(t)=0有Δ=(-m)2-4(m+1)<0.