巧用“轨迹” 优化解题

周玉琴

(江苏省常州市第一中学，213003)



○解题研究○

巧用“轨迹”优化解题

周玉琴

(江苏省常州市第一中学，213003)

当高三进入二轮复习时,学生的知识框架已经建构好，各种解题的方法也都接触过．平时教师在讲解时,会一题多解,也会多题一解．在笔者连续四年的高三数学教学中,每一届学生都会提出同一个问题:老师,我在做题时,怎样才能很快决定用最好的方法．我总是鼓励他们:平时要多尝试,多总结归纳,用心去”捂”,方能达到“出招”必胜!

话虽然是这么说的,但是学生的”招数”还是源于老师的指导．在二轮复习中,我一直注重引导学生掌握基本方法的同时进行解题的优化．其实优化方法都源于最基本的概念．下面是笔者在进行微专题复习时利用“轨迹”求最值问题或是范围问题的几个案例．

一、几个“轨迹”

(1) 点的轨迹是直线(线段等)；

(2) 点的轨迹是圆(圆面,圆内外等)；

(3) 点的轨迹是椭圆；

(4) 点的轨迹是双曲线；

(5) 点的轨迹是抛物线.

二、寻求“轨迹”

1.题目中有明显的“轨迹”

案例1在一轮复习三角时,给出了下面的一个例题；

刚接触到这个问题时,学生往往利用余弦定理来建立函数模型(略),计算比较复杂．介绍了圆的第二定义(阿波罗尼斯圆)后,解决此题显然手到擒来．

解建立直角坐标系，如图1，A(-1,0)，B(1,0).设C(x,y)，

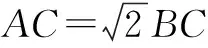
(x+1)2+y2=2[(x-1)2+y2]，

即点C的轨迹方程为

(x-3)2+y2=8(y≠0).

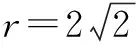
因为此题出现在三角函数复习期间,学生的思维角度多数是定在运用正余弦定理．用此方法解决问题的学生显然是跳出了知识的框框,也是让其他学生眼睛一亮的地方．在复习了圆锥曲线后,学生在解题时灵活运用定义的意识强多了．

例如，如图2,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,∆CPD的面积为f(x)，则f(x)的最大值为______;

在解决此题时,大部分学生能灵活应用椭圆的定义来解决．

2. 题设中隐藏的“轨迹”

有的题目，轨迹“隐藏”其中,只有拿起数学思想揭开其中面纱,才能到达成功的彼岸.

案例2下面是教学中的 一个例题：

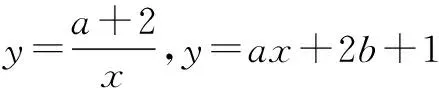
当问题分析到这儿的时候,多数学生觉得做下去如果要进行讨论的话会很繁琐．

师:既然觉得现有的方法不可操作,那看看能否有另外的途径?

下面进行小组讨论．在讨论中有学生注意到目标函数的几何意义．

把a,b看成主元，x为参数，其方程表示为一条直线，于是方程a(x2-1)+2bx+x-2=0在[3,4]有解等价于将方程a(x2-1)+2bx+x-2=0看成关于a，b的一条直线.于是a2+b2的几何意义就是直线上一点(a,b)与原点(0，0)的距离的平方，则a2+b2≥d2，其中d是原点到该直线的距离.

3.利用“双轨迹”化归

若一动点同时在两条轨迹上运动,就可以把问题转化为两条轨迹的关系．如已知点A(0,2)，B(0,1),D(t,0)(t>0),M为线段AD上的动点,若AM≤2BM恒成立，则正整数t的最小值是______.

学生显然会去设点M(x,y)，由AM≤2BM得到点M的轨迹C，而点M又在线段AD上，所以就转化为线段AD与轨迹C的关系，即线段和轨迹C相离.以下这道试题正是这种”双轨迹”的问题.

案例3(2016年江苏高考题)如图3,在平面直角坐标系中,已知以M为圆心的圆M：x2+y2-12x-14y+60=0及其上一点A(2，4).

(1) 设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;

(2) 设平行于OA的直线l与圆M相交于B，C两点,且BC=OA,求直线l的方程;

解析(1)(2)略.

又(x2-6)2+(y2-7)2=25,得

圆G：(x1-t-4)2+(y1-3)2=25.

又(x1-6)2+(y1-7)2=25,

所以点P既在圆M上又在圆G上，从而说明圆M和圆G有公共点，即

0≤GM≤10,

正是有了扎实的“轨迹”思想的渗透,学生来解决这个问题时就会容易解决．