高中数学信息情境题解题要领

林惠贤

(广东省佛山市南海区大沥高级中学，528231)



高中数学信息情境题解题要领

林惠贤

(广东省佛山市南海区大沥高级中学，528231)

纵观近几年高考数学试卷,每年的高考试题中都有一道或者两道信息情境题作为创新的题目,成为当年高考试题的亮点．新颖的题型对于考生来说,是有一定的难度,因为考生从来没有见过,从认识到理解、到分析、到解决,需要一个过程,大多数考生都望而生畏,得分率并不理想．

事实上,高考数学中出现的信息情境题并非“高不可攀”.所运用到的知识一般不会很复杂,它侧重于考查学生知识的迁移能力——会利用已有的知识和经验发现和提出有一定价值的信息、运用有关的数学思想和方法,对问题进行探究,寻求数学对象的规律与联系,从而解决问题．下面,笔者结合一些具体的实例,谈谈这类问题的一些解决方法．

一、消除恐惧,调整好心态．

例1(2006年广东高考题)对于任意的两个实数对(a,b)和(c,d),规定:(a,b)=(c,d)当且仅当a=c,b=d;运算“⊗”为:(a,b)⊗(c,d)=(ac-bd,bc+ad);运算“⨁”为:(a,b)⨁(c,d)=(a+c,b+d).设p,q∈R,若(1,2)⊗(p,q)=(5,0),则(1,2)⨁(p,q)=()

(A)(4,0) (B)(2,0)

(C)(0,2) (D)(0,-4)

例2(2007年广东高考题)设S是至少含有两个元素的集合，在S上定义了一个二元运算“*”(即对任意的a,b∈S对于有序元素对(a,b)在S中有唯一确定的元素a*b与之对应).若对于a,b∈S，有a*(b*a)=b则对任意的a,b∈S下列等式中不恒成立的是()

(A)(a*b)*a=a

(B)[a*(b*a)]*(a*b)=a

(C)(b*b)*b=b

(D)(a*b)*[b*(a*b)]=b

例3(2010年广东高考题)设A(x1,y1),B(x2,y2)是平面直角坐标系xOy上的两点,现定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)=|x2-x1|+|y2-y1|.对于平面xOy上给定的不同的两点A(x1,y1),B(x2,y2),若点C(x,y)是平面xOy上的点,试证明：

ρ(A,C)+ρ(C,B)≥ρ(A,B).

分析不少同学一接触这类题目,第一反应就是觉得害怕,心里不踏实,看到一些教科书上从没出现过的陌生的名词、符号、定义,缺少战胜的信心和勇气,造成了解题的一大心理障碍．其实,这三道题并不困难,前两题只要理解了新定义的运算符号“⨁”和“*”的本质含义,就可以轻易选出正确答案分别是D、A．至于例3,考生在明确新定义后,直接由绝对值不等式可以证明：

ρ(A,C)+ρ(C,B)

=|x-x1|+|x2-x|

+|y-y1|+|y2-y|

≥|(x-x1)+(x2-x)|

+|(y-y1)+(y2-y)|

=|x2-x1|+|y2-y1|

=ρ(A,B)，

当且仅当(x-x1)(x2-x)≥0且(y-y1)·(y2-y)≥0时等号成立．

命题得证．

所以,树立良好的心态,是成功的第一步．

二、细致审题,善于把握有用信息,善于对知识进行迁移或类比

信息情境题一般都是多维的、非常规的知识综合,有时需要知识与方法的迁移、远距离的知识交汇,某些问题还在背景、方法上实现迁移．若按设计背景的性质来分,主要有以下三大类型:

1.以生活世界为背景

这类题目主要提供了数学世界的现实原型与应用空间,具有直观性、真实性、经验性、朴实性、实用性等特点．贴近生活、贴近学生实际、贴近问题的实际,把应用问题生活化．

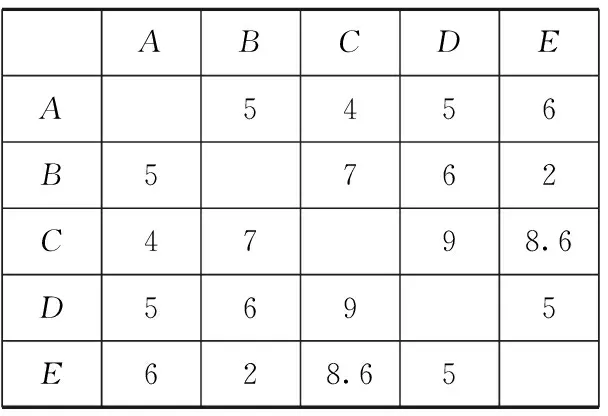
例4(2009年广东高考题)广州2010年亚运会火炬传递在A,B,C,D,E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表．若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短路线距离是()

(A)20.6(B)21(C)22(D)23

ABCDEA5456B5762C4798.6D5695E628.65

分析这是一条以时事热点“广州亚运”为背景的信息情境题.由题意知,所有可能路线有6种:①A→B→C→D→E,②A→B→D→C→E,③A→C→B→D→E,④A→C→D→B→E,⑤A→D→B→C→E,⑥A→D→C→B→E, 其中, 路线③A→C→B→D→E的距离最短, 最短路线距离等于4+9+6+2=21,故选B.

例5(2007年广东高考题)图1是某汽车维修公司的维修点环形分布图.公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为()

(A)18(B)17(C)16(D)15

分析本题的关键信息是“ 调整只能在相邻维修点之间进行”.因此,可设A调出x件给D(0≤x≤10),调出了10-x件给B,B调出了5+10-x=15-x件给C,C调出了15-x-4=11-x件给D,此时调动总次数N=x+(10-x)+(15-x)+(11-x)=36-2x,当且仅当x=10时,N取得最小值16,故应选C．

2.以高等数学知识为背景

近几年高考数学加强了中学数学与高等数学的衔接,将高等数学中的基础知识直接引用,以信息情境题的形式考查,如函数凸凹性、不动点问题、中值定理等知识．

例6(2002年上海春季高考题)对于函数f(x),若存在x0∈R,使f(x0)=x0,则称x0是f(x)的一个不动点,已知函数

f(x)=ax2+(b+1)x+(b-1)(a≠0).

(1)当a=1,b=-2时,求函数f(x)的不动点;

(2)对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;

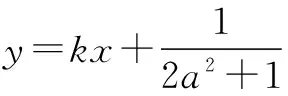
分析这是一道以“函数不动点”为载体的高考试题.题目直接给出“函数不动点”的定义,旨在考查学生对新信息的领悟和理解能力.读懂题意后,前两道小题就不难解决,实质考查的是高中生所熟悉的二次函数与方程的相关知识．对比之下,第3小题则有一定的难度,属于能力创新题,考查学生的综合数学能力．

解(1)因为f(x)=x2-x-3,x0是f(x)的不动点,则

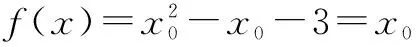
(2)∵函数f(x)恒有两个相异的不动点,∴f(x)-x=ax2+bx+(b-1)=0恒有两个不等的实根,Δ=b2-4a(b-1)=b2-4ab+4a>0对b∈R恒成立,∴(4a)2-16a<0,得a的取值范围为(0,1).

(3)由ax2+bx+(b-1)=0得

设A,B中点为E,则E的横坐标为

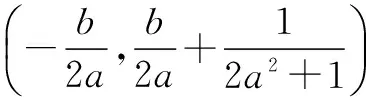
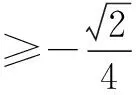
例7(第二届“南方杯”数学竞赛题)设an是以-1为首项,以7为公差的等差数列的第n项,bn是该等差数列的第n2项,定义Δbn=bn+1-bn({Δbn}叫做数列{bn}的“一阶差分”),则Δbn与an+1之间的关系是Δbn=x·an+1+y(x、y是常数),且x+y等于()

(A)11(B) 12(C) 13(D) 14

分析“一阶差分”看似高等数学的内容,实际上只是作为一个背景材料而已,只要学生能沉着冷静地细心分析,把握题目中的有用信息,并将其翻译成数学关系,不难得到

an=7n-8,bn=7n2-8,

所以进一步由已知

Δbn=bn+1-bn

得到Δbn=bn+1-bn

=7(n+1)2-8-(7n2-8)

=14n+7,

另一方面Δbn=x·an+1+y=7xn-x+y,

所以7x=14,-x+y=7,即x=2,y=9.

故选A．

3.以科学技术问题为背景

如下面两个例子中的“信息量传递”问题和信息安全上的“加密与解密”问题．

例8(2001年全国高考题)如图2,小圆圈表示网络的结点,结点之间的连线表承它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为()

(A)26(B)24(C)20(D)19

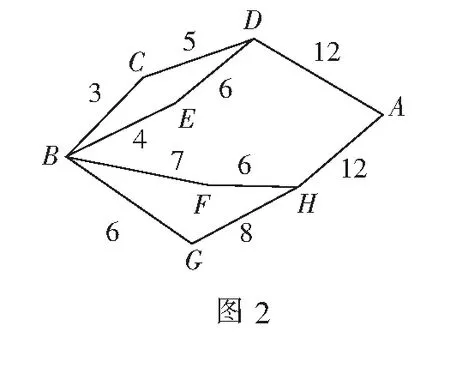
分析解决这道题的关键是读懂题意,并能从图中提取有用的数据信息．传递的路线只有4条，每条路经允许的信息量应该是一条途径3段中的最小值,所以最大信息量为3+4+6+6=19,选D.

例9(2006年陕西高考题)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为()(A)7,6,1,4(B)6,4,1,7

(C)4,6,1,7(D)1,6,4,7

分析这是一道以信息科学为背景的题目,情境对大多数学生来说都应该比较陌生,但只要理解好题目提供的有用信息——加密和解密的规则(或者说是对应关系)构造出a+2b=14,2b+c=9,2c+3d=23,4d=28组成方程组并求解,则可以很快选出正确答案C．

总之,无论是哪种类型的信息情境题,关键是要学会提取有用信息,有一定的自主学习能力和知识迁移能力．

三、适当地开阔视野,拓展课外知识面

信息情境题的背景设计空间十分广泛,为了尽量减少陌生感对解题带来了困扰,平时可以进行适当的课外阅读,加强提取有用信息的能力,多了解一些实际生活中的数学知识和现象,提高数学的应用意识．