“螺旋式提升”观点下的向量教学

徐德均

(江苏省南通中学，226001)



“螺旋式提升”观点下的向量教学

徐德均

(江苏省南通中学，226001)

课程“模块化”,可以使得同一知识在不同模块中多次出现,呈现“螺旋式提升”.即学生在学习这些知识时,要跟随学生知识的积累程度和学习能力大小,从知识的深度和广度上不断加强提高,从而在体会知识的联系和内在关联上不断加深提升,达到认知度螺旋提升,知识逐步形成、理解和应用.

向量是既有大小又有方向的量,它同时具备代数(大小)与几何(方向)两大属性,是近代数学最重要和最基本的概念之一,是高中数学教学过程中的主要概念之一,也是沟通几何、代数、三角等内容的桥梁,具有丰富的实际背景和广泛的应用.它在高中数学课程不同的模块中多次呈现,符合现行课程的“模块化”,也符合所倡导的“螺旋式提升”的教学思想.本文从高中学段中向量的教学内容、目标、要求、关注与应用等五个方面就其“螺旋式提升”,作简单梳理与归纳小结,以期得到广大同行的指导.

一、教学内容由基础到本质的“螺旋式”生成

必修4第1章“任意角的三角函数”中,呈现了向量的基本模型:有向线段与有向线段的数量.规定了方向(即规定了起点和终点)的线段称为有向线段,有向线段的长度添上正号(正方向)或负号(负方向)后所得的数叫做有向线段的数量;指出有向线段是向量几何表示,有向线段的长度就是向量的大小(长度或模).有向线段与有向线段的数量是向量的基本内容.

必修4第2章“平面向量”中,从现实生活中如位移、速度、加速度、力等量归纳定义向量及表示,并从向量的大小和方向属性定义了零向量、单位向量、平行向量(共线向量)、相等向量等特殊向量;定义了向量的加法、减法、数乘等线性运算及其运算法则和几何意义;介绍了平面向量基本定理、平面向量的坐标运算;介绍了向量的数量积与数量积的运算律;介绍了向量在物理、平面几何等应用.在有向线段与有向线段的数量知识基础上全面规范定义了有关向量的基本概念与基本运算,是一种合情的知识生成.

必修4第3章“两角和与差的三角函数”中,应用平面向量的坐标表示和数量积公式,推导两角差的余弦公式,是全面定义向量等知识后的一种合理的知识生成.

选修2-1第3章“空间向量与立体几何”中,将平面向量推广到空间向量,介绍了空间共线向量定理、共面向量定理、空间向量的基本定理、空间向量的坐标表示、空间向量的数量积等及其运算;定义了直线的方向向量与平面的法向量、介绍了空间线面关系的判定、空间的角与距离的计算等应用.这是一种合情合理的推广,并且在推广的基础上进行着知识的生成.

由此可见，向量知识在不同模块中增加.知识内容从基本内容到规范定义,再从规范定义到知识推导,最后进行知识推广.不同模块中的教学内容是一个层层“螺旋式”生成的过程.

二、教学目标由低档到高级的“螺旋式”递增

有向线段的教学目标:学生简单了解用有向线段求最简单三角函数方程与简单三角不等式.目标简单低档.

平面向量的教学目标:学生在了解向量丰富的实际背景前提下,理解平面向量的概念及其运算法则;能用向量几何与代数语言和方法表述并解决数学和物理中的一些实际问题,发展运算能力和解决实际问题的能力.目标为理解加能用,属中级目标.

空间向量的教学目标:学生学会运用空间向量的方法处理立体几何中有关直线、平面位置关系的判断与求空间角与距离等度量的问题;体会向量方法在研究几何图形中的作用,培养和发展推理论证能力、逻辑思维能力、运用向量语言进行表达和交流的能力、空间想像能力和几何直观能力.目标为学会加体会,属综合高级目标.

空间向量的教学目标不仅是让学生在经历向量及其运算由平面向空间类比和推广,而且是学生在运用向量方法解决立体几何问题的过程中,感悟运算、推理在探索和发现中的作用,体会数学研究方法的模式化特点,感受理性思维的力量,提高数学素养.

以上介绍了向量在不同模块中的教学目标.教学从简单了解到能用,再到学会、体会.教学目标是一个层层“螺旋式”递增的过程.

黑龙江省冰雪旅游业发展过程中存在的一个突出问题就是：冰雪旅游文化和冰雪旅游资源的融合不够深入，没有形成相互依存，相互促进的良好发展态势。这就要求科学合进地规划：首先，对冰雪文化进行宣扬，通过冰雪节、冰雕节、冰雪摄影等艺术活动对冰雪文化进行宣扬，让广大群众增强对冰雪旅游文化的认同感；其次，结合黑龙江省的发展历史和地方特色，推出一整套统一和谐的文化体系，使得冰雪旅游发展过程中的文化融合具有良好的形态；最后，政府做好顶层设计，引导黑龙江省冰雪旅游文化和冰雪旅游产业发展的深度融合，形成以文化为依托，冰雪为表现的一种持续性特色冰雪产业。

三、教学要求由了解到应用的“螺旋式”提高

有向线段的教学要求:学生了解有向线段与其数量的概念,了解用有向线段几何表示正弦、余弦和正切.教学要求以了解为主.

平面向量的教学要求:了解向量的实际背景;理解平面向量的基本概念和几何表示;理解向量相等的含义.掌握向量加、减法和数乘运算,理解其几何意义;理解向量共线定理.了解向量的线性运算性质及其几何意义；了解平面向量的基本定理及其意义.掌握平面向量的正交分解及其坐标表示;会用坐标表示平面向量的加、减与数乘运算;理解用坐标表示的平面向量共线的条件(对线段定比分点坐标公式不作要求)；理解平面向量数量积的含义及其物理意义.掌握数量积的坐标表示,会进行平面向量数量积的运算;能利用数量积表示两个向量夹角的余弦,会用数量积判断两个非零向量是否垂直，了解向量是一种处理几何、物理等问题的工具.教学要求以理解、会用为主.

空间向量的教学要求:了解空间向量与平面向量的联系与区别;了解向量及其运算由平面向空间推广的过程.了解空间向量、共线向量、共面向量等概念;理解空间向量共线、共面的充要条件;了解空间向量的基本定理及其意义;掌握空间向量的正交分解及其坐标表示.掌握空间向量的线性运算及其性质;掌握空间向量的坐标运算.理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;掌握空间向量的数量积的坐标形式;能用向量的数量积判断向量的共线与垂直.理解直线的方向向量与平面的法向量的意义;会用待定系数法求平面的法向量.能用向量语言表述线线、线面、面面的垂直和平行关系.能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理);能用向量方法判断一些简单的空间线面的平行和垂直关系.能用向量方法解决线线、线面、面面的夹角的计算问题;体会向量方法在研究几何问题中的作用.教学要求以理解、掌握、能用为主.

以上介绍了向量在不同模块中的教学要求.从了解为主到理解、能用为主,再到理解、掌握、能用为主.教学要求是一个层层“螺旋式”提高的过程.

四、教学关注由表面到内涵的“螺旋式”拔节

有向线段的教学关注:从几何角度看有向线段是有方向,从代数角度看有向线段的数量可以取正数、负数和零.三角函数线就是用向量来表示角的正弦、余弦和正切值.关注的是向量的初步感知.

平面向量的教学关注:向量概念的教学应从物理背景和几何背景入手.物理背景是力、速度、加速度等概念；几何背景是有向线段.引导学生运用向量解决一些物理和几何问题.例如,利用向量计算力使物体沿某方向运动所做的功,利用向量解决平面内两条直线平行与垂直的位置关系等问题.相反，在中学阶段对于用向量解决较为复杂的平面几何问题要求很低.在向量的非正交分解、向量投影的概念只要求了解,无需展开,线段定比分点坐标公式及应用现行中学阶段不作要求.关注的是如何使向量符合从哪里来,再到哪里去的数学本质属性,是向量知识的内涵.

空间向量的教学关注:考虑到空间向量的线性运算及其性质、空间向量的数量积、空间向量的共线和垂直的充要条件等,与平面向量是基本一致的.因此,应引导学生类比猜想、自主探索,得出相应的性质和法则.

向量法解立体几何问题主要包括:证明一些定理(如空间位置关系的一些判定定理)和度量计算.教学时,应关注让学生体会向量的思想方法,不要过于追求解题技巧性.度量计算,只关注用向量法解决线线、线面、面面的夹角的计算,而不要过于强调解决有关距离的计算等问题.

引导学生学会运用类比、归纳等方法,经历向量及其运算由平面向空间推广的过程,体验数学在结构上的和谐性,弄清楚空间向量与平面向量的区别与联系.关注的是教学核心使学生学会学习.

以上介绍了向量在不同模块中的教学关注.从关注有向线段的向量的初步感知,到关注向量知识的内涵,再到关注学生的终身学习.教学关注在不同模块是一个层层“螺旋式”拔节提升的过程.

五、向量解法由简单到综合的“螺旋式”延展

向量既是高中数学知识体系中一部分,也是数学知识应用的数学思想方法之一.

向量法是从单纯的图形特征或代数特征求解延展到数形结合求解的主要数学方法.向量法含直接利用有向线段、向量基本知识求解的简单过程,也含有用向量的知识求解复杂问题的综合过程.它是既有平面中单纯的向量简单运算运用,也包含判断空间点、线、面的位置关系、求空间距离(点面、异面直线、线面和面面之间的距离)和空间角(异面直线、直线与平面和二面角等角)等综合应用.这些应用是含有由简单到综合的“螺旋式”延展过程.

再如，向量法推导两角差的余弦公式,体现了向量与三角相结合的综合应用过程.如图2,在直角坐标系xOy中,以x轴为始边分别作角α、β,终边分别与单位圆交于P1(cosα,sinα)、P2(cosβ,sinβ),则∠P1OP2=α-β.由于余弦函数是周期为2π的偶函数,所以,我们只需考虑0≤α-β<π的情况.

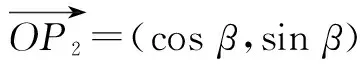
cos(α-β)=cosαcosβ+sinαsinβ,

这就是两角差的余弦公式.

如果说向量法推导两角差的余弦公式,是向量与三角两部分知识结合应用的过程,那么,用向量知识判断空间直线与直线、直线与平面、平面与平面的位置关系(平行、垂直),求空间角、距离等则是向量与几何结合的综合应用.这类例子很多，在此不再赘述.

(本文系江苏省教育科学“十二五”规划2015年度课题《高中数学概念研究性学习案例研究》)B-b/2015/02/203)成果)