巧用“分界点”解决一类含参讨论问题

◎朱 薇

(南海一中,广东 佛山 528000)

巧用“分界点”解决一类含参讨论问题

◎朱 薇

(南海一中,广东 佛山 528000)

对这类导函数涉及二次函数的分类讨论问题，首先要解决的任务是分类准确，有没有简便易操作的方法让学生轻松完成这个步骤？我们可以直接把以上三种情况“=0”时参数的值算出来就找到了参数的“分界点”.在已知条件下，用这些“分界点”去分参数，可以保证所分出来的类“不重不漏”.

分界点；函数；含参讨论

一、引出“分界点”的含义

例1 (2009年福建)点A为周长等于3的圆周上的一个定点，若在该圆周上随机取一点B，则劣弧的长度小于1的概率为________.

二、提出问题

例2 (2011年广东文)设a>0,讨论函数f(x)=lnx+a(1-a)x2-2(1-a)x的单调性.

【考点】利用导数研究函数的单调性.

解 定义域{x|x>0}.

设g(x)=2a(1-a)x2-2(1-a)x+1，x∈(0，+∞).

①若a=1，则g(x)=1>0,

∴在(0，+∞)上有f′(x)>0，即f(x)在(0，+∞)上是增函数.

②若a>1，则2a(1-a)<0，g(x)的图像开口向下，

此时Δ=[-2(1-a)]2-4×2a(1-a)×1=4(1-a)(1-3a)>0.

方程2a(1-a)x2-2(1-a)x+1=0有两个不等的实根,

③若00，g(x)的图像开口向上，

此时Δ=[-2(1-a)]2-4×2a(1-a)×1=4(1-a)(1-3a),

即f′(x)≥0，f(x)是增函数；

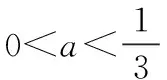
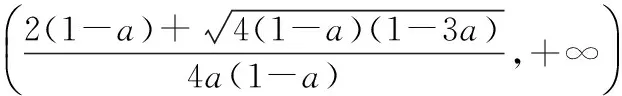
即f′(x)>0，f(x)是增函数；

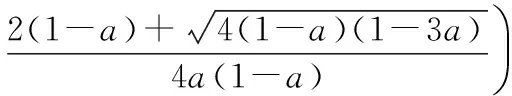
g(x)<0，即f′(x)<0，f(x)是减函数.

分析 这道题这里我们研究利用导数求单调区间的含参讨论问题，而这个导函数是灵活的二次函数.在这一题，不少高三同学是选择放弃或得分较低的，因为复习了一年，还是不能很好地处理，主要是突破不了对参数的分类.有些同学因为一直不是很会分，总是不敢下手，部分同学思路是有的，但因为这类题对思维的严谨性和完整性要求较高，所以有时考场一紧张，分类方面就多分或少分或分错而造成得分不高.

三、分析问题

思路突破：这道题在求好导函数和定义域后，其实本质就是解决导函数所对应的方程在定义域内根的分布问题.这时，我们需要画图，在确定图像时我们主要考虑三个问题：

1.二次项x2前面的系数是“>0”“=0”还是“<0”?(确定抛物线的开口方向)

2.判别式Δ是“>0”“=0”还是“<0”？(确定抛物线与x轴的交点情况)

3.定义域所在区间的端点函数值是“>0”“=0”还是“<0”？(确定抛物线与x轴的交点相对于定义域的分布，从而确定定义域内零点情况)

四、解决问题

事实上，我们可以直接把以上三种情况“=0”时参数的值算出来就找到了参数的“分界点”了.在已经条件下，用这些“分界点”去分参数，可以保证所分出来的类“不重不漏”.在正确的分类下，学生再往下处理，就会事半功倍.

题目 设a>0,讨论函数f(x)=lnx+a(1-a)x2-2(1-a)x的单调性.

解析 第一步：函数f(x)的定义域为(0，+∞)，

第二步：确定“分界点”.

(1)令二次项前面的系数2a(1-a)=0,解得：a=0或a=1.

(3)求出定义域(0,+∞)所在区间的端点函数值f′(0),若仍然含有参数a,继续令f′(0)=0，求出“分界点”.而此题f′(0)=1>0,说明此处没有“分界点”提供了.

五、总 结

本文主要希望通过比较直接的方法让大多数学生在含参分类讨论中学会使用“分界点”进行分类，做到不重不漏.其实，这种“分界点”的思想可以渗透到很多涉及不等关系的题目当中.要知道，解不等关系的基础是，先解等量关系，而我们同学最熟悉的莫过于“=”了.