有效建构意义 落实概念教学
赵玉飞

【关键词】概念教学 意义建构 有效性
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2015)10A-0114-01
在小學数学教学中,概念犹如知识网络中的纲,学生一旦掌握了概念,也就掌握了数学知识的基础部分。然而,在实际教学中,教师往往注重让学生认知和背诵概念,却忽视对概念意义的建构,导致知识之间缺乏联结,学生无法深刻理解概念的本质。如何有效落实概念教学,让学生深入学习并理解概念知识呢?笔者现根据自己的教学实践,谈三点看法。
一、引入具体素材,把握抽象本质
小学生的思维多停留在直观形象的层面上,在日常教学中,教师要引入具体的数学素材,帮助学生积累数学表象,通过丰富的数学表征的直观感知,让学生把握概念表征符号的抽象本质内涵,从而深刻理解数学概念。
例如,在教学苏教版三年级数学下册《平移和旋转》时,笔者根据学生的生活情境播放视频,画面上展现出各种游乐项目,有激流勇进、转盘、滑翔索道、弹射塔等,这些都是学生爱玩并且非常熟悉的游乐项目,笔者引导学生将这些运动项目分类。学生认为,可以将激流勇进、弹射塔、滑翔索道称作下滑类,将转盘和缆车分为旋转类。这时,笔者进一步引导学生思考:滑翔这类是什么移动?转盘这类又是什么移动?有什么区别?学生发现,这两类运动一类是位置的平移,另一类是物体的旋转。此时笔者让学生闭上眼睛,想象一下什么是平移,什么是旋转,而后让学生进行表演。有学生站起来向前走几步,认为这是平移;也有学生绕着一个点旋转,认为这是旋转。接下来,笔者让学生动手操作,进一步体验平移和旋转的本质区别。学生认为,平移是位置发生了改变,而旋转是围绕一个固定的点进行转动,但位置并没有发生变化。这样,学生不但积累了丰富的表象,对旋转和平移有了初步感知,而且能够把握表象的本质,找到平移和旋转的特征所在,为下一步学习“平移、旋转的运用”做好了铺垫。
二、巧用概念类比,突出概念重点
概念学习容易陷入一个误区,就是将概念背得滚瓜烂熟,但实际运用时往往又顾此失彼。为何会这样呢?主要是教师在教学中没有紧扣概念的重点,让学生对概念的特性有深刻体验。为此,教师要善于运用概念的类比,加深对概念的理解。
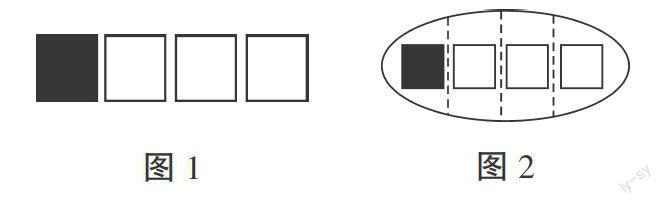
例如,在教学苏教版五年级数学下册《分数的意义》时,笔者设计了两个层次的教学进行概念类比:首先,让学生从一个物体的“1”扩展到一群物体的“1”。问:生活中有哪些物体的数量可以用“1”来表示?学生认为,一个班有38名学生,这个班就可以用“1”来表示……笔者追问:这个“1”代表什么?为什么?学生认为,一个物体或者一些物体可以被看做一个整体,这个整体通常就被叫做单位“1”。其次,让学生选择合适的单位“1”,完成从数1到单位“1”的实质性跨越。问:你能用图来表示吗?有学生将4个圆形看做一个整体,平均分为四等分,每一份就是;也有学生将8个苹果当做整体1,平均分成4份,每一份就是,就是2个苹果。此时笔者让学生思考:(如图1)把4个正方形平均分成4等分,其中的一份就是,你认为对吗?学生很快发现,这里的四等分并没有表示哪个是整体1。学生认为,只有将这四个等分的正方形圈起来才能表示是整体“1”(如图2).
通过这样的类比,学生深入理解了分数与单位“1”中包含的数量多少没有关系,只和它是否被平分为四等分,是否表示这样的“1”份有关。
三、有序整理回顾,培养概括能力
在小学数学概念教学中,教师要设计有效的教学活动,带领学生进行有序整理和回顾,培养学生的数学概括能力,发展数学思维。
例如,在教学苏教版五年级上册《小数的意义》时,笔者设计了这样的问题:
1分米=( )米=( )米 1分=( )元=( )元 1毫米=( )米=( )米
3分米=( )米=( )米 5分=( )元=( )元 8毫米=( )米=( )米
学生已经学过长度单位、人民币单位的换算,根据这种换算,学生认为,可以将1分米化为分数为,化为小数就是0.1米。此时笔者让学生思考:和0.1怎么表示长度?学生根据刻度画出线段图(如图3),从中可以看到,和0.1都表示1分米。
由此类推,笔者让学生展开探究:把1平分成10份,每份是( );把1平均分成100份,每份是( );把1平均分成1000份,每份是( ),学生根据图形,有序建构了小数计数单位所对应的小数数位,发展了学生的数学概念能力。
(责编 林 剑)

