关于等价边优美边裂图

温一慧

(苏州科技学院数理学院,江苏 苏州 215009)

0 引言

图的标号问题一直是图论中的热点问题,多年来引起了许多学者的兴趣和关注,新的问题也不断被提出,并取得了不少成果[1-14].注意到对于一般的图,其生成的边裂图有无穷多,由于没有有效方法,要判断这无穷多个边裂图的边优美性是困难的,尤其是非均匀边裂图.本文引进等价边优美边裂图的概念,阐述了等价边优美边裂图的存在性,并举例说明利用等价分类研究的方法,研究由某些图生成的无穷多边裂图的边优美性是可行的.

1 基本知识

定义1.1[1]设G=(V,E)是一个(p,q)简单图,双射h:E(G)→{1,2,3,…,q},h的诱导映射如果h+也是双射,则称G为边优美图.否则称为G非边优美图.

定义1.2[2]设G=(V,E)是一个(p,q)简单图,N是正整数集,映射f:E(G)→N,f(e)i=ki,ei∈E(G),ki∈N,定义G的边裂图SPE(G,f):令f(e)i=ki诱导的边集.

p(e)i={ei1,ei2,…,eikieij与ei的端点关联,j=1,2,…,ki},i=1,2,…,q,取,则称SPE(G,f)为G的边裂图.

若定义中映射f:E(G)→N,f(e)i=n0,n0>0是某个给定的整数,i=1,2,…,q,则称SPE(G,f)为G的均匀边裂图.否则称为非均匀边裂图.

设G=K1,3,映射f:E(K1,3)→N,f(e)i=ni,i=1,2,3,为了讨论的方面起见,也记为SPE(K1,3,f)为SPE(K1,3,f(n1,n2,n3)).

引理1.1[3]设G是一个(p,q)图,则G是边优美的必要条件是

q(q+1)≡ {0(mod p),P是奇数.p/2(mod p),P是偶数

2 主要结果

下面给出等价边优美边裂图的概念.并以非均匀边裂图SPE(K1,3,f)为例,说明等价边优美边裂图的存在性,利用等价分类方法讨论其无穷非均匀边裂图边优美性是可行的.

定义2.1 若边裂图G1与G2满足V(G1)=V(G2),E(G1)≤ E(G2),且G1与G2有相同的边优美性,则称G1与G2是等价边优美边裂图.

设{u0,u1,u2,u3}和{e1,e2,e3}={u0u1,u0u2,u0u3}分别是k1,3的顶点集和边集,其中u0是k1,3的中心.下面讨论中,设p=V(SPE(K1,3,f))=V(K1,3),q=E(SPE(K1,3,f)).

引理2.1 设n>1是任意整数,映射f:E(K1,3)→N,f(ei)=n,ei∈E(K1,3),i=1,2,3,则当且仅当n≡2(mod 4)或n≡3(mod 4),SPE(K1,3,f(n,n,n))是边优美的.

证明 1)若n≡2(mod 4),不妨设n=4k+2,k=0,1,2,…,此时p=4,q=3n=3(4k+2),对集合X={1,2,…,q},为了讨论方便,将其表成在模p意义下同余类[0],[1],[2],…,[p-1]的重集的形式:即

X={1,2,…,3(4k+2)}={(3k+2).[1],(3k+2).[2],(3k+1).[3],(3k+1).[0]}(mod4).分别构造f(ei)=n诱导的边集p(ei)的标号集Xi,i=1,2,3如下

X1={(2k+1).[1],(2k+1).[3]},则f+(u1)=0;

X2={(2k+1).[0],(2k+1).[2]},则f+(u2)=2;

X3=X(X1∪X2)={(k+1).[1],(k+1).[2],k.[3],k.[0]},

由于在(mod 4)意义下,(k+1).[1]+(k+1).[2]+k.[3]+k.[0]=[1]+(k+1).[2],因此,若k是奇数,有f+(u3)=1,f+(u0)=3;若k是偶数,有f+(u3)=3,f+(u0)=1.所以当n≡2(mod 4),SPE(K1,3,f(n,n,n))是边优美的.

2)若n≡3(mod 4),不妨设n=4k+3,k=0,1,2,…,此时q=3n=3(4k+3).当k=0,容易验证SPE(K1,3,f(3,3,3))是边优美的;若当k=1,2,…,令

Y={1,2,…,3(4k+3)}={(3k+3).[1],(3k+2).[2],(3k+2).[3],(3k+2).[0]}(mod4),构造边集p(ei)的标号集Yi,i=1,2,3如下

Y1={(2k+1).[1],(2k+1).[3],[0]},有f+(u1)=0;

Y2={2(k+1).[0],(2k+1).[2]},有f+(u2)=2;

Y3=Y(Y1∪Y2)={(k+2).[1],(k+1).[2],(k+1).[3],(k-1).[0]},

由于在(mod 4)意义下,(k+2).[1]+(k+1).[2]+(k+1).[3]+(k-1).[0]=[1]+(k+1).[2],因此当k是奇数时,有f+(u3)=1,f+(u0)=3;若k是偶数,有f+(u3)=3,f+(u0)=1.所以当n≡3(mod 4),SPE(K1,3,f(n,n,n))是边优美的.

3)若n≡0(mod 4)或n≡1(mod 4),由于此时q(q+1)≡0(mod 4),根据引理

1.1,SPE(K1,3,f(n,n,n))不是边优美的.

定理2.1 对任意整数n>1,SPE(K1,3,f(n,3n,3n)),SPE(K1,3,f(n,2n,4n))与SPE(K1,3,f(n,n,n))是等价边优美边裂图.

证明 先证明当且仅当n≡2(mod 4)或n≡3(mod 4),SPE(K1,3,f(n,3n,3n))是边优美的.

1)若n≡2(mod 4),设n=4k+2,k=0,1,2,…,q=7n=7(4k+2).令

A={1,2,…,7(4k+2)}={(7k+4).[1],(7k+4).[2],(7k+3).[3],(7k+3).[0]}(mod4),由引理2.1中X的定义,有AX={(4k+2).[1],(4k+2).[2],(4k+2).[3],(4k+2).[0]},将AX分成如下两个子集:A22={(4k+2).[1],(4k+2).[3]},A33={(4k+2).[0],(4k+2).[2]},注意到在(mod 4)意义下,(4k+2).[1]+(4k+2).[3]=[0],(4k+2).[0]+(4k+2).[2]=[0],因此构造SPE(K1,3,f(n,3n,3n))的标号集:A1=X1,A2=X2∪A22,A3=X3∪A33,其没有改变引理2.1中的f+(u1),f+(u2),f+(u3),f+(u0)的值,所以SPE(K1,3,f(n,3n,3n))是边优美的.

2)若n≡3(mod 4),设n=4k+3,k=0,1,2,…,有q=7n=7(4k+3).令

C={1,2,…,7(4k+3)}={(7k+6).[1],(7k+5).[2],(7k+5).[3],(7k+5).[0]}(mod4),由引理2.1中Y的定义,有CY={(4k+3).[1],(4k+3).[2],(4k+3).[3],(4k+3).[0]},将CY分成如下两个子集:C22={(4k+3).[1],(4k+3).[3]},C33={(4k+3).[0],(4k+3).[2]},由于在(mod 4)意义下,(4k+3).[1]+(4k+3).[3]=[0],(4k+3).[0]+(4k+3).[2]=[2],因此构造SPE(K1,3,f(n,3n,3n))的标号集:C1=Y1,C2=Y2∪C22,C3=Y3∪C33,与引理2.1证明过程比较:f+(u3)与f+(u0)的值互换,f+(u1)和f+(u2)的值不变,所以SPE(K1,3,f(n,3n,3n))仍是边优美的.

对于SPE(K1,3,f(n,2n,4n)),只需将上面证明中的A33的子集{(4k+2).[0]}与C33的子集 {(4k+3).[0]},分别并入A22和C22,运用同样方法,可得SPE(K1,3,f(n,2n,4n))是边优美的.

若n≡0(mod 4),或n≡1(mod 4),SPE(K1,3,f(n,3n,3n))和SPE(K1,3,f(n,2n,4n))不满足边优美的必要条件.

据定义2.1和引理2.1,对任意整数n>1,SPE(K1,3,f(n,3n,3n)),SPE(K1,3,f(n,2n,4n))与SPE(K1,3,f(n,n,n))是等价边优美边裂图.

定理2.2 对任意整数n>1,SPE(K1,3,f(n,n,5n))与SPE(K1,3,f(n,n,n))是等价边优美边裂图.

证明 事实上,若n≡2(mod 4),设n=4k+2,k=0,1,2,…,将SPE(K1,3,f(n,n,5n))与SPE(K1,3,f(n,n,n))比较,前者比后者的一条悬边增加了4n条裂边,增加的4n条裂边的标号和是[0](在(mod 4)意义下),说明增加的4n条裂边的标号不改变f+(u1)的值,i=0,1,2,3.

若n≡3(mod 4),设n=4k+3,k=0,1,2,…,不失一般性,设f(e3)=5n,由于SPE(K1,3,f(n,n,5n))比SPE(K1,3,f(n,n,n))增加了4n条裂边,裂边的标号和是(4k+3).[2](在(mod4)意义下),注意到4k+3是奇数,与引理2.1证明比较:f+(u3)与f+(u0)的值互换,f+(u1)和f+(u2)的值不变,所以SPE(K1,3,f(n,n,5n))仍是边优美的.

引理2.2 对任意整数n≥1,SPE(K1,3,f(n,n,2n))不是边优美的.

证明 由于q(q+1)≡0(mod 4),据引理1.1,SPE(K1,3,f(n,n,2n))不是边优美的.

引理2.3 对任意整数n≥1,当且仅当n≡1(mod 4)或n≡2(mod 4),SPE(K1,3,f(n,n,3n))是边优美的.

证明 若n≡1(mod 4),设n=4k+1,k=0,1,2,….q=5n=5(4k+1).令Z={1,2,…,5(4k+1)}={(5k+2).[1],(5k+1).[2],(5k+1).[3],(5k+1).[0]}(mod4),构造边集p(ei)的标号集Zi,i=1,2,3如下

Z1={(4k+1).[0]},有f+(u1)=0;Z2={(4k+1).[2]},有f+(u2)=2;

Z3=Z(Z1∪Z2)={(5k+2).[1],k.[2],(5k+1).[3],k.[0]},

由于在(mod 4)意义下,(5k+2).[1]+k.[2]+(5k+1).[3]+k.[0]=[1]+k.[2],因此,当k是奇数,有f+(u3)=3,f+(u0)=1;当k是偶数,有f+(u3)=1,f+(u0)=3.

若n≡2(mod 4),设n=4k+2,k=0,1,2,….q=5n=5(4k+2).令

在课堂中引入英美文学的鉴赏，可以极大地提高学生的综合素质与素养，通过老师的进一步讲解，学生能够更深入地了解英美文化中的丰富寓意。当代社会风气普遍浮躁，学生也不例外。学生对人生、世界的看法往往不成熟，所以更需要从文学名著中汲取养分，致力于完善自身的素质。

D={1,2,…,5(4k+2)}={(5k+3).[1],(5k+3).[2],(5k+2).[3],(5k+2).[0]}(mod4),构造边集p(ei)的标号集Di,i=1,2,3,如下

D1={(4k+2).[0]},有f+(u1)=0;D2={(4k+2).[3]},有f+(u2)=2;D3=D(D1∪D2)={(5k+3).[1],(5k+3).[2],k.[3],k.[0]},

由于在(mod 4)意义下,(5k+3).[1]+(5k+3).[2]+k.[3]+k.[0]=3.[1]+(5k+3).[2],故当k是奇数,5k+3是偶数,有f+(u3)=3,f+(u0)=1;当k是偶数,5k+3是奇数,有f+(u3)=1,f+(u0)=3.

若n≡0(mod 4)或n≡3(mod 4),均有q(q+1)≡0(mod 4),据引理1.1,SPE(K1,3,f(n,n,3n))不是边优美的.故当且仅当n≡1(mod 4)或n≡2(mod 4),SPE(K1,3,f(n,n,3n))是边优美的.

定理2.3 对任意整数n≥1,SPE(K1,3,f(n,2n,2n))与SPE(K1,3,f(n,n,3n))是等价边优美边裂图.

证明 由引理2.3的证明,若n≡1(mod 4),构造边集p(ei)的标号集Ti,i=1,2,3如下,取

T1=Z1={4k+1).[0]},有f+(u1)=0;T2={4k+2).[1],4k.[2]},有f+(u2)=2;T3=Z(T1∪T2)={k.[1],(k+1).[2],(5k+1).[3],k.[0]},

由于在(mod 4)意义下,k.[1]+(k+1).[2]+(5k+1).[3]+k.[0]=[3]+(k+1).[2],因此,当k是奇数,有f+(u3)=3,f+(u0)=1;当k是偶数,有f+(u3)=1,f+(u0)=3.

若n≡2(mod 4),构造边集p(ei)的标号集Si,i=1,2,3,如下,由引理2.3的证明,取

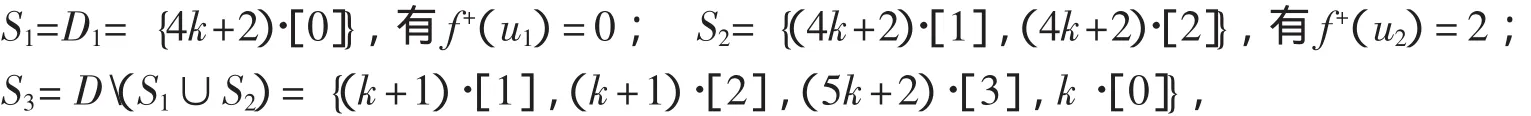
由于在(mod 4)意义下,(k+1).[1]+(k+1).[2]+(5k+2).[3]+k.[0]=[3]+(k+1).[2],因此当k是奇数,有f+(u3)=3,f+(u0)=1;当k是偶数,有f+(u3)=1,f+(u0)=3.

若n≡0(mod 4)或n≡3(mod 4),均有q(q+1)≡0(mod 4),SPE(K1,3,f(n,2n,2n))不是边优美的.据定义2.1和引理2.3,对于n≥1,SPE(K1,3,f(n,2n,2n))与SPE(K1,3,f(n,n,3n))是等价边优美边裂图.

引理2.4 设任意整数n≥1,则当且仅当n≡1(mod 4)或n≡3(mod 4),SPE(K1,3,f(n,n,4n))是边优美的.

证明 若n≡1(mod 4),设n=4k+1,k=0,1,2,….q=6n=6(4k+1).令H={1,2,…,6(4k+1)}={(6k+2).[1],(6k+2).[2],(6k+1).[3],(6k+1).[0]}(mod4),构造边集p(ei)的标号集Hi,i=1,2,3如下

H1={(4k+1).[0]},有f+(u1)=0;H2={(4k+1).[2]},有f+(u2)=2;H3=H(H1∪H2)={(6k+2).[1],(2k+1).[2],(6k+1).[3],2k.[0]},

由于在(mod 4)意义下,(6k+2).[1]+(2k+1).[2]+(6k+1).[3]+2k.[0]=[1]+(2k+1).[2],因此,有f+(u3)=3,f+(u0)=1.

若n≡3(mod 4),设n=4k+3,k=0,1,2,….q=6n=6(4k+3).令

R={1,2,…,6(4k+3)}={(6k+5).[1],(6k+5).[2],(6k+4).[3],(6k+4).[0]}(mod4),构造边集p(ei)的标号集Ri,i=1,2,3如下,

R1={(4k+3).[0]},有f+(u1)=0;R2={(4k+3).[2]},有f+(u2)=2;R3=R(R1∪R2)={(6k+5).[1],2(k+1).[2],(6k+4).[3],(2k+1).[0]},

由于在(mod4)意义下,(6k+5).[1]+2(k+1).[2]+(6k+4).[3]+(2k+1).[0]=[1]+2(k+1).[2],因此,有f+(u3)=1,f+(u0)=3.

若n≡0(mod 4)或n≡2(mod 4),均有q(q+1)≡0(mod 4),SPE(K1,3,f(n,n,4n))不是边优美的.故当且仅当n≡1(mod 4)或n≡3(mod 4),SPE(K1,3,f(n,n,4n))是边优美的.

定理2.4 对任意整数n≥1,SPE(K1,3,f(n,2n,3n))与SPE(K1,3,f(n,n,4n))是等价边优美边裂图.

证明 由引理2.4的证明,若n≡1(mod4),构造边集p(ei)的标号集Fi,i=1,2,3如下

F1={(4k+1).[2]},有f+(u1)=2;F2={(4k+1).[1],(4k+1).[3]},有f+(u2)=0;F3=H(F1∪F2)={(2k+1).[1],(2k+1).[2],2k.[3],(6k+1).[0]},

由于在(mod 4)意义下,(2k+1).[1]+(2k+1).[2]+2k.[3]+(6k+1).[0]=[1]+(2k+1).[2],因此有f+(u3)=3,f+(u0)=1.

若n≡3(mod 4),构造边集p(ei)的标号集Bi,i=1,2,3,如下,由引理2.4的证明,取

B1={(4k+3).[2]},有f+(u1)=2;B2={(4k+3).[1],(4k+3).[3]},有f+(u2)=0;B3=R(B1∪B2)={2(k+1).[1],2(k+1).[2],(2k+1).[3],(6k+4).[0]},

由于在(mod4)意义下,2(k+1).[1]+2(k+1).[2]+(2k+1).[3]+(6k+4).[0]=[1]+2(k+1).[2],因此有f+(u3)=1,f+(u0)=3.

若n≡0(mod4)或n≡2(mod4),均有q(q+1)≡0(mod4),SPE(K1,3,f(n,2n,3n)),不是边优美的,故由定义2.1和引理2.4,SPE(K1,3,f(n,2n,3n))与SPE(K1,3,f(n,n,4n))是等价边优美边裂图.

根据引理2.1~2.4及定理2.2,采用上面同样的方法,可得

推论2.5 对任意整数n>1,t≥1,

1)若t≡1(mod4),则当且仅当n≡2(mod4)或n≡3(mod4),SPE(K1,3,f(n,n,tn))是边优美的.

2)若t≡2(mod4),则SPE(K1,3,f(n,n,tn))不是边优美的.

3)若t≡3(mod4),则当且仅当n≡1(mod4)或n≡2(mod4),SPE(K1,3,f(n,n,tn))是边优美的.

4)若t≡0(mod4),则当且仅当n≡1(mod4)或n≡3(mod4),SPE(K1,3,f(n,n,tn))是边优美的.

根据定理2.1和定理2.3,可得

推论2.6 对任意整数n>1,s≥1,

1)若s≡0(mod2),当且仅当n≡1(mod4)或n≡2(mod4),SPE(K1,3,f(n,sn,sn))是边优美的.

2)若s≡1(mod2),当且仅当n≡2(mod4)或n≡3(mod4),SPE(K1,3,f(n,sn,sn))是边优美的.

根据引理2.2和定理2.4,可得

推论2.7 设任意整数n≥1,r≥2,则

1)若r≡0(mod2),SPE(K1,3,f(n,(r-1)n,rn))不是边优美的.

2)若r≡1(mod2),当且仅当n≡1(mod4)或n≡3(mod4),SPE(K1,3,f(n,(r-1)n,rn))是边优美的.

根据引理2.1~2.4,定理2.1~2.4与推论2.5~2.7,可得

推论2.8 对任意整数n、s、t>1,SPE(K1,3,f(n,sn,tn))与SPE(K1,3,f(n,n,(s+t-1)n))是等价边优美边裂图.

限于篇幅,讨论从略.感兴趣的读者还可以继续验证下面的结果

定理2.9 设任意整数n>1,r≥1,则

1)若r≡0(mod4),则当且仅当n≡2(mod4)或n≡3(mod4),SPE(K1,3,f(n,n,n+r))是边优美的.

2)若r≡1(mod4),则当且仅当n≡0(mod4)或n≡3(mod4),SPE(K1,3,f(n,n,n+r))是边优美的.

3)若r≡2(mod4),则当且仅当n≡0(mod4)或n≡1(mod4),SPE(K1,3,f(n,n,n+r))是边优美的.

4)若r≡3(mod4),则当且仅当n≡1(mod4)或n≡2(mod4),SPE(K1,3,f(n,n,n+r))是边优美的.

定理2.10 若(s+t)≡r(mod 4),则SPE(K1,3,f(n,n+s,n+t))与SPE(K1,3,f(n,n,n+r))是等价边优美边裂图,其中n>1,s≥1,t≥1是任意整数.

[1]Lo S P.On edge-graceful labelings of graphs[J].Congressus Numerantium,1985,50:231-241.

[2]Wen Y H,Lee S M,Sun H.On the supermagic edge-splitting extension of graphs[J].Ars Combinatoria,2006,79:115-128.

[3]Lee L M,Lee S M,Murty G.On edge-graceful labelings of complete graphs-solutions of Lo's conjecture[J].Congressum Numerantum,1988,62:225-233.

[4]严谦泰.积图PnXPm的奇优美性和奇强协调性[J].系统科学与数学,2010,30(3):341-348.

[5]魏丽侠,张昆龙.几类并图的优美标号[J].中山大学学报:自然科学版,2008,47(3):10-13.

[6]程辉,姚兵,张忠辅.核图与L(2,1)标号[J].兰州大学学报:自然科学版,2008,44(2):94-97.

[7]温一慧,康庆德.关于广义蝶图的平衡指标集[J].数学研究与评论,2009,29(2):202-212.

[8]Wen Y H,Lee S M,Su H H.On Z2⊕ Z2–magic Graphs[J].Congressus Numerantium,2009,199:13-31.

[9]Lee S M,Hokuen N,Wen Y H.On the edge-magic indices of(v,v+1)-graphs[J].Utilitas Mathematica,2007,72:97-110.

[10]刘家保,王林.一类图的边幻和标号及其算法[J].汕头大学学报:自然科学版,2011,26(3):29-34.

[11]温一慧.关于广义轮图的友好性[J].兰州大学学报:自然科学版,2008,44(3):103-108.

[12]温一慧.一类边裂图边优美性的充要条件[J].数学的实践与认识,2009,39(19):197-202.

[13]温一慧.关于图的一致平衡性[J].数学季刊,2010,25(4):565-571.

[14]温一慧.组合.算法.理论与应用[M].兰州:兰州大学出版社,2006:359-378.