任意阶自催化反应扩散系统的正平衡态
鲁元海
(中山市东区中学,广东 中山 528403)
0 引言
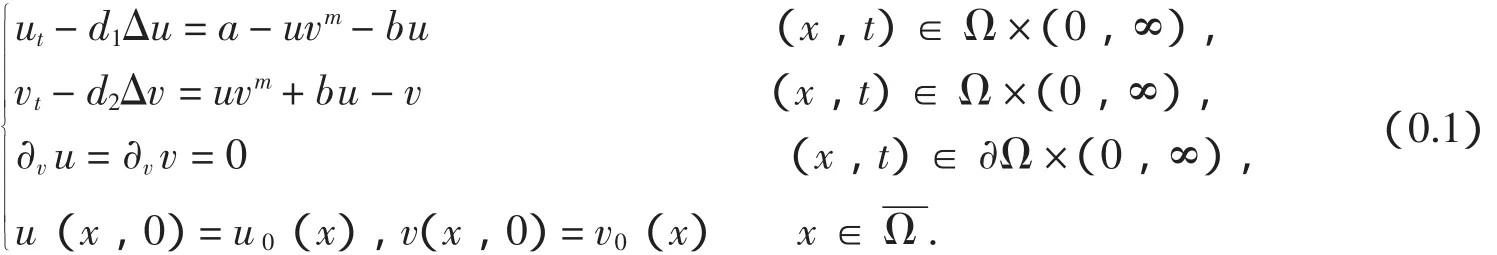
本文考虑如下化学系统其中Ω⊂RN(N≥1)是一个具有光滑边界∂Ω的有界区域.u和v分别表示反应物和催化剂的浓度.v为Ω的单位外法向量,Δ为Laplace算子.齐次Neumann边界条件表示这个系统是封闭的.d1,d2是扩散系数.m为催化剂的阶数.a,b,m,d1,d2均为正常数.初值u0(x),v0(x)是不恒为零且在上光滑的函数.
若m取正整数,当m>1时模型(0.1)为高次自催化反应模型[1].特别地,当m=2时,模型(0.1)成为低浓度三分子模型[2-3].但在实际化学反应模型中m的阶数是由实验确定的,因此m不一定是正整数[4].这里考虑一般情形即m>0为任意正数.
系统(0.1)对应的平衡态系统为

1 稳定性分析
设0=μ0<μ1<μ2<…为算子-Δ在Ω上带有齐次Neumann边界条件的特征值,其中Δ为拉普拉斯算子.令Xj是对应于μj的特征空间
v=0在∂Ω上},{φjll=1,…,m(μj)}是Xj的一个正交基底,其中m(μj)表示特征值μj的重数,且
由抛物型方程标准理论可知(0.1)存在唯一非负全局解(u,v).本节研究系统(0.1)的常数正解(u*,v*)的稳定性.
定理1.1 若条件mam<(am+b)(am+b+1)和
成立,则系统(0.1)的常数正解(u*,v*)是一致渐近稳定的.
证明 将(0.1)在(u*,v*)处线性化为
这里gi(y1,y2)=O(y12+y22),i=1,2.对每个j(j=0,1,2,…),Xj是算子L的不变子空间.ξj是L在Xj上的一个特征值当且仅当ξj是矩阵Aj的一个特征值,其中
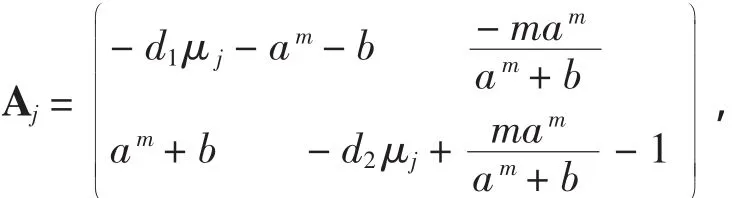
也就是,ξj满足如下方程
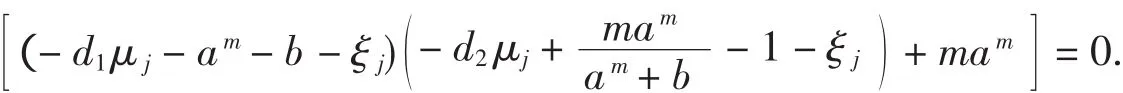
简单的计算可得
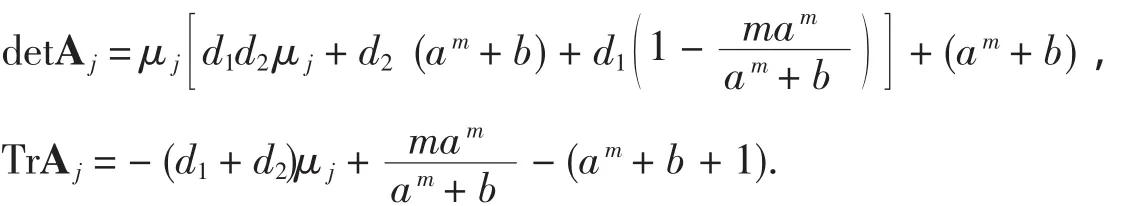
这里detAj和TrAj分别是Aj的行列式和迹.注意到μ0=0,容易得到在定理条件下detAj>0和TrAj<0成立.类似于文献[5]的分析,存在一个不依赖于j的正数σ使得算子L的特征值分布于{Reξ<-σ}.所以(u*,v*)是一致渐近稳定的,定理得证.
当0 推论1.1 若0 注 由推论1.1,当0 本节主要研究系统(0.2)的任一正解的上下界.先给出如下引理.引理2.1(最大值原理[6)]设g∈C(XR). (i)假定w∈C(2Ω)∩C(1)满足 Δw(x)+g(x,w(x))≥0,x∈Ω;∂vw≤0,x∈∂Ω.若w(x0)=maxΩw,则g(x0,w(x0))≥0.(ii)假定w∈C(2Ω)∩C(1)满足 Δw(x)+g(x,w(x))≤0,x∈Ω;∂vw≥0,x∈∂Ω.若w(x0)=minΩw,则g(x0,w(x0))≤0.定理2.1 系统(0.2)的任意正解(u,v)满足 证明 假定(u,v)是(0.2)的一个正解.令u(x1)=ma xu,v(x)2=ma xv,u(y)1=mi nu, Ω Ω Ω v(y2)=mi nv.将引理2.1应用到(0.2)的第一个方程,得a-u(x)1v(mx)1-bu(x)1≥0,即 Ω 令φ=d1u+d2v.将(0.2)的两个方程相加,得 设x3∈是φ的最大值点.由引理2.1,有a-v(x3)≥0,即v(x3)≤a.又由(2.1),可得 因此 另一方面,由(0.2)的第一个方程和引理2.1,有a-u(y1)vm(y1)-bu(y1)≤0,也就是a≤u(y1)(b+vm(y1)),与式(2.2)联立得 下面再由(0.2)的第二个方程和引理2.1,得u(y2)vm(y2)+bu(y2)-v(y2)≤0.由式(2.3)有 由式(2.1)-(2.4),可知定理结论成立. 由定理2.1容易得到如下推论. 推论2.1 固定a,b,m,D1,D2>0,则存在依赖于a,b,m,D1,D2的两个正常数C1,C2,使得当0 本节利用隐函数定理证明当d2很大时系统(0.2)不存在非常数正解(参看文献[7]).首先证明如下结论. 引理3.1 固定a,b,m和d1.设(ui,v)i是系统(0.2)对应于d2=d2,i的正解,其中当i→∞时,d2,i→∞. 则当i→∞时,(ui,v)i→ (u*,v*)于[C(2)]2中. 证明 由定理2.1、标准的椭圆型方程正则性理论及嵌入定理,存在(ui,v)i的一个子列,仍记为它本身,使得当i→∞时,(ui,v)i→(u,v)于[C2()]2中.因d2,i→∞,故有v≡δ,这里δ是正常数.(u,δ)满足 定理3.1 固定a,b,m,d1>0,存在依赖于a,b,m,d1和Ω的D>0,当d2>D时系统(0.2)不存在非常数正解. 设Φ是F在(0,u*,0,v*)处关于(u,v~,ξ)的Frechet导数.容易得到 为了能利用隐函数定理,须验证Φ既是单射又是满射.事实上,假定下面将证明,u∧=ξ∧=0,便可知Φ可逆.因为v∧≡0,所以Φ变为 v*)是方程在[0,ρ0]XBr0(u*,0,v*)中的唯一解.这里Br0(u*,0,v*)表示在W2v,(2Ω)XW2v,,2(0Ω)XR+中以(u*,0,v*)为中心,以r0为半径的开球.若有必要可取更小的ρ0,r0,由引理3.1便可得定理3.1的结论. 本节研究(0.2)非常数正解的存在性.为此,首先给出如下预备知识.记 及 则有DuG(u*)=A,且(0.2)可写为 u是(4.1)的一个正解当且仅当F(u):=u-(I-Δ)-1(G(u)+u)=0,这里(I-Δ)-1是I-Δ具其次Neumann边界条件的逆.直接的计算表明 为了利用度理论得到非常数正解的存在性,我们首先计算F(u)在u*处的指数.由Leray-Schauder定理[8],可知若0不是(4.2)的特征值,则index(F,u*)=(-1)r,这里r是(4.2)的负特征值的个数. 直接的计算表明,对每个整数j≥0,Xj在DuF(u*)的作用下是不变空间,ξj是DuF(u*)在Xj上的一个特征值当且仅当它是矩阵(1+μj)-1(μjI-A)的一个特征值.因此DuF(u*)是可逆的当且仅当对任意j≥0,矩阵(1+μj)-1(μjI-A)是非奇异的.记 并且若H(a,b,m,d1,d2,μj)≠0,DuF(u*)在Xj上的负特征值的个数是奇数当且仅当H(a,b,m,d1,d2,μj)<0.采用类似于文献[9]的论述,可证明下面性质成立. 命题4.1 假设对所有整数j≥0矩阵MjI-A非奇异.m(μj)是特征值μj的代数重数.则 为了计算index(F(.),u*),应考虑H(a,b,m,d1,d2,μ)的符号.显然有 若 及 成立,则H(a,b,m,d1,d2,μ)=0恰有两个正解μ1*<μ2*,其中μ1*,μ2*表示如下: 且H(a,b,m,d1,d2,μ)<0当且仅当μ∈(μ1*,μ2*),由式(4.4)及(4.5)可得 即 注 若m>1及(1-m)am+b<0成立.则当d2很小或者d1很大时(4.6)成立.利用文献[5]中的方法,可得本节的主要结论如下: 定理4.1 设m>1,式(4.6)成立,且存在0≤i 证明 由定理3.1及(4.3),固定充分大的D,使得系统(0.2)当d2=D时没有非常数正解且对任意μ≥0都有H(a,b,m,d1,D,μ)>0成立.由推论2.1知,存在依赖于 ∧∧a,b,m,d1,d2的M>0,使得对任意d>d2,系统(0.2)具有扩散系数d1及d时,其任意正解(u,v)在上满足M-1 求解系统(0.2)等价于寻找Φ(1,.)在Θ上的一个不动点.而且从Θ的定义以及推论2.1可知对所有0≤t≤1,Φ(1,.)的在∂Θ上没有不动点.因Φ(t,.):[0,1]X Θ→[C(1)]2是紧的,度deg(I-Φ(t,.),Θ,0)有定义.所以由拓扑度的同伦不变性可得 由D的选择可知,H(a,b,m,d1,D,μ)>0,且u*是Φ(0,.)的唯一不动点.由命题4.1得 相反地,假设(0.2)没有非常数正解,再由命题4.1可知 由(4.8)-(4.10)得出矛盾.因此(0.2)至少存在一个非常数正解,定理得证. 文章研究了一个自催化化学反应扩散系统的平衡态问题,其中催化剂的阶数是任意正实数.下面总结出扩散系数及催化剂阶数对模式生成的影响,并希望能展示出化学系统中模式生成的一些有趣现象.首先,由推论1.1,催化剂阶数在模式生成中起着重要的作用.确切地讲,当0 [1]张丽,刘三阳.一类高次自催化耦合反应扩散系统的分歧和斑图[J].应用数学和力学,2007,28(9):1102-1113. [2]张棣,陈洽融.低浓度三分子反应模型[J].科学通报,1982(21):1281-1284. [3]陈兰荪,王东达.一个生物化学反应的振动现象[J].数学物理学报,1985,5(3):261-266. [4]Kay A L,Needham D J,Leach J A.Travelling waves for a coupled,singular reaction-diffusion system arising from amodeloffractionalorderautocatalysiswith decay:I. Permanentform travelling waves[J].Nonlinearity,2003,16(2):735-770. [5]Wang M X.Non-constant positive steady-states of the Sel'kov model[J].Journal of Differential Equations,2003,190(2):600-620. [6]Lou Y,Ni W M.Diffusion vs.cross-diffusion:an elliptic approach[J].Journal of Differential Equations,1999,154:157-190. [7]Peng R,Wang M X.Positive steady-state solutions of the Noyes-Field model for Belousov-Zhabotinskii reaction[J].Nonlinear Analysis,2004,56(3):451-464. [8]Nirenberg L.Topics in Nonlinear Functional Analysis[M].American Mathematical Society,Providence,RI:2001. [9]Pang P Y H,Wang M X.Qualitative analysis of a ratio-dependent predator-prey system with diffusion[J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics.2003,133(4):919-942.2 先验估计
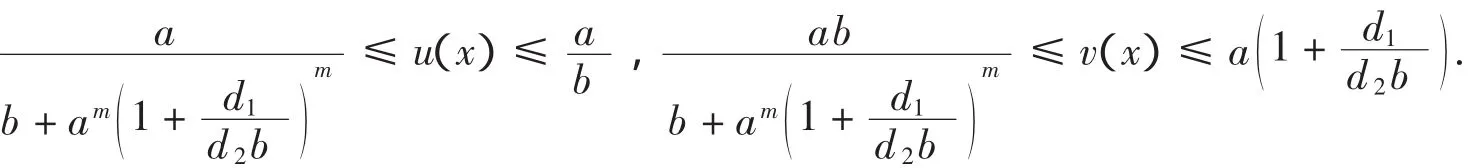

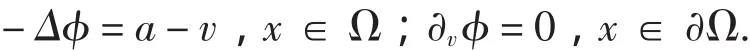
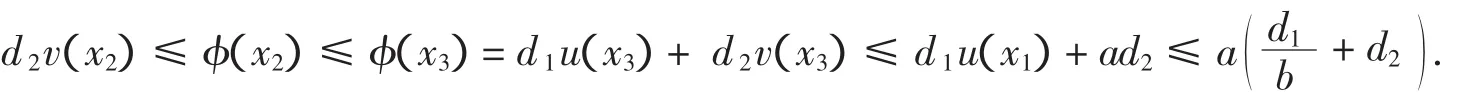



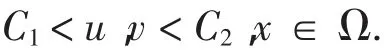
3 非常数正解的不存在性
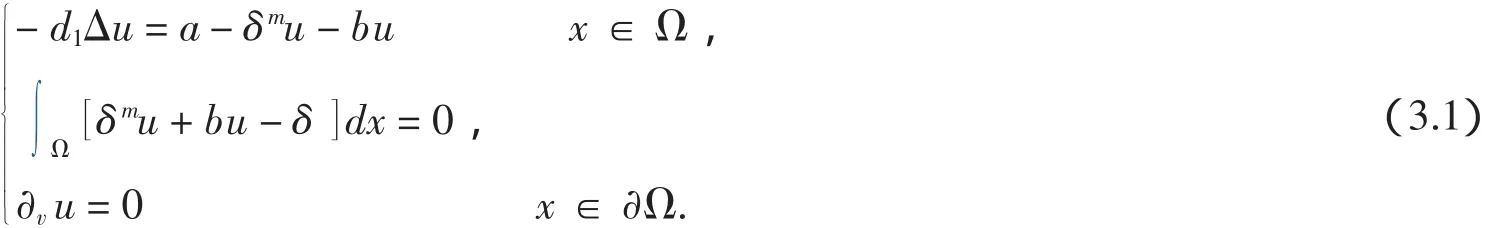
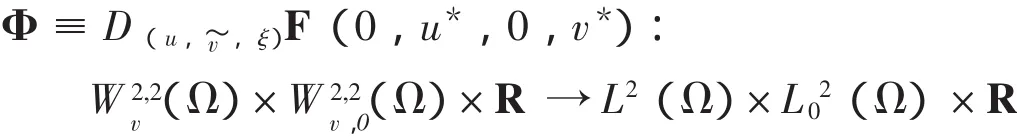
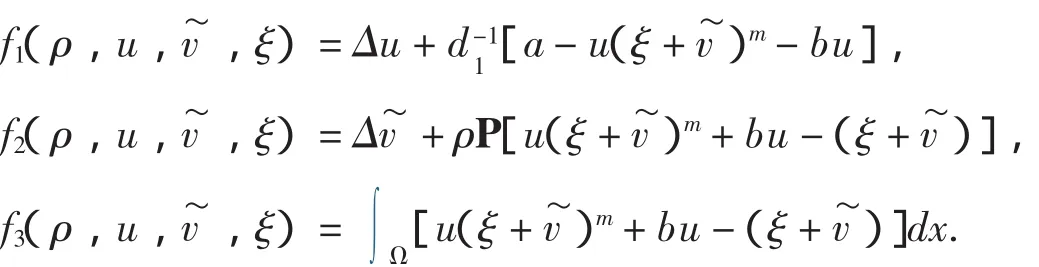
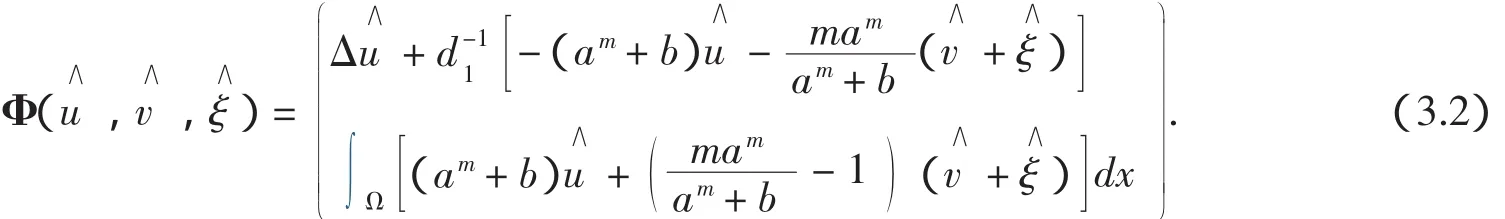
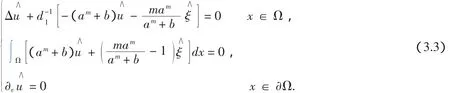
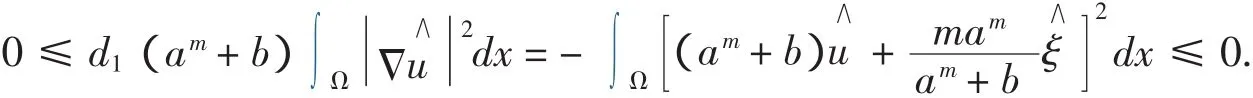
4 非常数正解的存在性
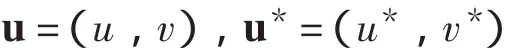
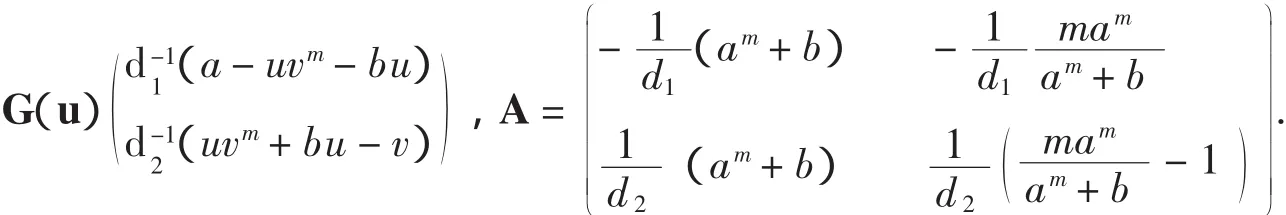


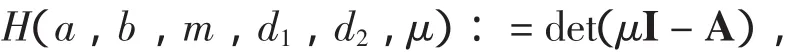
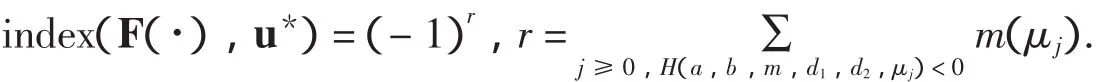
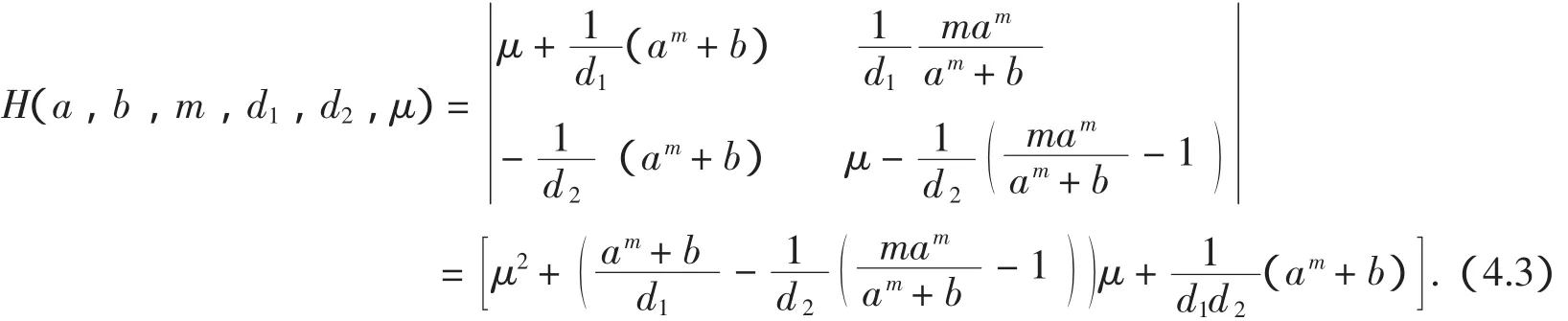


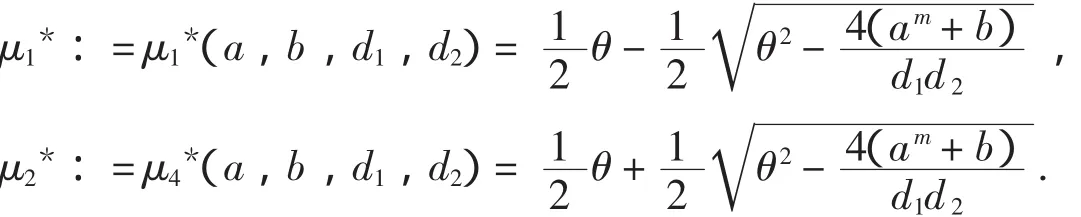
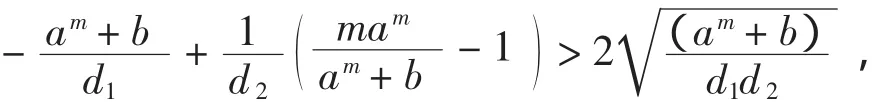

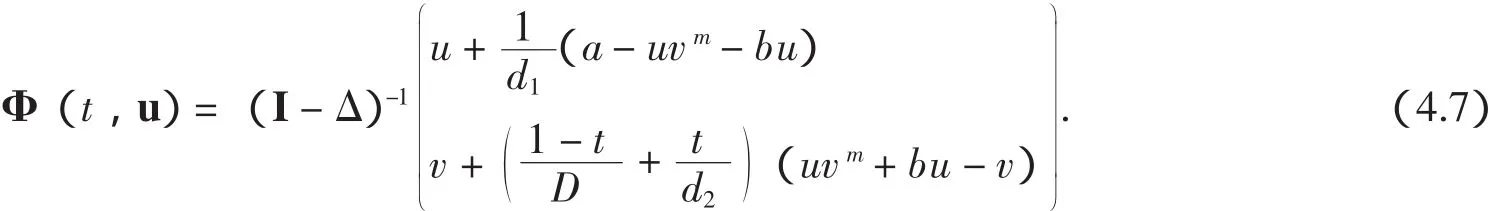
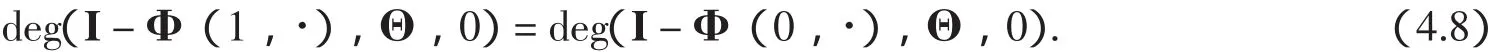

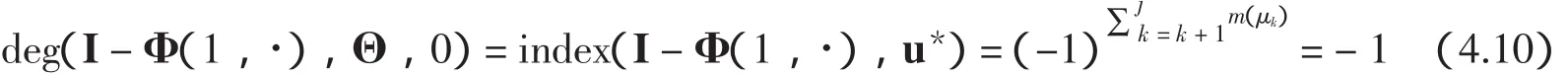
5 结论

