关于动态电路阶数的讨论
田社平,孙 盾,张 峰
(1.上海交通大学电子信息与电气工程学院,上海 200240;2浙江大学电气工程学院,浙江杭州 310027)
动态电路可以用微分方程加以描述。根据描述电路的微分方程的阶数,可以将电路分为一阶电路、二阶电路等。现行电路教材几乎均以此来定义动态电路的阶数,如“用一阶常微分方程描述的电路称为一阶电路”(文献[1-3])或“如果电路的输入—输出方程是一阶微分方程,则称该电路为一阶电路。如果电路的输入—输出方程是n阶微分方程,则称该电路为n阶电路”(文献[4])。
笔者在教学中发现,一个动态电路往往存在多个电压变量和电流变量,当描述所有这些电压变量和电流变量的微分方程的阶数都相同时,上述定义是准确的,但是也有一些特别的电路,其电路变量的微分方程的阶数并不相同,这样上述定义则无法准确地描述动态电路的阶数。
不失一般性,本文仅以线性非时变动态电路为例加以讨论。
1 实例分析
考虑如图1所示的电路,假设R1=R2=1Ω,R3=4Ω,C1=C2=1F,L=1H。下面分析描述电路变量i,uC1和uC2的微分方程表达式。

图1 动态电路之一
列写电路的KCL方程:

列写KVL方程:
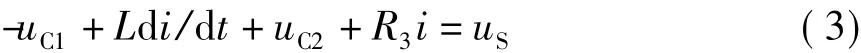
将元件参数值代入式(1)~式(3)并整理得

对式(6)两边微分,并将式(4)和式(5)代入,整理后可得
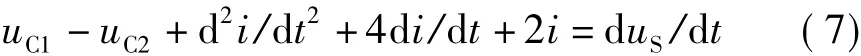
将式(6)和式(7)相加,得到描述电流变量i的微分方程为

将式(4)中的电流i代入式(8),得到描述电压变量uC1的微分方程为

类似可得到描述电压变量uC2的微分方程为

由式(8)~式(10)可以看出,描述电流变量i的微分方程的阶数为2,而描述电压变量uC1和uC2的微分方程的阶数为3,两者并不相等。而观察图1所示电路,可知该电路包含三个独立的动态元件,说明该电路是一个三阶电路。
2 动态电路阶数的确定
由上面讨论可知,电路变量的阶数和电路的阶数并不完全相同。对动态电路的阶数的判定,一般可采用如下四种方法。
(1)通过观察电路,确定电路中独立动态元件的个数,它也是电路的阶数。这是一种常用的方法,适用于大多数电路。
(2)以电路变量的阶数的最大值作为电路的阶数。本文上一节的分析就采用了这种方法。
(3)用零输入电路确定电路的阶数[5]。电路的阶数与电路的激励大小无关,因此可以将电路的激励置零,然后再确定电路的阶数。
(4)电路的阶数等于电路的非零固有频率数。因此,求出电路的非零固有频率数,也就得到了电路的阶数。
下面就后面两种方法进行讨论。
图2所示为包含两个电容的电路,其中图2(a)电路的激励为电压源,初看此电路,似乎两个电容独立,但将电压源置零后发现,两个电阻、两个电容为并联关系,因此该电路为一阶电路。图2(b)电路的激励为电流源,如果将电流源置零,则R1、C1和R2、C2构成两个独立的回路,该电路是二阶电路。如果两个回路的时间常数相等,即R1C1=R2C2时,该电路退化为一阶电路。
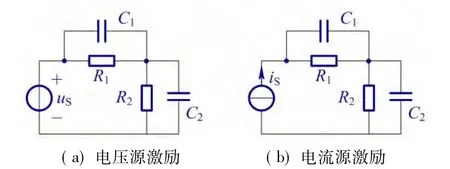
图2 动态电路之二
图3所示为一含受控源的电路,该电路中没有画出激励[4]。
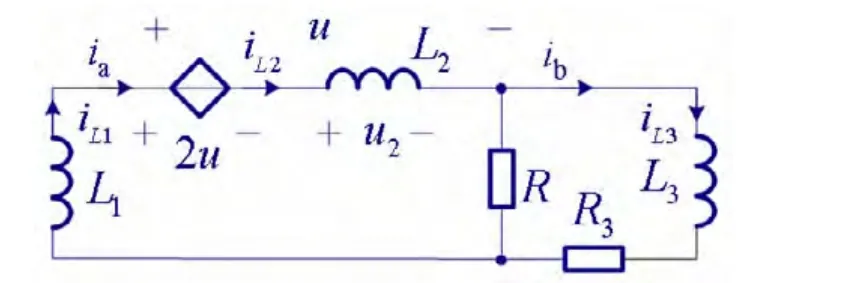
图3 动态电路之三
由图3所示电路可画出s域模型(这里从略),有网孔方程

其中,iL1(0-)=iL2(0-),且u=2u+u2或u=-u2=-L2diL2/dt,所以
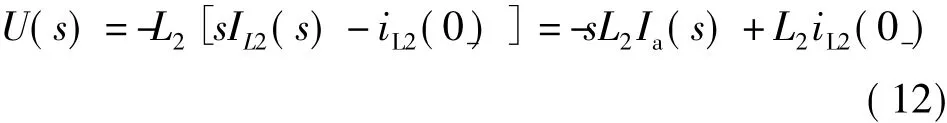
将上式代入式(11),经整理得
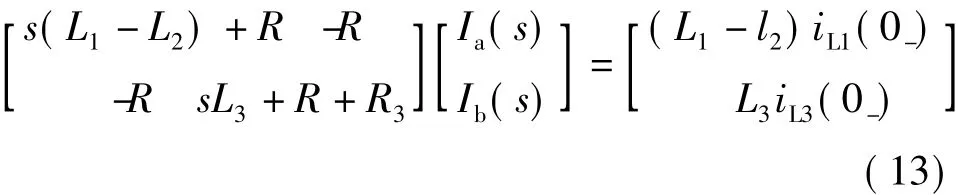
由上式解得
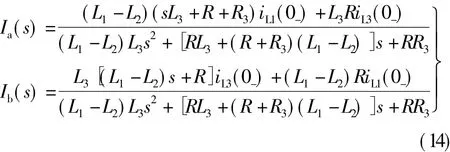
由上式可见,如果L1≠L2,则电路有两个固有频率,说明图3电路是一个二阶电路;如果L1=L2,则只有一个固有频率,此时Ia(s)=Ib(s),于是iL1=iL2=iL3,三个电感电流只有一个是独立的,说明图3电路是一个一阶电路。
3 进一步的讨论
电路的特性决定电路的拓扑约束和元件约束。因此,动态电路的阶数也决定于电路的拓扑约束和元件约束。在确定电路的阶数时,还应注意以下几个方面。
(1)零固有频率对电路阶数的影响。当电路存在零固有频率时,则该电路的零输入响应中就包含常数项[4]。因此,电路的零固有频率不影响电路的阶数。例如,对于如图4所示的电路,从输入端口看进去的网络函数(阻抗)为

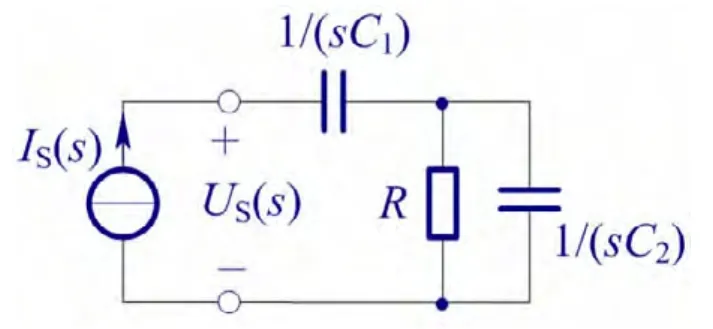
图4 动态电路之四
显然该电路存在一个零固有频率和一个非零固有频率s=-1/(RC2)。而该电路为一阶电路,说明电路的零固有频率不影响电路的阶数。
(2)电路的阶数与激励的关系。电路的激励包括电压源和电流源,作为电路元件,它们也会对电路起到拓扑约束(激励的接入方式)和元件约束(激励的电压电流关系)作用。从图2电路的分析可以看出,尽管电路的阶数与激励的大小无关,但与激励的形式(是电压源还是电流源)有关。
4 结语
本文通过电路实例讨论了电路的阶数确定方法,尽管现行教材对电路的阶数给出大致相同的定义,但这些定义具有一定的不确定性。事实上,只有当电路中的所有电路变量的微分方程的阶数都相同时,这些定义才是适用的。
本文的讨论可供教师在进行动态电路时域分析教学时参考。
[1] C.A.狄苏尔,葛守仁著,林争辉主译.电路基本理论[M].下册.北京:人民教育出版社,1979
[2] 于歆杰,朱桂萍,陆文娟.电路原理[M].北京:清华大学出版社,2007
[3] 陈希有.电路理论基础[M],第二版.北京:高等教育出版社,2004
[4] 陈洪亮,张峰,田社平.电路基础[M].北京:高等教育出版社.2007
[5] 徐贤敏.确定电路的阶时间常数和固有响应的零输入法[J].兰州:兰州铁道学院学报,1996,15(1):41-44

