总温总压测头模态振型变化规律研究
陈 钊,付 饶
(中国飞行试验研究院,陕西 西安 710089)
0 引言
采用测量耙测量航空发动机总温总压是发动机定型试飞中的主要测量手段之一[1],发动机试验时在相关气流流通壁面上安装温度和压力测量耙或测头,如果测量耙或测头的响应频率与发动机的振动或气流激励频率相吻合,会产生谐共振,使测量耙或测头容易损伤甚至断裂[2]。轻者测量耙或测头不能正常工作,重者将损伤发动机转动部件,危及飞机飞行安全。为确保测量耙或测头工作安全,在设计试验时除对其进行静强度校核计算外,还必须进行模态分析计算[3]。
1 理论分析
由于测头结构模型比较复杂,必须对模型进行简化后再进行理论分析,将测头简化为悬臂梁进行理论分析,悬臂梁结构简化如图1所示。

图1 悬臂梁示意图
设梁的长度为L,单位长度质量为ρ,抗弯刚度为EI,建立如图1所示坐标系,水平方向为x方向,垂直方向为y方向,在任意瞬时t,某一微元段的Y向位移可以用y(x,t)表示,根据其受力情况,微元段Y向位移运动方程为:

忽略转动惯量影响,各力对任一微元体的右截面上任一点的力矩之和应为0,即:

根据材料力学,弯矩与挠度曲线的关系为:

将公式(2)和公式(3)代入公式(1)得:
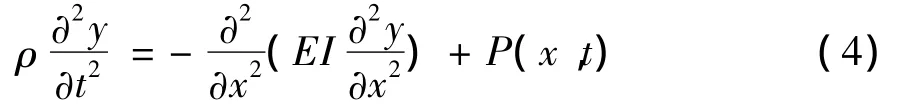
对偏微分方程(4)进行求解,得到表1结果。

表1 悬臂梁前5阶特征根
其中对于i≥3的各特征根可足够准确的取为:
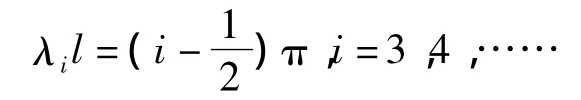
悬臂梁的各阶固有频率相应为[4]:
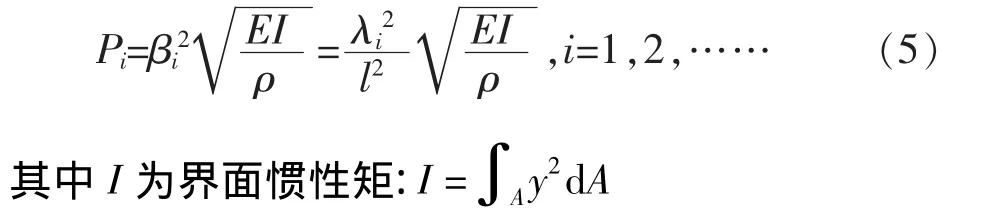
从公式(5)可以看出,对一固定材料的悬臂梁,其固有频率主要取决于长度和横截面惯性矩,对于总温总压测头,其结构虽然与悬臂梁相似,但是还是有很大区别,如图2所示,其各个截面根据长度不同是变化的,而且在孔的侧面开有测量孔,这些都会影响到测头的固有频率。因此仅依据公式计算,只能得出大概变化趋势,很难准确的计算出测头的固有频率以及得出测头固有频率随各个参数变化的曲线规律。为此,本文提出采用Ansys计算软件进行参数化建模,得到测头固有频率和变化曲线规律。
2 方法介绍
测头结构设计示意图如图2所示,在满足安装尺寸的情况下,这些尺寸的确定都将直接影响测头的固有频率,为了更好的确定测头的设计尺寸,本文采用Ansys计算软件进行参数化建模[5-7],然后分别修改不同的参数,得到各个结构尺寸下的计算结果[8],Ansys建立模型如图3所示,网格划分结果如图4所示。
在完成参数化建模和分网以后,不停改变相应参数进行模态分析,即可得到测头固有频率随相关参数的变化规律。
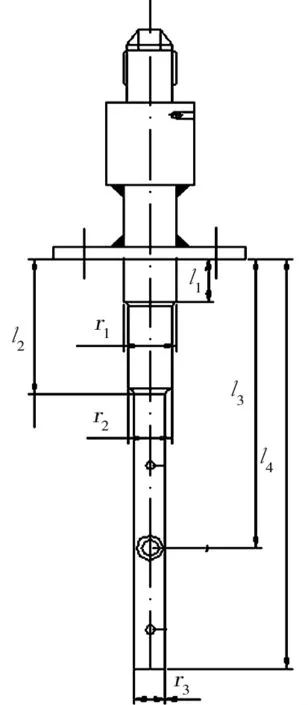
图2 结构示意图
图3 测头模型

图4 测头网格划分结果
3 计算结果与分析
如图5至图20为改变测头的8个尺寸参数得到的测头前四阶固有频率随这8个参数的变化规律曲线图。

图5 测头一阶二阶固有频率随r1变化曲线图

图6 测头三阶四阶固有频率随r1变化曲线图
图5图6为测头前四阶固有频率随r1变化曲线图,从两幅图可以看出:
a)测头前两阶固有频率随直径增大而增大;
b)其增速在逐渐变缓,其一阶固有频率在5.5到6变化时,半径每变化0.1 mm,固有频率增加约7 Hz,当直径从6.2增大到6.6时,半径每增加0.1 mm,固有频率只能增加5 Hz左右;
c)测头的三四阶固有频率的增加则基本随r1半径增加线性增加,增幅没有太大变化。
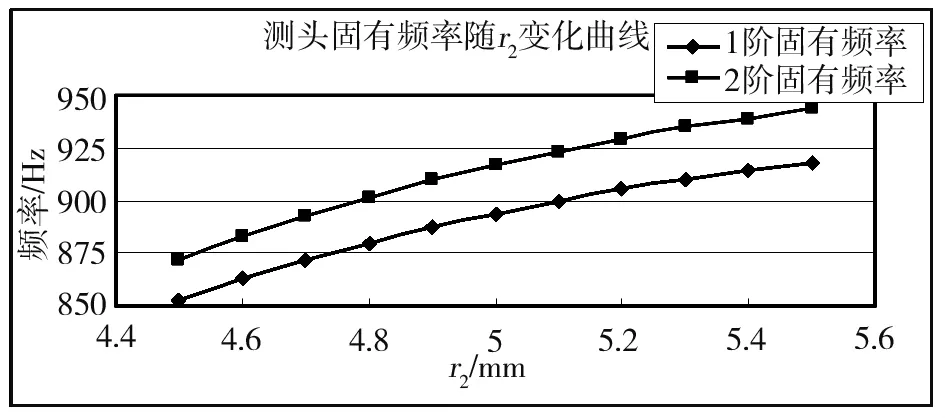
图7 测头一阶二阶固有频率随r2变化曲线图
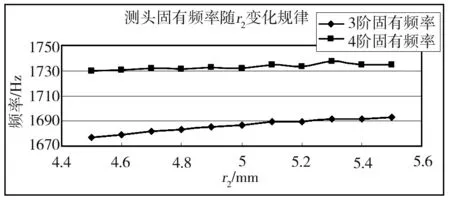
图8 测头三阶四阶固有频率随r2变化曲线图
图7图8为测头前四阶固有频率随r2变化曲线图,从两幅图可以看出:
a)测头前两阶固有频率随直径增大而增大;
b)其增速也是随着r2尺寸的增大而逐渐放缓;
c)测头的三四阶固有频率的增加则基本随r2半径增加变化非常小。

图9 测头一阶二阶固有频率随r3变化曲线图
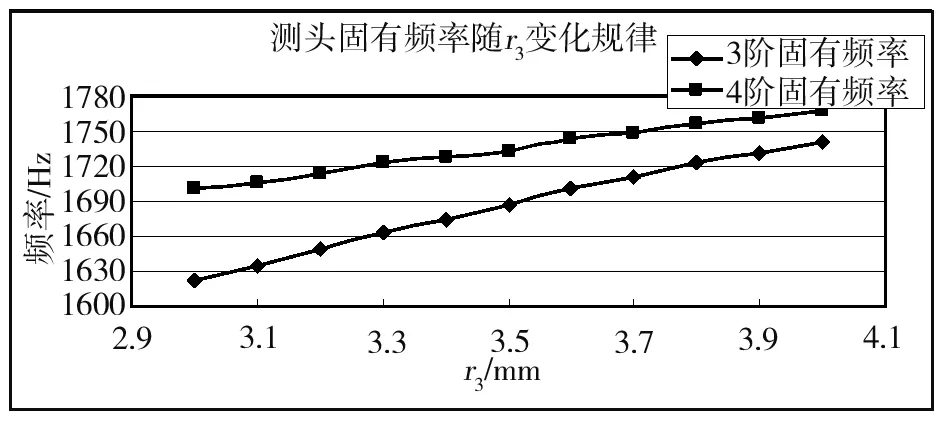
图10 测头三阶四阶固有频率随r3变化曲线图
图9图10为测头前四阶固有频率随半径r3变化规律曲线图,从这两幅图可以看出:
a)测头的前两阶固有频率并不是和r1,r2一样随着半径增大而增大,而是随着半径r3的增大先增大后减小;
b)测头的三四阶固有频率和r1,r2变化规律类似,是随着r3的增大而增大,其增幅也在随着r3增大而降低。
图11和图12为测头前四阶固有频率随孔内径r4变化规律曲线图,从这两幅图可以看出:
a)测头的前两阶固有频率与r3变化规律类似,是随着半径r4的增大先增大后减小,但其变化规律也有与r3不同的地方,其固有频率开始下降后,其下降幅度远远大于测头固有频率随r3增大而下降的幅度;
b)与前面所有参数变化规律不同的是,测头的三四阶固有频率是呈现出一个下降趋势,是随着r4的增大而逐渐下降的。

图11 测头一阶二阶固有频率随r4变化曲线图
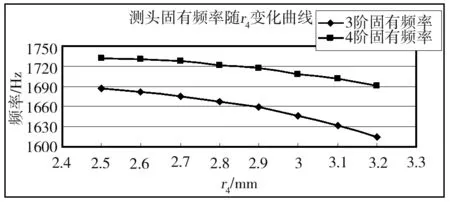
图12 测头三阶四阶固有频率随r4变化曲线图
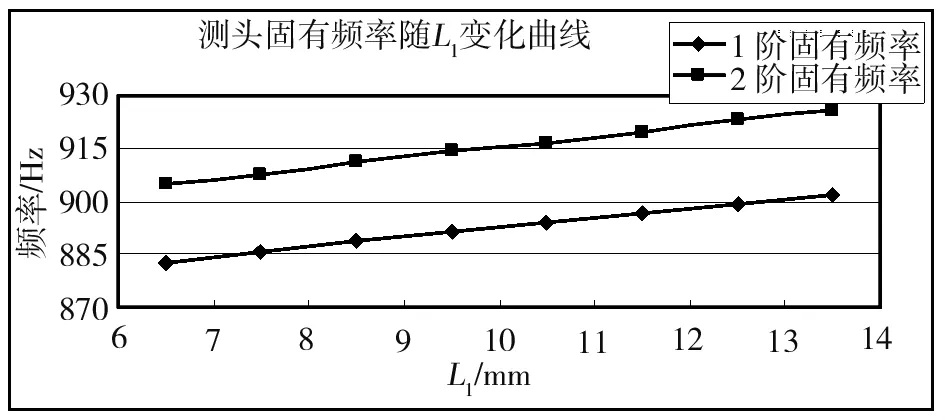
图13 测头一阶二阶固有频率随L1变化曲线图
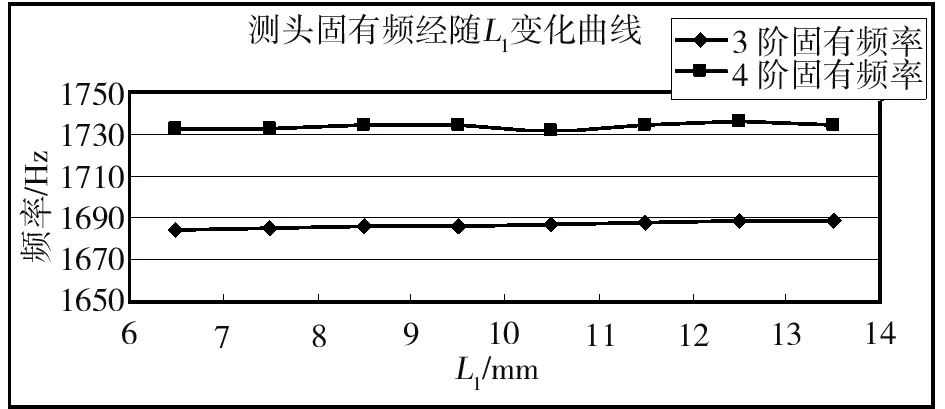
图14 测头三阶四阶固有频率随L1变化曲线图
图13和图14为测头前四阶固有频率随长度L1变化规律曲线图,从这两幅图可以看出:
a)测头一二阶固有频率随着L1增大而增大,但其变化幅度与r变化相比小了很多;
b)测头三四阶固有频率也是随着L1增大而增大,但其增幅与一二阶固有频率相比更小。
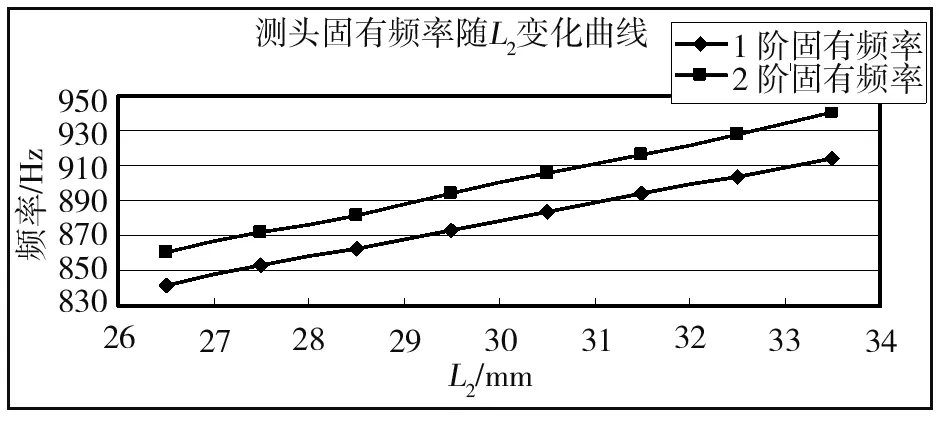
图15 测头一阶二阶固有频率随L2变化曲线图
图16 测头三阶四阶固有频率随L2变化曲线图
图15和图16为测头前四阶固有频率随长度L2变化规律曲线图,从这两幅图可以看出:
a)测头固有频率也是随着长度L2增加而增加,但其增大幅度比随L1变化幅度略大一些;
b)测头三阶固有频率随着L2增大也在增大,但其增大幅度已经明显小于前两阶的变化幅度,四阶固有频率随L2尺寸变化的变化幅度则非常小。
图17和图18为测头前四阶固有频率随长度L3变化规律曲线图,从这两幅图可以看出:
a)测头一阶固有频率随L3变化相对不大,二阶固有频率相对来说变化稍大一些;
b)测头的三四阶固有频率基本不变,不随L3长度变化而变化。
根据图17,L3表示测头上的开孔距离固定板的距离,计算结果可以看出,开孔位置只对测头的二阶固有频率有一定的影响,对其他前三阶固有频率影响不大。

图17 测头三阶四阶固有频率随L3变化曲线图

图18 测头三阶四阶固有频率随L3变化曲线图
图19和图12为测头前四阶固有频率随长度L4变化规律曲线图,从这两幅图可以看出:
a)与前几个长度参数不同,测头的前两阶固有频率是随长度L4的增大而降低的,而且其降低幅度相对前几个参数的增大幅度而言大了很多;
b)测头的三四阶固有频率也是随着长度L4的增大而降低的,但其降低幅度远小于测头的前两阶固有频率降低幅度。
图19 测头一阶二阶固有频率随L4变化曲线图
图20 测头三阶四阶固有频率随L4变化曲线图
4 总结
从对测头前四阶固有频率随8个参数变化规律曲线来看,可以得出如下结论:
a)测头的几个半径参数对测头的固有频率影响远大于几个长度参数对测头固有频率的影响,半径参数变化0.1 mm可以使测头的前两阶固有频率变化达到10 Hz以上,而长度参数至少需要变化1 mm才能达到接近这样的效果,所以当我们需要通过改变测头尺寸来改变测头固有频率时,改变半径参数的效果要远好于改变长度参数;
b)测头的固有频率随不同部位的尺寸变化是不同的,有些是递增的,有些是递减的,有些则是先增大后减小的,具体变化规律,必须通过计算才可以得到;
c)测头的三四阶固有频率的变化幅度普遍低于前两阶固有频率随同一参数变化的幅度。
得到测头固有频率随8个参数变化的规律曲线后,可以根据这8个规律曲线选择合适的参数来规避发动机所本身具有的激励频率,防止测头在实际试验中可能振断,造成对飞行安全产生的威胁。
[1] Yuhas A J,Ray R J,Burley R R,et al.Design and development of an F/A-18 inlet distortion rake:a cost and time saving Solution[R].NASA TM-4722
[2] 陶冶.基于ANSYS的航空发动机测量耙模态分析法.机械研究与应用,2013年第2期
[3] Amin N F,Hollweger D J.F/A-18A inlet/engine compatibility flight test results[R].AIAA 81-1393,1981
[4] 方同.振动理论及应用.1998
[5] 王新敏.ANSYS工程结构数值分析.人民交通出版社,2007-01
[6] 莫江涛,刘舜尧,王静文.用VisualC++与ANSYS实现螺旋结构参数化建模[J].机械设计与制造,2005年07期
[7] 刘洁,张和平,王丽娟.基于Visual C++的ANSYS参数化设计[J].机电工程技术,2003年05期
[8] 张洪才,何波.有限元分析ANSYS 13.0从入门到实战[M].北京:机械工业出版社,2011

