关于无穷小阶数的几点注记
杨吉英, 张 娟, 蔡姗姗
(1.保山学院 数学学院,云南 保山678000; 2.昆明理工大学 津桥学院工学系,昆明650106;3.普洱学院 数学与统计学院,云南 普洱665000)
1 引 言
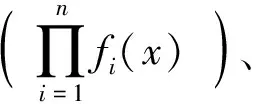
本文结合无穷小阶数的定义,给出阶数的相关运算性质以及确定阶数的常用方法,其中无穷小阶数的几条运算性质,解释了无穷小内容的两个难点:在什么条件下,两个无穷小可以进行阶的比较?在等价无穷小代换求极限中,在什么条件下相减和相加的因子能看成一个整体直接代换?
2 主要结论
在文献[10]中给出如下无穷小的阶数的定义.
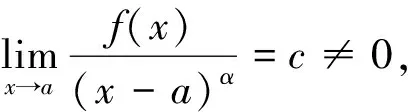
注1 并不是任一无穷小都有确定的阶数,即使与一切幂(x-a)α都能比较的.


注2f(x)是x→a时的α阶无穷小等价于f(x)与(x-a)α是同阶无穷小.

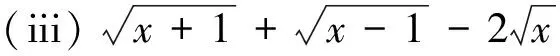


下面给出无穷小的阶数的一些运算性质.这些性质可以来解释初学者在学无穷小内容时比较困惑的两个问题:
(i) 是否任意两个无穷小都可以进行阶的比较?若不是,那在什么条件下两个无穷小才可以进行比较?
(ii) 在用等价无穷小代换求极限中,什么条件下相减和相加的因子能看成一个整体直接代换?如何代换?
引理1设x→a, or(f(x))=α, 则存在某一非零实数c,使得f(x)~c(x-a)α.
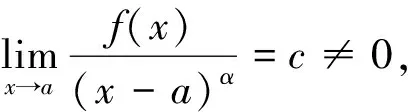
定理2设x→a, or(f(x))=α, or(g(x))=β,则f(x)与g(x)在x→a是同阶无穷小或高阶无穷小或低阶无穷小.


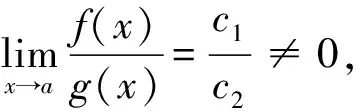


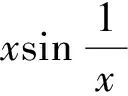
定理3设x→a, or(f(x))=α, or(g(x))=β,则有
(i) 若α<β,则or(f(x)±g(x))=or(f(x));

(iii) 若α>β,则or(f(x)±g(x))=or(g(x)).

故当α<β时,or(f(x)±g(x))=or(f(x));
(ii) ,(iii)同理得证.
此定理可以推广到有限个阶数存在且不相等的无穷小代数和情形,即有限个阶数存在且不相等的无穷小代数和的阶数取决于其中阶数最小的那个无穷小.
在满足定理3(i)的条件下,有

也就是f(x)±g(x)~f(x).从而可得到如下定理.
定理4设x→a, or(f(x))=α, or(g(x))=β,有
(i) 若α<β,则[f(x)±g(x)]~f(x);
(ii) 若α=β,f(x)~c1(x-a)α,g(x)~c2(x-a)α且c1≠∓c2,则
[f(x)±g(x)]~(c1±c2)(x-a)α;
(iii) 若α>β,则[f(x)±g(x)]~g(x).


解由于当x→0时,or(1-cosx)=2, or(sinx)=1,由定理4有
(1-cosx-sinx)~sinx,
故
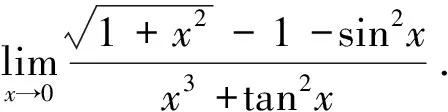

(x3+tan2x)~tan2x~x2,
故
若在限运算中,要把相加相减因子看成一个整体用等价无穷小代换,那确定无穷小的阶数变得尤为重要,下面给出常用的求无穷小阶数的方法.
根据无穷小阶数的定义,确定无穷小f(x)(x→a)的阶数主要取决于其等价无穷小中(x-a)α的幂α.

定理6设x→a, or(f(x))=α, or(g(x))=β,则有
(i) or(f(x)·g(x))=or(f(x))+or(g(x))=α+β;

(iii) 对任意非零实数k, or(kf(x))=or(f(x)).


即or(f(x)·g(x))=α+β=or(f(x))+or(g(x));
(ii),(iii)同理可证.
定理3给出的是两个阶数存在的无穷小相加相减后的阶数,而通过定理6可以确定两个阶数存在的无穷小相乘相除后的阶数.
定理7设函数f(x),g(x)在0的某个邻域上有定义,且有直到n阶导数,若f(x)-g(x)是x→0时的无穷小,且f(x)-g(x)的带有penao型余项的Taylor展开式为
f(x)-g(x)=ckxk+o(xk) (ck≠0),
则or(f(x)-g(x))=k.
证由题意有f(x)-g(x)=ckxk+o(xk)(ck≠0),故
且ck≠0,由无穷小阶的定义可得结论成立.
定理7告诉如何求阶数存在的两个等价无穷小做差后的阶数,是定理4(ii)的补充.借助定理7和定理4(ii),可以把等价无穷小代换中相加相减项等价代换做进一步的推广.
例4分别求当x→0时,
(i) or(ln(1+3x3)); (ii) or(sin2x(ex-1))=3; (iii) or(tanx-sinx).

(ii) 当x→0时,or(ex-1)=1, or(sin2x)=2,由定理6(i)有,or(sin2x(ex-1))=3,也就是sin2x(ex-1)~x3;
(iii) tanx,sinx在x=0处带有penao型余项的Taylor展开式分别为
由定理7有or(tanx-sinx)=3.
3 结 论
本文给出了无穷小阶数的若干注记,并从无穷小阶数的角度去统一解释,并不是任意的两个无穷小都可以比较,阶数都存在时,就可以做阶的比较.以及用等价无穷小代换求极限中,相加相减因子不能直接代换,但在保持代换后整体阶数不变的前提下,可以根据阶数的大小来进行等价代换.最后给出可以通过等价无穷小、无穷小阶数的运算性质、Taylor公式来确定无穷小的阶数的常用方法.
致谢非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

