问题与征解
2021-10-30 09:01:24
大学数学 2021年5期
注:读者在提供问题解答时, 请先提供印刷体的版本, 并注明单位、姓名和身份(教师、本科生或研究生等). 解答被选用后需提供word版本.
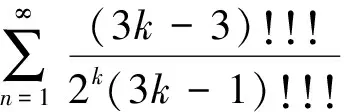
问题8(供题者: 浙江大学王梦) 对于x=(x1,x2,…,xn)∈n,定义以及现设A∈n×n以及M>0满足:∀x∈n成立‖Ax‖∞≤‖x‖∞以及‖Ax‖1≤M‖x‖1.证明:对于任何1≤p<+∞,存在仅与M,p有关(与n无关的)常数Mp使得∀x∈n,成立‖Ax‖p≤M‖x‖p.
问题1解答

以下解答由崔世勋(复旦大学数学科学学院2018级本科生)提供. 给出本题正确解答的还有国防科技大学陈挚.
1 回 顾
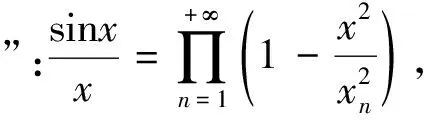
尽管最后结果是正确的,当时Euler给出的过程是不严谨的.现在我们借由复变函数的知识,参考Euler的这一想法解决此问题.
2 解 答
记g(z)=2020sinz-2021zcosz,这是一个整函数,并且是奇函数.证明将分为三步进行.
2.1 g(z)只有实零点
设z=x+iy是g的零点,其中x,y∈.则计算可得g(z)=0等价于:因此实部与虚部成比例.如果x,y均不为0,则有严格小于严格大于2,因此等号不可能成立.而若y=0,这就表明z是实数;而若x=0,g(z)=0就变为此方程只有零解.因此断言2.1成立.
2.2 应用Hadamard分解定理
这一核心步骤运用了复变函数的相关知识,见文献 [1] 的第五章.相关定义摘录如下:
增长阶设f(z)是整函数,若存在正数ρ与常数A,B>0使得|f(z)|≤AeB|z|ρ,∀z∈,则称f(z)有≤ρ的增长阶.而f(z)的增长阶定义为满足上式的所有ρ的下确界.
典范因子对非负整数k,定义典范因子为E0(z)=1-z,Ek(z)=(1-z)ez+z2/2+…+zk/k,∀k≥1.
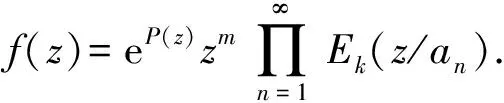
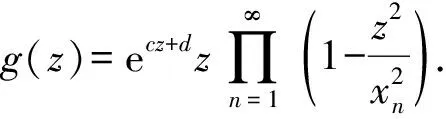
2.3 结果
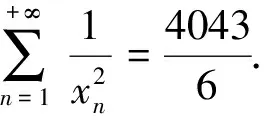
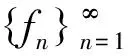
猜你喜欢
中国核电(2021年3期)2021-08-13 08:55:58
美与时代·美术学刊(2020年7期)2020-10-13 12:24:04
校园英语·月末(2020年4期)2020-06-08 12:54:41
数理化解题研究(2020年13期)2020-05-07 03:29:02
数学物理学报(2019年5期)2019-11-29 07:46:30
数学年刊A辑(中文版)(2019年1期)2019-01-31 02:35:22
下一代英才(酷炫少年)(2017年6期)2017-06-28 11:37:49
高中生·天天向上(2016年9期)2016-11-22 09:10:34
中学生天地(C版)(2016年4期)2016-09-16 03:19:02
党史文苑(2016年11期)2016-09-10 07:22:44

