基于贡献因子的改进决策树属性选择方法
郑 麟
(汕头职业技术学院计算机系,广东 汕头 515000)
0 引言
1 ID3算法的属性选择方法
1.1 ID3算法的基本思想
ID3算法用信息增益(熵)作为属性的选择标准,即选择具有最高信息增益(或最大熵压缩)的属性作为当前结点的测试属性,该属性使得结果划分中的样本分类所需的信息量最小.具体方法是:检测所有的属性,选择信息增益最大的属性产生决策树结点,由该属性的不同取值建立分支(称为分枝优选),再对各分支的子集递归调用该方法建立


其中pi是任意样本属于Ti类的概率,即pi=si/s.因为信息是用二进位编码的,所以对数函数以2为底.如果以属性A作为第一个决策树划分属性,设属性A有v个不同的值{v1,v2,…,vv},可以将S划分为v个子集{S1,S2,…,Sv},用Sj表示,Sj中的样本在属性A上具有相同的值aj(j=1,2,…,v),对于给定子集Sj的期望信息由下式给出:

公式(2)实际上是由公式(1)而来,只不过将整个样本集S换成样本子集Sj,两者的区别在公式(2)只需要计算属性A的值等于aj的样本子集Sj的熵,而公式(1)用来计算整个样本S的总期望信息(即总熵).由此可知Pij=sij/sj,其中sij是子集Sj中属于类Ti的样本数.所以样本子集Sj中的样本总数为s1j+s2j+…+snj,在计算由属性A划分后的总熵时我们必须在每个样本子集Sj的熵前面乘上权值(s1j+s2j+…+snj)/s,其中s是样本集S的总样本数,即用属性A作为决策树第一个划分结点得到的熵为:
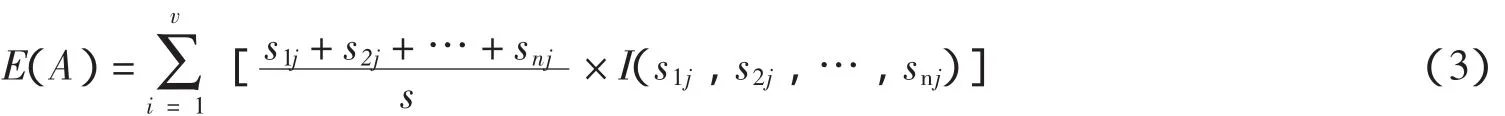
因此,划分后的信息增益为原来的总熵减去划分后的总熵即:

熵值E(A)越小,子集划分的纯度越高,因此算法选取具有最高信息增益的属性作为给定集合S的测试属性,创建一个结点,并以该属性标记,对该属性的每个值创建一个分支,并据此划分样本,如此反复不断构造决策树的下一级直至所有的样本子集只有一个类别,这时表明系统的熵为零,决策树构造过程完毕[5].
1.2 ID3属性选择的性能分析
ID3算法的属性选择方法简单、基础理论清晰,能够快速和高效的构造出平均深度较小的决策树,但是该算法存在着一些缺陷[7]:首先,ID3算法在选择信息增益作为分裂属性的选择标准时,偏向于优先选择取值较多的属性,而取值较多的属性往往不是最优的属性,这在实际应用中往往不太合理;其次,ID3算法对噪声较为敏感,当训练样本集变动时,决策树会随之大幅度变化,不利于渐进学习.最后,该方法没有考虑属性间的相关性,不能处理属性值缺省的情况,也不能处理连续型属性.
已经提出的C4.5算法能较好的解决不能处理连续属性的问题,而对于其他缺陷,许多学者提出各种各样的解决方法:针对属性间的相关性问题,文献[8]引进属性依赖度来改进算法性能;针对优先选择取值较多属性的缺陷,文献[9]提出一种基于属性贡献度的决策树算法,从属性选优上消除了多值属性选择的偏向;文献[10]则提出一种合理且可靠的MID3改进算法,在一定程度上解决多值偏向问题;文献[11-12]引入属性重要性和属性取值数量2个参数对ID3算法的信息增益公式进行改进,并根据凸函数的性质简化信息熵的计算,提高决策树的构造效率;文献[7]使用泰勒公式和麦克劳林公式提出了新的属性选择标准,改进后的算法通过简化信息熵的计算,提高了分类准确度.由以上研究成果可知,许多研究者主要针对该算法优先选择取值较多属性的缺陷,对属性选择标准进行改良,本文在参考以上研究成果的基础上,结合实际研究工作,在只对离散型属性进行划分的前提下,提出属性贡献因子的概念并将其作为ID3算法属性选择的重要参考依据,并对ID3属性选择方法在数学上进行适当的等价变换使其简化,最后达到提高属性分类精度和速度的目的.
2 信息熵的简化与优化
2.1 信息熵的近似变换
将公式(1)、(2)、(3)带入到公式(4)可得信息增益的公式为:
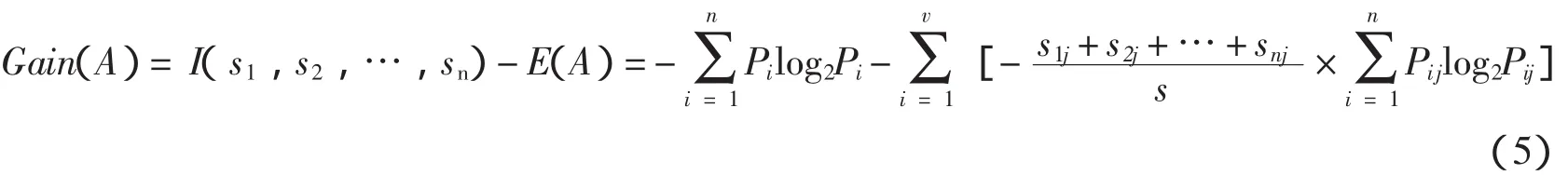
对于I(s1,s2,…,sn)的部分,只要给定了训练样本和类别数,pi就是不变的,因此它在整个决策树构造中始终为定值,可以把它从公式(5)中去掉,只保留E(A)来考虑如何改进算法.在E(A)中要进行多次的对数计算,由文献[13]可知log x函数在[0,1]上是凸函数,Pij取值在[0,1]上,所以可以运用凸函数的性质.
性质1[13]设f(x)为凸函数,X为非空集合,则由可推出
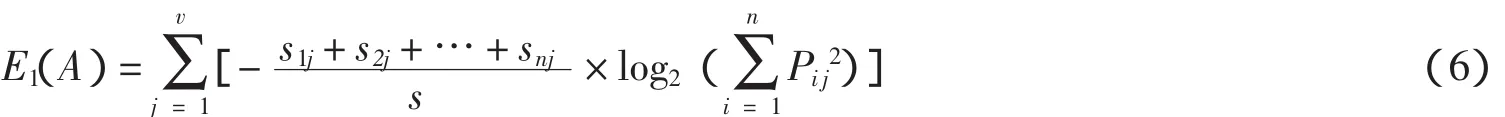
公式(6)是计算信息增益的简化公式,由此完成了属性选择标准改进的第一步.
2.2 属性信息熵的优化
ID3属性选择标准的主要缺陷是算法优先选择取值较多的属性,因此应着重在这方面进行改良,已有的C4.5算法是通过信息增益率作为属性选择标准,但是很明显的这会阻碍选择属性值分布均匀的属性,即偏袒取值较少的属性,而较好的解决方法是即不偏袒取值较多的属性,也不偏袒取值较少的属性.本文提出了一种基于贡献因子的属性选择标准.主要思想是:首先根据公式(5)的属性选择标准计算出各个特征属性的信息增益,从而选择出信息增益最大(即信息熵E(A)最小)的属性记为属性A1,然后计算出属性取值个数最多的属性A2,如果A1≠A2,说明信息增益最大的属性不是取值个数最多的属性,选择该属性作为测试属性不会产生多值偏向问题;如果A1=A2,则说明信息增益最大和取值个数最多的属性为同一属性,用它作为测试属性易产生多值偏向问题,应对该属性的信息增益用贡献因子来修正,以避免取值异常偏向.在用属性A划分时加入贡献因子(用函数Contribute(A)表示)修正其信息增益,则得到公式(7):
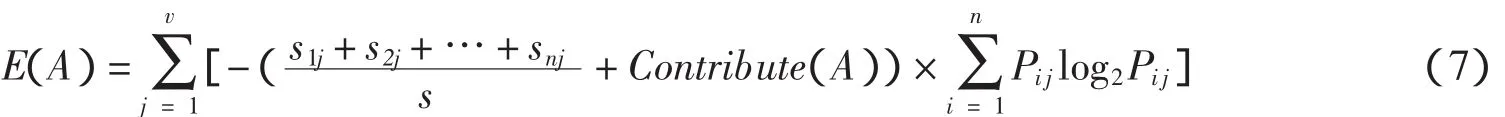

由上面的讨论可以得到贡献因子Contribute(A)的表达式如下:

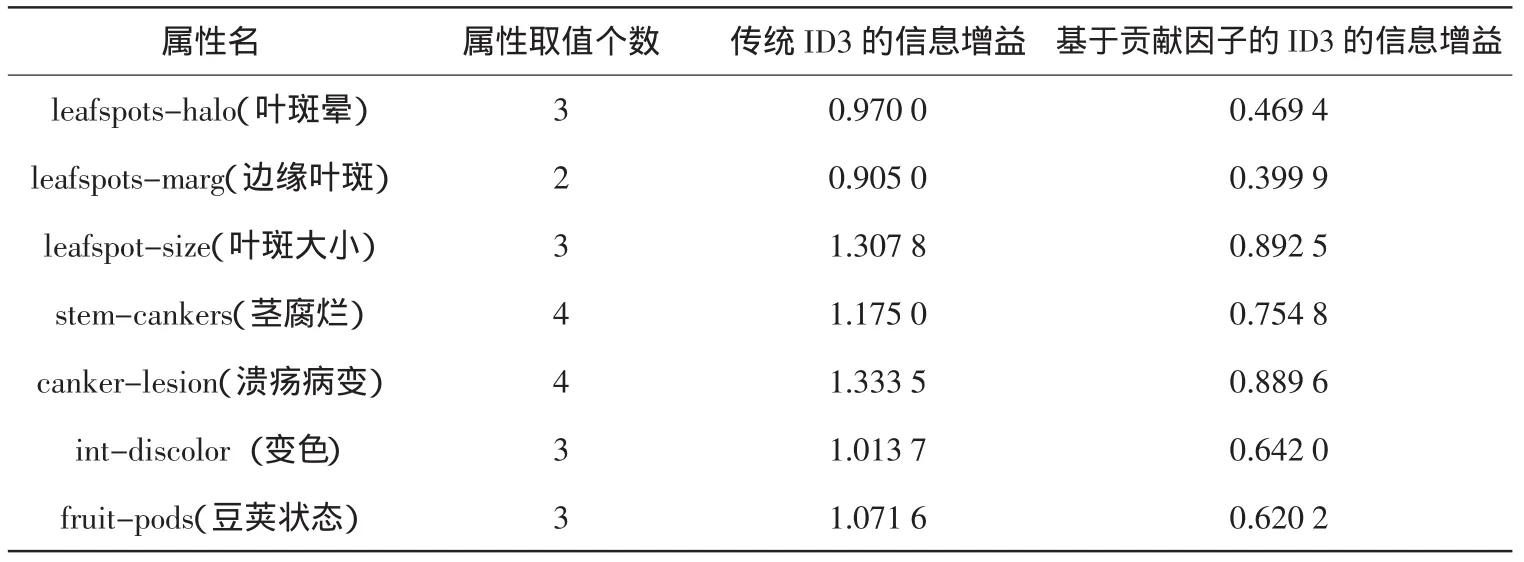
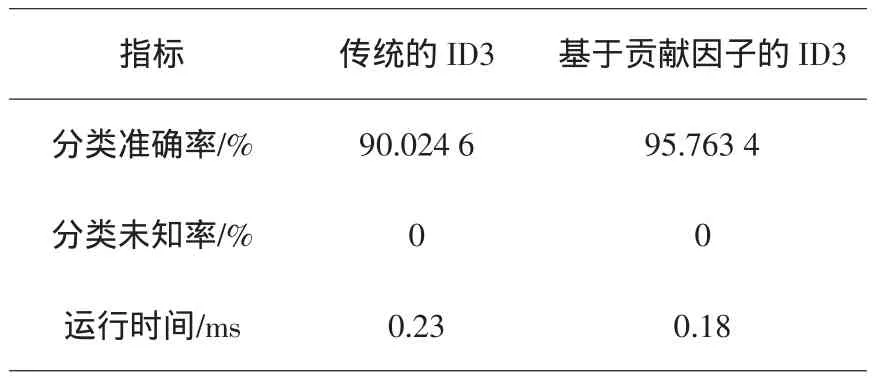
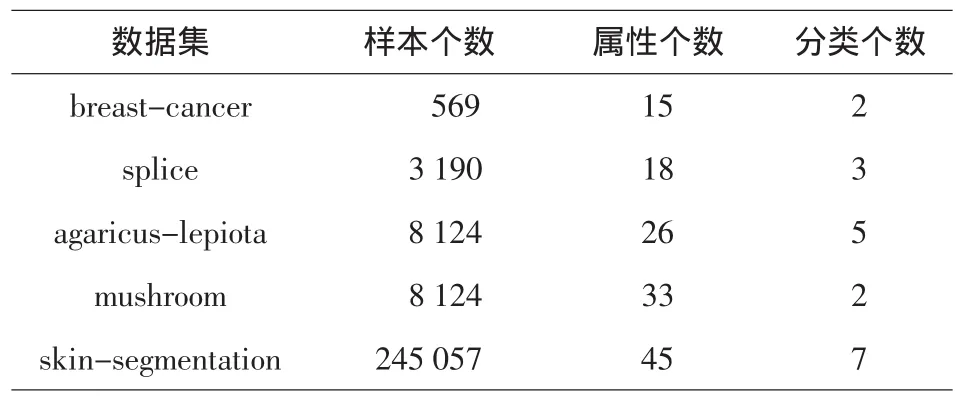
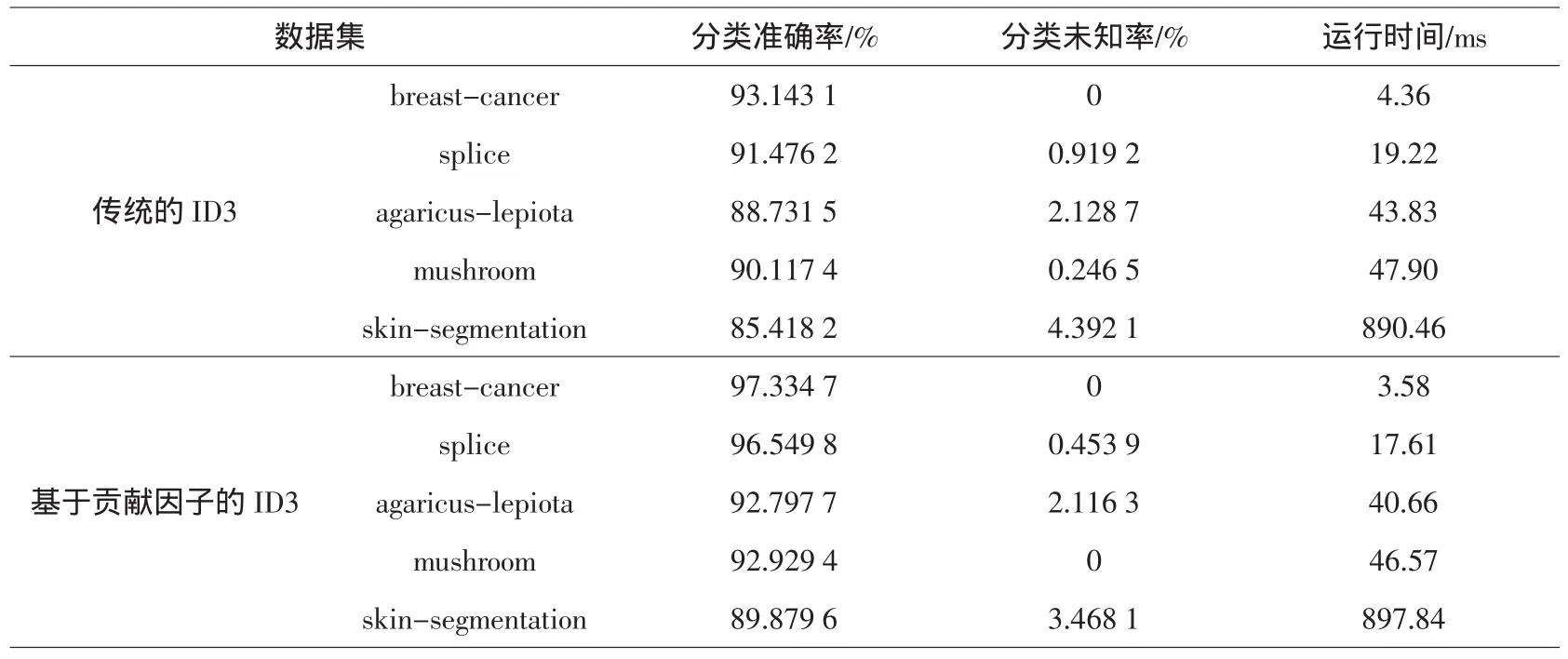
由于sgn(sij)≤sij 以上讨论了ID3属性选择标准的简化与优化,结合公式(6)、(7)、(8)和(9)可以得到属性A的信息增益E(A)的综合改进公式: 由公式(5)和公式(10)可以得到最后的信息增益计算公式: 可以使用公式(11)计算改进后的信息增益,达到简化计算和优化决策树划分的作用. 为说明基于贡献因子的ID3算法的优势,先进行小数据集测试以达到简化分析的目的.测试的数据集使用UCI经典数据集soybean中随机取出的30条记录,该数据集包括8个属性,最后一个是类属性class,前面7个属性用来预测soybean(大豆)病变的类型,分别运行了传统的ID3算法(使用公式(5))和基于贡献因子的ID3算法(使用公式(11))计算各个属性的信息增益,实验结果如表1所示. 表1 小数据集分析结果 由实验结果可知,用传统ID3算法计算出来的信息增益中,属性 canker-lesion(溃疡病变)的增益最大,但是其拥有的属性取值个数也最大,作为第一个划分结点值得商榷,在加入贡献因子之后,属性leafspot-size(叶斑大小)的信息增益变为最大,而其属性取值个数并不是最大的,很明 显取属性leafspot-size作为划分属性较为合理.从生物学角度来看,溃疡病变作为大豆病变的一种普遍症状,并不能对病变进行合理分类,而叶斑大小很大程度上是和病变的类型相关的,这也解释了使用leafspot-size作为划分属性的合理性.从分类准确率、未知率和运行时间方面来评估两种方法如表2所示. 从表2可以看出,改进后的ID3属性划分方法不仅在分类准确率上有所提高,而且由于简化了对数函数的计算,所以在运行时间上也有所改进. 表2 小数据集上的算法性能比较 为说明改进算法具有普适性,采用各种不同量级的UCI数据集对其进行测试,实验中选用样本个数和属性个数从小到大的数据集进行测试,各数据集的分布情况如表3所示. 表3 数据集的分布情况 在上面5个数据集上分别采用传统的ID3算法和基于贡献因子的ID3算法进行分类,结果如表4所示. 表4 不同量级数据集上的算法性能比较 由实验结果可知,基于贡献因子的ID3算法在不同量级的数据集下的分类准确率和分类未知率均优于传统的ID3算法.在中小量级的数据集中,改进的算法亦表现良好,运行时间较短;而在大型数据集中,改进的算法由于计算贡献因子的时间消耗增加,导致算法的总运行时间会比传统算法稍慢,但是从提高分类准确率的效果来看,这点时间消耗是值得的. 基于贡献因子的决策树属性选择方法对传统的ID3属性选择方法作了改进:首先简化了信息熵的计算复杂度,提高算法的运行速度;然后提出了贡献因子的概念,平衡了ID3算法的属性取值偏向,改善了分类结果.实验结果分析表明,对于相同的数据集,相较于传统的ID3算法,基于贡献因子的算法提高了决策树分类的准确率,缩短了运行时间.但是,属性的重要程度和属性取值个数之间还存在着复杂的关系,本文只是平衡了属性取值个数的问题,如何将重要程度和取值之间联系起来并考虑处理缺失值是今后研究的重点. [1]Tan P N,Steinbach M,Vipin K.Introduction to data mining[M].北京:机械工业出版社,2011. [2]Quinlan J R.Induction of decision trees[J].Machine Learning,1986,1(1):81-106. [3]董广,王兴起.基于决策分类熵的决策树构造算法及应用[J].计算机应用,2009,29(11):3103-3106. [4]陶荣,张永胜,杜宏保.基于粗集论中属性依赖度的ID3改进算法[J].河南科技大学学报:自然科学版,2010,31(1):42-45. [5]Quinlan J R.Simplifying decision trees[J].Internet Journal of Man-Machine Studies,1987,27(3):221-234. [6]Han J,Kamber M.数据挖掘:概念与技术[M].范明,孟小峰,译.2版.北京:机械工业出版社,2006. [7]谢妞妞,刘於勋.决策树属性选择标准的改进[J].计算机工程与应用,2010,46(34):115-118. [8]史岳鹏,朱颢东.基于类别相关性和优化的ID3特征选择[J].数据采集与处理,2011,26(2):230-234. [9]孙淮宁,胡学钢.一种基于属性贡献度的决策树学习算法[J].合肥工业大学学报:自然科学版,2009,32(8):1137-1141. [10]王永梅,胡学钢.基于用户兴趣度和MID3决策树改进方法[J].计算机工程与应用,2011,47(27):155-157. [11]张 琳,陈燕,李桃迎,等.决策树分类算法研究[J].计算机工程,2011,37(13):66-70. [12]朱颢东.ID3算法的改进和简化[J].上海交通大学学报,2010,44(7):883-886. [13]陈纪修,金路,於崇华.数学分析[M].北京:高等教育出版社,2004. [14]周海波.基于决策树的分类算法研究[D].兰州:兰州大学,2009.2.3 属性信息熵的综合改进
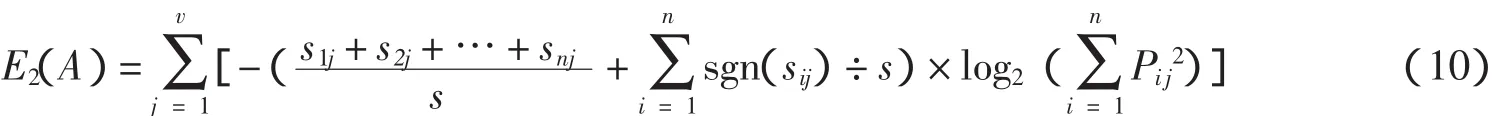

3 实验及结果分析
3.1 小数据集测试分析
3.2 不同量级的数据集测试分析
4 结束语

