有限反馈的MIMO系统容量分析

周 雯,王 军

(汕头大学电子工程系,广东 汕头 515063)

0 引言

多天线(Multiple-Input-Multiple-Output,MIMO)系统在接收机和发射机都采用了多根天线,可以有效地提高系统的数据传输速率,已经成为下一代无线通信系统的物理层调制规范[1-2].不同环境下的MIMO系统的容量问题是研究的热点问题之一[5-6].Telatar[3]和Foschini[4]在作出了收发天线间是独立不相关的衰落的假设下,首先推导出了多天线系统在高斯信道下的开环和闭环容量表达式.在文献[5]中,Li等人推导了多天线正交频分复用多址接入系统容量最大化的充分和必要条件,并且给出了在低信噪比区域、高信噪比区域等多种情况下的容量近似表达式.在文献[6]中,Qin等人研究了极化分集方式对于MIMO系统容量的影响.该研究发现在接收端和发送端采用不同的天线极化方式比采用单一的极化方式(即都采用圆极化或者都采用线极化方式),会显著提高系统的容量.

信道状态信息反馈对于发送端进行预编码设计、闭环功率控制等具有非常重要的意义.早期的文献一般假设发送端具有理想的信道信息,但是实际中反馈信道通常是有噪或者限速率的.在限速率的反馈信道下,有限反馈技术和多天线技术或者正交频分复用技术相结合,近来得到了广泛的关注[7-15].基于有限反馈的MIMO系统一般有两个研究方向:一是研究如何利用有限反馈提高系统的容量,如协方差量化反馈方法[7-8]和线性预编码方法[9-10,14],另一方向是侧重于如何利用有限反馈技术提高空时编码的误码率性能[11].文献[7]提出了在限速率反馈信道下一种功率控制和波束赋型混合的系统结构,并且发现所提出的混合结构逼近闭环的系统容量.天线选择是线性预编码方法的一种,基于天线选择和有限反馈方法,文献[10]提出了一种自适应的闭环功率控制方案,并且发现提出的方法比多模天线选择策略[12]有更高的吞吐率.

本文研究了单用户有限反馈下的闭环MIMO系统的容量问题.假设发送端和接收端均储存相同的码本集合,接收机具有理想的信道估计.接收机搜索码本集合的码本求出与之最匹配的信道矩阵,并且将索引值通过限速率的信道反馈给发送端.而发送端根据收到的索引查找相应的码本集合从而找出相应的矩阵,进行矩阵的奇异值分解和数据子流功率分配等操作,然后将处理后的数据发送出去.当反馈比特数较低时,反馈信道信息不准确可能不会产生相对于开环MIMO系统的容量增益,所以就存在反馈比特数的下限以确保闭环容量增益大于或者等于零.本文采用数值计算方法研究了反馈比特数对MIMO系统容量的影响,分别给出了在不同的系统配置下,采用RVQ[18]和LBG[13]码本生成方法对应的最小反馈比特数.

1 系统模型

图1描述了闭环MIMO系统模型,发送端和接收端的天线数目分别为NT和NR.发送端通过VBLAST编码(Vertical-Bell Laboratories Layered Space-Time,垂直分层空时编码)和数据子流功率分配操作,将用户数据x发

送出去.假设接收机具有理想的信道信息,它通过MMSE-SIC(Minimum Mean Square Error-Successive Interference Cancellation,最小均方误差-串行干扰抵消)数据检测算法得到检测的比特流.这种发射机和接收机的结构可以达到多天线高斯信道的容量.假设信道是平坦衰落的,则接收信号可以写为:

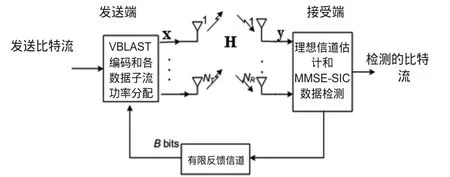
图1 闭环MIMO系统模型

其中:H是维度为NRXNT的的信道响应矩阵,y=[y1y2…yNR]T,(.)T代表转置操作;发送信号x=[x1x2…xNT]T,噪声w=[w1w2…wNT]T,并且其相关矩阵满足

上式中E(.)代表数学期望,INR是NRXNR的单位矩阵.发送端和接收端均保存相同的量化码本集合Ψ={φ1,φ2…φ2B},其中码本φi是NRXNT的矩阵,2B是码本总数目,而码本集合Ψ可以通过LBG算法[13]或者RVQ方法[18]构造.接收机得到理想的信道信息后将选择与之最匹配的码本矩阵,并且将索引通过有限反馈信道反馈给发送端,反馈的比特数是B.选择准则如下式所示:

其中||.||代表矩阵的Frobenius范数,这样得到的i*是所选最优集合φj的下标.最后,MIMO闭环系统的信噪比定义为

其中P是发送总功率,σ2w是高斯加性白噪声的方差,由式(2)给出.

2 闭环MIMO系统容量和反馈比特数下限

2.1 MIMO系统的开环容量

假设发送端不知道信道信息(Channel State Information,CSI),即不存在反馈信道反馈信道信息,则最优的功率分配是等功率分配方法.此时MIMO系统的开环容量为:

其中:SNR是MIMO系统的信噪比.当发送信号分布为复高斯分布并且发送端每个数据子流为等功率时系统可以达到上式(5)所示的开环容量.用矩阵的奇异值分解(Singular Value Decomposition,SVD),可以把开环容量进一步写成:

其中:Nmin=min(NT,NR),{λi}Nmini=1是矩阵HHH的奇异值.

2.2 有限反馈下的MIMO系统的闭环容量

在图1所示的闭环MIMO系统中,由于有限反馈的精度是有限的,量化误差导致反馈的信道信息存在失真,因此系统的容量相比理想的信道信息反馈存在差距.当发送端收到接收机反馈的索引i*后,将从码本集合Ψ选择相应的码本φi*,记H'=φi*

以表示失真的信道信息,然后用奇异值分解方法把H'分解为:

注意为表达方便该文把上式中矩阵∧写成对角阵的形式,即使它不是方阵(NR≠NT).接下来发送端采用特征模式传输方式,即对原始发送信号x采用如下线性变换:

其中V由表达式(7)获得,D是一个对角阵,其对角线元素为:

其中u满足

其中:λi是矩阵∧的第i个对角线元素,矩阵∧由式(7)给出并且可以进一步写成∧=diag因此相应的接收信号y由下式给出:

为求出闭环MIMO系统的容量,下面引入一个定理.

定理1[17]考虑如下MXN的多天线系统:

其中:h是NXM的复信道矩阵,S是MX1发送信号向量,V是NX1的加性噪声向量.假设发送信号和加性噪声的功率分别为M和N,并且噪声和发送信号不相关.令发送信号S的自相关矩阵为RS,接收信号Y的自相关矩阵为RY,则下式成立:

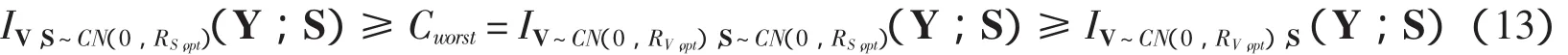
其中:I(Y;S)表示发送信号S和接收信号Y之间的互信息量,x~CN(0,RX)表示随机向量x服从均值为零、协方差矩阵为Rx的复高斯分布,而RV,opt和RS,opt是指满足下式的最优接收信号自相关矩阵和发送信号自相关矩阵:

式(13)表明:当发送信号分布确定,噪声为高斯分布的系统的互信息量最小;而当噪声信号分布确定时,发送信号为高斯分布时系统的互信息量最大.接下来继续推导系统的闭环容量,令Y=HVD1/2,则采用特征传输模式下的MIMO系统闭环容量C∧满足:

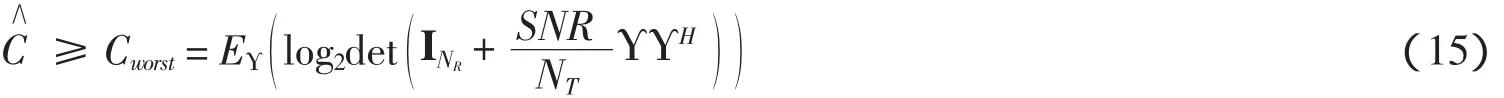
等号仅当噪声为高斯分布时成立.考虑到整个系统的等效噪声是w,与有限反馈信道无关;并且w是是高斯白噪声,所以式(15)的等号成立,于是我们就可以得到有限反馈下的闭环MIMO系统容量的表达式.系统的整个操作流程可以归纳为:

第一步:接收机通过信道估计得到理想的信道信息H,通过式(3)选择与之最匹配的码本矩阵,求出相应的索引,通过有限反馈信道传输给发送端.

第二步:发射机得到索引值,从码本集合Ψ选择对应的码本,然后采用式(7)表述的奇异值分解得到矩阵的特征向量V,然后通过式(9)和(10)描述的注水法得到矩阵D.

第三步:发射机采用式(8)描述的线性变换,把转换后的信号发送出去.

2.3 最小反馈比特数

当发送端具有理想的信道信息时,闭环MIMO系统容量大于开环系统的容量.但是当发送端获得的信道信息有失真时,非理想的信道信息可能会导致发送端采用不匹配的特征模式传输信号,如式(8)所示.当量化误差过大时,闭环系统的容量可能会小于对应的开环系统容量,所以存在反馈比特数的下限以确保闭环系统容量不小于开环系统的容量.将有限反馈的闭环系统容量写成C∧=C∧(NT,NR,SNR,B),其中SNR是系统的信噪比,B是反馈比特数.同样,将开环系统容量写成Copen=Copen(NT,NR,SNR).则系统所需的最小反馈比特数由下式给出:

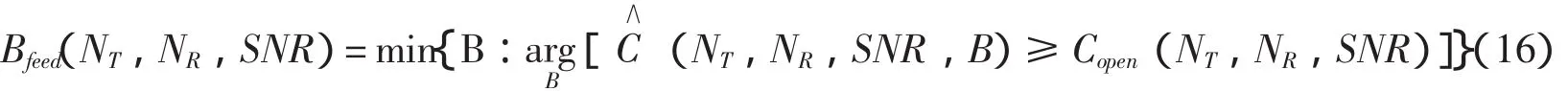
3 数值结果

此节采用数值仿真的方法研究了有限反馈下的MIMO系统容量.信道采用平坦瑞利衰落信道模型,因为工程中LBG[13]方法和RVQ方法[18]较为经典和常用,所以码本集合分别采用这两种算法构造,MIMO系统的开环容量采用式(5)计算,有限反馈的闭环容量采用式(15)计算.

3.1有限反馈下的闭环容量

图2绘制了采用不同精度码本的系统闭环容量与信噪比的关系.分别考虑了发送和接收天线对为(2,2)和(4,2)的两种情况,而码本采用LBG方法构造.可以看到,在某个固定的信噪比下系统容量随着码本比特数的增加而增加.采用较低精度码本的闭环容量可能小于开环容量.例如:对于2X2系统,当MIMO系统信噪比为8 dB并且码本比特数B=3或者5时,系统闭环容量小于开环容量.为保证有限反馈的闭环容量大于等于开环容量,在8 dB时,2X2的MIMO系统应该采用不小于7位的码本.

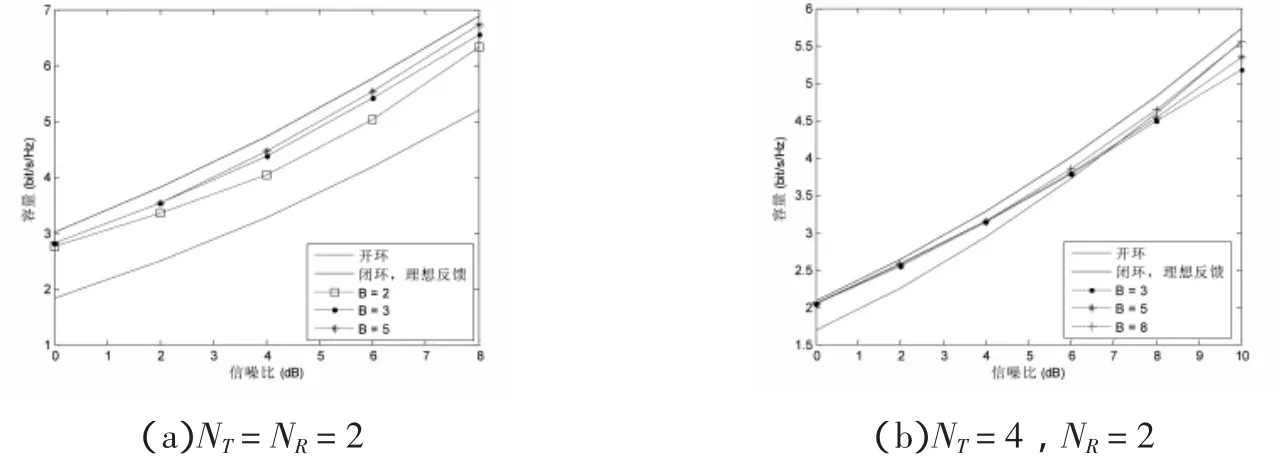
图2 采用不同精度码本的MIMO系统闭环容量与信噪比的关系

3.2 不同码本生成方式的性能对比

图3 对比了分别采用LBG码本和RVQ码本的系统闭环容量,分别考虑了发送和接收天线对为(2,2)和(3,3)的两种情况.可以看到,对于(2,2)系统,在信噪比为0 dB、4 dB、8 dB的时候,采用两种方法的系统性能无显著差别,而且对于码本比特数B∈[3,8]时,系统容量随着码本比特的增加几乎没有显著变化.但是对于(3,3)系统,情况发生了明显变化,采用RVQ码本要优于LBG码本.例如:在信噪比为4 dB并且均采用3比特码本时,采用RVQ码本会产生相对于LBG码本约0.33 bit/s/Hz的增益.另外,在码本比特数B∈[2,7]时,可以发现采用RVQ码本时系统容量无显著变化.而采用LBG码本时,当B从2增加到3时系统容量增加较显著,但是随着B的进一步增加系统容量逐渐达到某个渐进水平.总之,RVQ码本要优于LBG码本.

[J

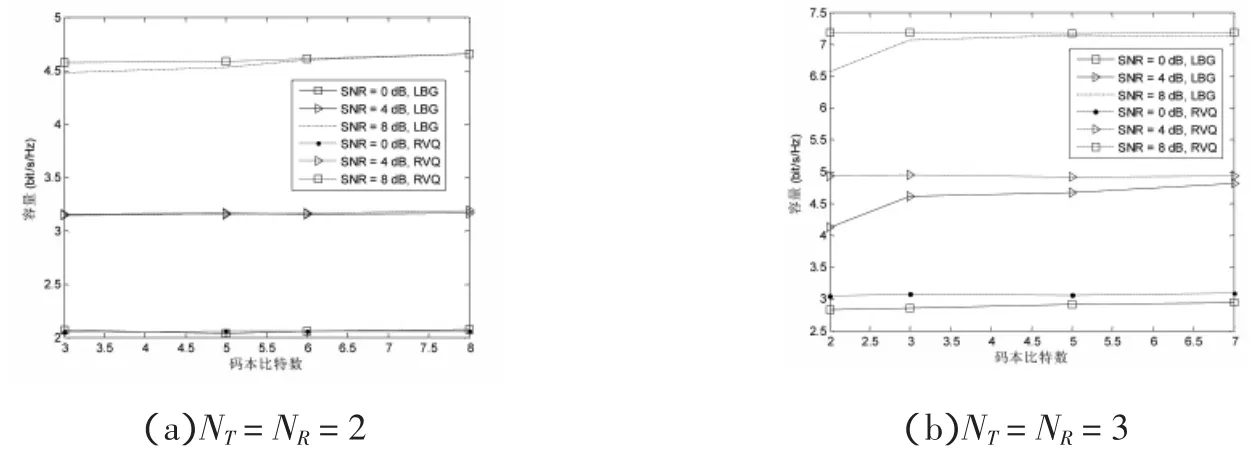
图3 LBG码本和RVQ码本性能对比

3.3 最小反馈比特数

为了保证系统的闭环容量不小于对应的开环容量,表1列出了在不同天线对下,采用RVQ方法和LBG方法分别所需的最小反馈比特数.表中的数据按公式(16)计算得到.可以看到,对于LBG方法,在固定的天线配置下最小反馈比特数随着信噪比的增加而增加;当发送天线小于接收天线数时,与收发天线数相同的情况相比,所需最小反馈比特数较大;采用RVQ方法比LBG方法所需的最小反馈比特要少,特别是对于(2,4)系统更为明显.

表1 采用RVQ方法和LBG方法分别所需的最小反馈比特数Bfeed

4 结 论

本文提供了不同系统参数配置下的闭环容量随着反馈比特数的变化曲线,并且给出了所需的最小反馈比特数与信噪比、天线对的关系.数值仿真结果表明:较低的反馈比特数将会产生相对开环系统的负容量增益,当反馈比特数大于等于某个门限值,系统将会产生正容量增益;对于LBG方法,所需最小反馈比特数随着系统信噪比的增加而增加,而RVQ方法所需的最小反馈比特数总体上差异不大;采用RVQ方法比LBG方法所需的最小反馈比特数总体上要小.

[1]Sesia S,Toufik L,Baker M.LTE-the UMTS long term evolution:from theory to practice[M].Wiley,2009:1-18.

[2]Ghosh A,Ratasuk R,Mondal R B,et al.LTE-advanced:next generation wireless broadband technology[J].IEEE Wireless Communications,2010,17(3):10-22.

[3]Telatar I E.Capacity of multi-antenna gaussian channels[J].European Transactions on Telecommunications,1999,10(6):287-304.

[4]Foschini G J,Gans M J.On the limits of wireless communications in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6:315-335.

[5]Li H,Ru G,Kim Y,et al.OFDMA capacity analysis in MIMO channels[J].IEEE Transactions on Information Theory,2010,56(5):4438-4446.

[6]Qin P Y,Guo Y J,Liang C H.Effect of antenna polarization diversity on MIMO system capacity[J].IEEE Antennas and Wireless Propagation Letters,2010,9:1092-1095.

[7]Lau V,Liu Y,Chen T A.On the design of MIMO block fading channels with feedback-link capacity constraint[J].IEEE Transactions on Communications,2004,52(1):62-70.

[8]Santipach W,Honig M L.Asymptotic performance of MIMO wireless channels with limited feedback,Proceedings of IEEE MILCOM,Boston,USA[C].New York:IEEE,2003:141-146.

[9]Yong C,Lau V,Yi L.A scalable limited feedback design for network MIMO using per-cell codebook,Proceedings of IEEE WCNC,Sydney,Australia[C].New York:IEEE,2010:1-6.

[10]Yellapantual R,Yao Y,Ansari R.Antenna selection and power control for limited feedback MIMO systems,Proceedings of IEEE VTC,Quebec,Canada[C].New York:IEEE,2006.

[11]Love D J,Heath R W.Limited feedback unitary precoding for spatial multiplexing systems[J].IEEE Transactions on Information Theory,2005,51(8):2967-2976.

[12]Heath R W,Lov D J.Multimode antenna selection for spatial multiplexing systems with linear receivers[J].IEEE Transactions on Signal Processing,2005,53:3042-3056.

[13]Linde Y,Buzo A,Gray R M.An algorithm for vector quantizer design[J].IEEE Transactions on Communications,1980,28:84-94.

[14]Lee J. Probabilistic limited feedback precoding in MIMO interference channels[J]. IEEE Communications Letters,2012,16(12):1964-1967.

[15]Zhang Y,Lei M.Robust Grassmannian prediction for limited feedback multiuser MIMO systems,Proceedings of IEEE WCNC,Daris,France[C].New York:IEEE,2012:863-867.

[16]Yu W,Rhee W,Boyd S,et al.Iterative water-filling for Gaussian vector multiple-access channels[J].IEEE Transactions on Information Theory,2004,50(1):145-152.

[17]Hassibi B,Hochwald B M.How much training is needed in multiple-antenna wireless links[J].IEEE Transactions on Information Theory,2003,49(4):951-963.

[18]Au-Yeung C,Love D J.On the performance of random vector quantization limited feedback beamforming in a MISO system[J].IEEE Transactions on Wireless Communications,2007,6(2):458-462.