基于Zadoff-Chu 矩阵的最优码本构造方法
李玉博,刘胜毅,张景景,贾冬艳
(1.燕山大学信息科学与工程学院,河北 秦皇岛 066004;2.河北省信息传输与信号处理重点实验室,河北 秦皇岛 066004;3.河北科技师范学院数学与信息科技学院,河北 秦皇岛 066004)
1 引言
码本是一类具有较低相关性的信号集,在同步码分多址(CDMA,code division multiple access)通信系统[1]、量子编码理论[2]以及压缩感知领域具有重要应用[3]。构造参数达到理论界限的最优码本是现代通信理论的重要研究课题之一,因此码本构造方法的研究受到人们的广泛关注。一般来说,码本C 由2 个参数进行表示,即(N,K),其中,N 表示码本的数量,K 表示码本的长度。码本的字符集是码本中所有码字的坐标所采用的不同复数值的集合,字符集大小是字符集中元素的数量。在实际应用中,字符集较小的码本具有重要的意义。另外,码本的最大互相关幅度值用 Ima(Cx)表示。在通信系统中,希望码本的最大互相关幅度值 Ima(Cx)越小越好,以尽可能消除信号之间的干扰。在压缩感知领域,具有低相关性的码本可用于构造测量矩阵。根据压缩感知理论可知,码本最大互相关幅度值Ima(Cx)越低,其对应的测量矩阵RIP(restricted isometry property)性能越好[2]。除此之外,在量子信息领域中[3],码本还用于构造SIC-POVM(symmetric informationally complete positive operator-valued measure)和无偏正交基(MUB,mutually unbiased base)。码本的参数受到理论界限的制约,当N ≥K时,称最大互相关幅度值满足Welch 界限的码本为最优码本;当N >K2时,称最大互相关幅度值满足Levenstein 界限的码本为最优码本。近年来,研究人员提出了很多近似达到Welch 界或Levenstein 界的码本构造方法。文献[4]首次利用差集构造了最优码本。Ding 等[5-6]进一步利用差集和几乎差集构造了参数达到Welch 界的最优码本。文献[7-10]利用分圆类方法构造了具有优良参数的码本。除此之外,还有一些利用bent 函数[11]、平坦函数[12]、有限域上的特征和理论[13-16]以及二元线性码[17]来构造码本的方法。
近年来,文献[18]提出一类基于二元序列与变换矩阵的码本构造框架。该框架包含了已有的许多码本构造方法,如文献[4-6]的方法等。该类方法有2 个关键因素:1)满足一定条件的变换矩阵的构造;2)二元序列支撑集的选取。现有的码本构造方法大部分都是基于已有的变换矩阵如离散傅里叶逆变换(IDFT,inverse discrete Fourier transform)矩阵、Hadamard 矩阵,通过选取不同的二元序列支撑集来构造码本。基于同样的思想,文献[19-20]通过选取一类新的二元序列构造了一类新的最优码本。本文放宽了文献[18]对初始变换矩阵的条件限制,构造了一类新的变换矩阵,并结合现有的一些特殊的整数集合构造了参数达到渐进最优的码本。
2 基本概念
一个参数为(N,K)的码本是一个复向量集合C={ C0,C1,…,CN-1},其中每个向量Cn=(cn,0,cn,1,…,cn,K-1)是长度为K 的单位复向量,其中0≤ n ≤N-1,。对于任意2 个向量Cn1,Cn2∈C,定义厄米特(Hermitian)内积为,其中(·)H表示向量的共轭转置。向量集合C 中最大互相关幅度值定义为
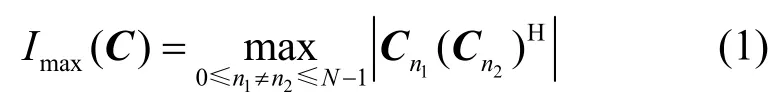
对于码本的最大互相关幅度值,有以下界限成立。
引理1[4]对于一个参数为(N,K)的码本C,其中N ≥ K,则有
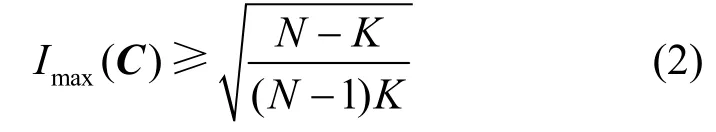
式(2)中等号成立的条件是当且仅当对于任意的0≤n1≠n2≤N-1,有
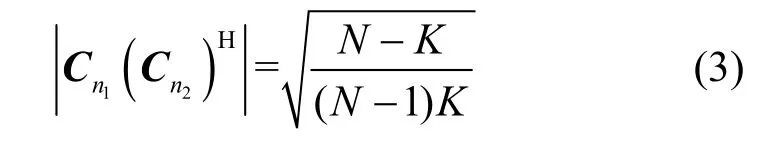
当式(3)成立时,则码本最大互相关幅度值达到Welch 界限,称为 MWBE(maximum-Welchbound-equality)码本;当N >K2时,不存在达到Welch 界的(N,K)码本,此时Levenstein 界更紧。
引理2[11]对于任意参数为(N,K)的实码本,若,则有
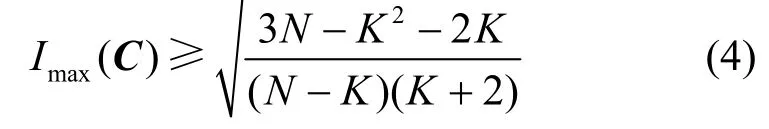
对于任意参数为(N,K)的复数码本,若N >K2,则有
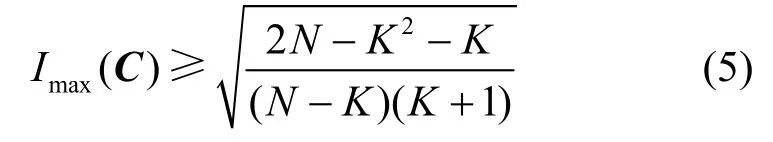
一般称达到Welch 界或Levenstein 界的码本为最优码本,对于最优码本的构造方法研究具有重要的应用价值。
设p 为素数,Fp表示包含有p 个元素的有限域,。令ZN={0,1,2,…,N-1}表示一个模N 的整数环。
定义1设q=pn是素数幂,p 为素数,令α 表示循环群的生成元,有限域上的乘法特征定义为
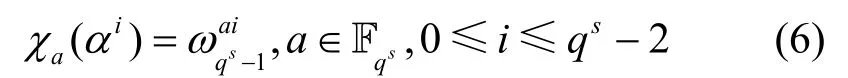
定义2设集合D={d0,d1,d2,…,dK-1}表示有限域Fp上一个子集,定义集合D 的差函数为,τ∈Fp。如果满足当τ 取遍 Fp上非0 元素时,差函数 fD(τ)取值为λ 出现p-1次,则称集合D 是有限域 Fp上的一个差集,参数表示为(p,K,λ)-DS。
显 然,对 于 差 集(p,K,λ)-DS,有K(K-1)=(p-1)λ成立。
定义3设集合D={d0,d1,d2,…,dK-1}表示有限域Fp上一个子集,定义集合D 的差函数为,τ ∈Fp。如果满足当τ 取遍 Fp上非0 元素时,差函数 fD(τ)取值为λ 出现t 次,取值为 λ +1出现p-1-t次,则称集合D 是有限域 Fp上的一个几乎差集,参数表示为(p,K,λ,t)-ADS。
定义4令D={d0,d1,d2,…,dK-1}表示整数环ZJ上一个含有K 个不同整数的集合,dk∈ZJ,0≤ k ≤K-1。集合D 的特征序列定义为一个二元序列a=(a0,a1,…,aJ-1),其中有

则称集合D 为序列a=(a0,a1,…,aJ-1)的支撑集。显然,序列的汉明重量。
定义5设N,γ 是2 个互质的正整数,则Zadoff-Chu 序列族的第γ 行序列可以表示为
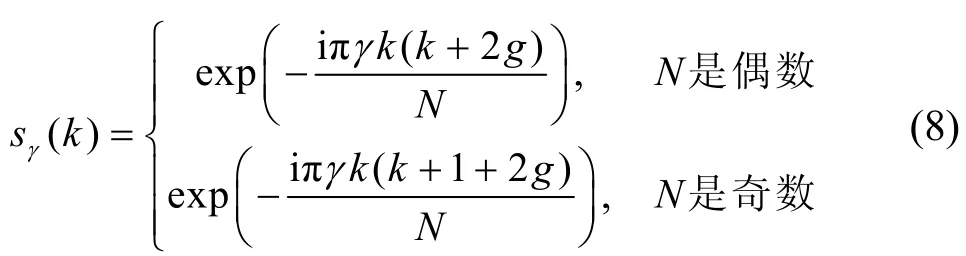
其中,k=0,1,…,N-1,g 是一个整数。
3 基于二元序列的码本构造框架
文献[18]提出一类基于二元序列的码本构造框架,其构造过程如下。
步骤1定义一个变换矩阵,令φi,l表示矩阵中任意元素,0≤i ≤J-1,0≤l ≤N-1。矩阵满足以下性质。
性质1每个矩阵元素具有单位幅值,即。
性质2任意2 个不同列向量满足=φi,l,0 ≤l1≠l2,l ≤N-1,0≤i ≤J-1。
性质3矩阵Φ 的第一列为全1 向量,即φi,0=1,0≤i ≤J-1。
性质4对于任意0<l≤N-1,有。
满足上述性质的变换矩阵已知的有N × N的Hadamard 矩阵和IDFT 矩阵。
步骤2取二元序列 a=(a0,a1,…,aJ-1),序列的汉明重量wt(a)=K,设集合D={d0,d1,d2,…,dK-1}是序列a 的支撑集。构造码本CΦ(a)={C0,C1,…,CN-1}为
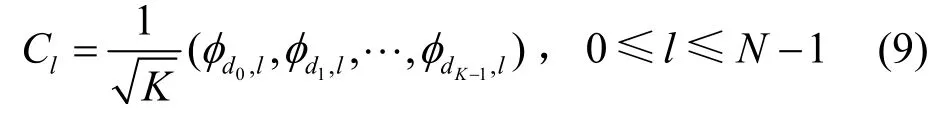
其中,Cl为构造的码本中的一个行向量,集合D 是变换矩阵Φ 的行索引集,即元素φdk,l(0≤ k ≤K-1)是矩阵中第 dk行、第l 列元素,则 CΦ(a)即为得到的(N,K)码本,其最大互相关幅度值 Imax(CΦ(a))可以由变换矩阵与二元序列的支撑集计算得到。
文献[18]构造的框架包含了已有的一些码本构造方法作为特殊情况。例如,当选取N × N阶的IDFT 矩阵作为变换矩阵Φ 时,若选取的二元序列对应的支撑集为差集时,得到的码本 CΦ(a)即为文献[4]的结果。若二元或复Hadamard 矩阵作为矩阵Φ,则选取的二元序列对应支撑集为几乎差集时,得到的码本 CΦ(a)为文献[5-6]的结果。该构造框架有2 个关键因素:1)变换矩阵Φ 的选取;2)二元序列a 的支撑集选取。基于该构造框架,文献[19]通过选取不同的二元序列构造了参数几乎最优的码本。同时文献[19]也指出,可以通过构造新的变换矩阵来构造新的码本,然而并没有给出新的变换矩阵构造方法。文献[20]同样采用Hadamard 矩阵作为变换矩阵,通过设计一类新的二元序列进而构造了一类最优码本。本文从另一个角度出发,通过设计新的变换矩阵来构造新的码本。
4 最优码本的构造
本文提出的新的构造方法介绍如下。
步骤1根据定义5,令g=0,γ =1,N 是偶数,得到Zadoff-Chu 矩阵的第一行。令,k=0,1,…,N-1,由此定义 Zadoff-Chu 矩阵为
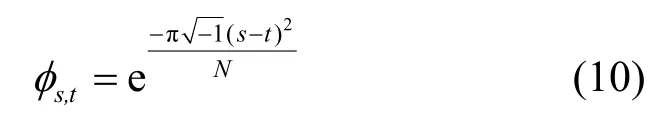
其中,0≤ s,t ≤N-1。文献[21]中令矩阵Φ 的N 为偶数来构造测量矩阵,而本文取N 为奇数的情况来构造码本。
步骤2设D={d0,d1,d2,…,dK-1}表示整数环ZN上一个含有K 个不同整数的集合,dk∈ZN,0≤ k ≤K-1。构造码本CΦ={C0,C1,…,CN-1}为
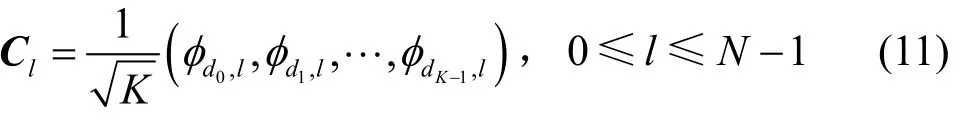
则 CΦ即为得到的(N,K)码本。
定理1令CΦ为本文新的构造法得到(N,K)码本,则最大相关幅度值为

证明设 Cl,Ct∈ CΦ,0≤t≠l ≤N-1,则有
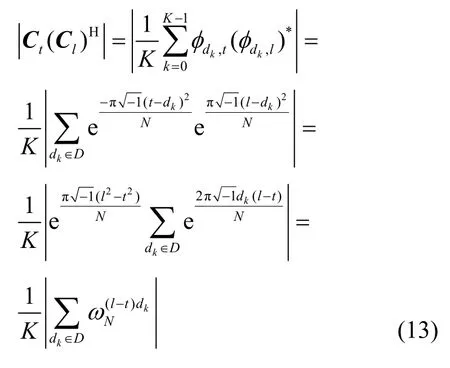
证毕。
4.1 基于差集的最优码本
引理3[5]令集合D={d0,d1,d2,…,dK-1}表示有限域 Fp上的一个差集(p,K,λ)-DS,则对于任意γ≠0(mod p)有
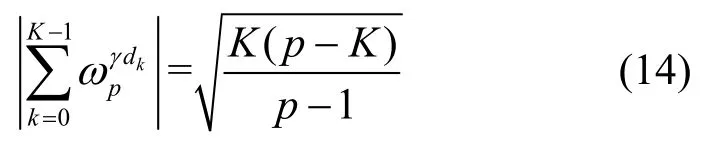
根据引理3,可以得到下面结论。
定理2令N=p为素数,若集合D={d0,d1,d2,…,dK-1}为有限域 Fp上的一个差集(p,K,λ)-DS,则式(9)定义的码本参数为(p,K),码本的字符集大小为2p,最大相关幅度值为,该码本达到Welch 界。
证明码本的最大相关幅度值可以由定理1 和引理3 直接得到。根据引理1 可知,该码本最大相关幅度值等于Welch 界,是一类最优的码本。
证毕。
例1令p=7,取集合 D={1,2,4},可知其是一个差集(7,3,1)-DS,得到(7,3)码本为
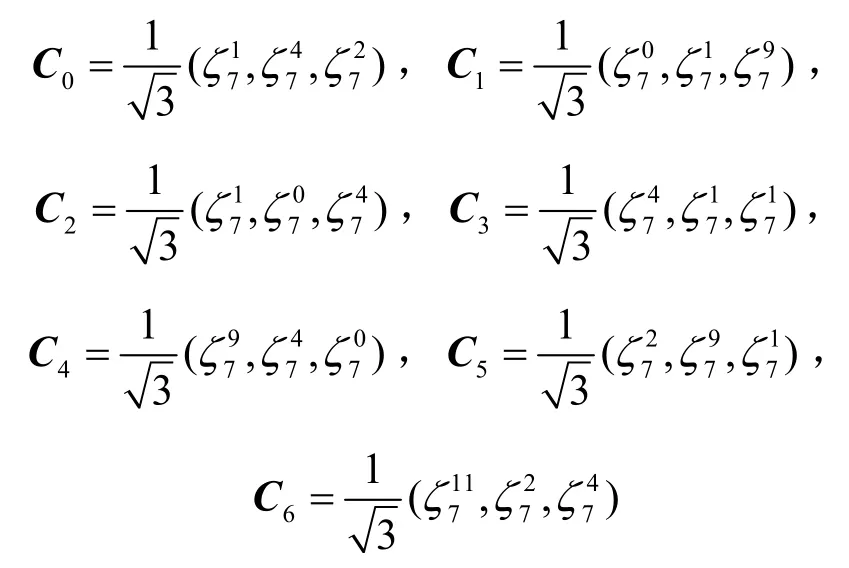
定理2 得到的码本与文献[4,18]具有相同的参数和相同的最大相关幅值,但不是同一类码本。由于变换矩阵的选择不同,2 类码本内部的元素也不相同。文献[4,18]的码本选取的变换矩阵是IDFT 矩阵,字符集更小;而定理2 构造的码本的变换矩阵是Zadoff-Chu 矩阵,限制条件更少,构造更灵活。例如,选取同样的差集 D={1,2,4},文献[4,18]得到的码本为
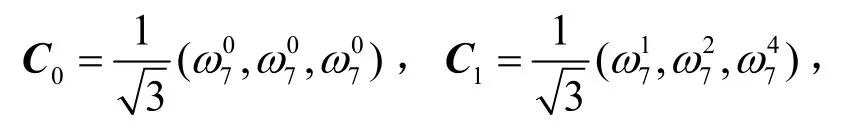
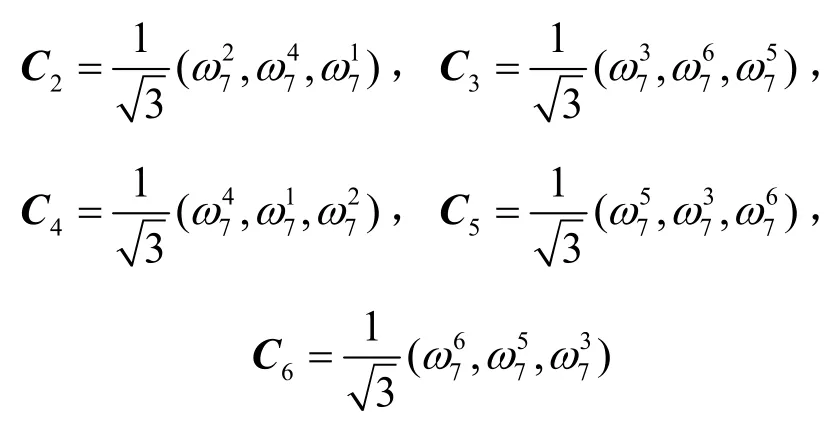
4.2 基于几乎差集的最优码本
引理4[5]令p=1(mod4),则2阶分圆类是有限域Fp上的几乎差集,参数为,-ADS。对于该几乎差集,Δ≠0,有
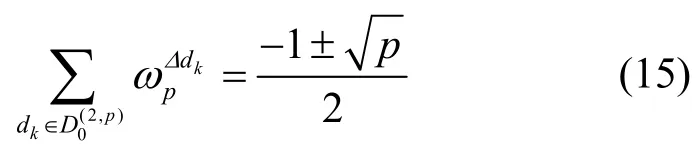
根据引理4,可以得到下面结论。
定理3令N=p为素数,若集合D={ d0,d1,d2,…,dK-1}为有限域Fp上的几乎差集,-ADS,即,则式(9)定义的码本参数为,码本的字符集大小为2p,最大相关幅度值为。该码本渐进达到Welch 界。
证明根据构造过程可知向量数目N=p,向量长度,计算其互相关幅度如下。由引理4可知,对于几乎差集,有≤。又由定理1 可得,码本最大相关幅度值为
可以看出,当p 增大时,该码本渐进达到Welch 界。
证毕。
4.3 基于特征和的最优码本
令 ξK表示K 维希尔伯特空间的标准正交基所构成的集合,即由下面K 个长度为K 的向量ei(1≤i ≤K)组成的集合为
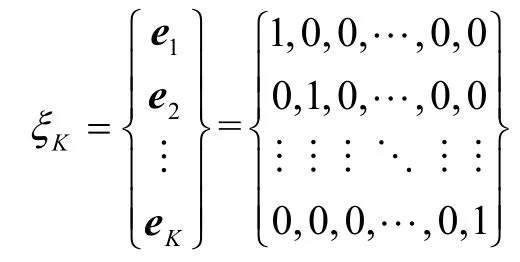
其中,e1=(1,0,···,0),e2=(0,1,···,0),·· ·,eK=(0,0,···,1)。
设q=pn是素数的幂,其中p 为素数。令a∈Fq,定义集合。有限域上的艾森斯坦和(Eisenstein sum)定义为
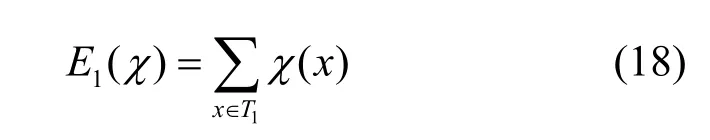
引理5[22]令χ 表示有限域上的非平凡乘法特征,对于任意,有
定理4令s=2,N=q2-1,a 是有限域的本原元,。选取集合D={d0,d1,d2,…,dK-1}为dk=logax,
设CΦ表示式(9)定义的码本,则CΦ∪ξK是(q2+q-1,q)码本,码本的字符集大小为2p+1,其最大互相关幅度为。
证明由上述构造过程可知向量长度K==qs-1=q,向量数目为N=q2+q-1。其互相关幅度值计算如下。
当 Cl,Ct∈ξK时,很容易得。
当 Cl∈ξK,Ct∈CΦ时,有。
当 Cl,Ct∈ CΦ时,根据定理1 有
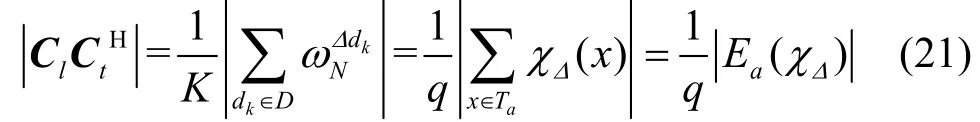
定理5码本CΦ∪ξK依照Levenstein界是渐进最优的。
证明对于参数为(q2+q-1,q)的复数码本CΦ∪ξK,其中N >K2,根据引理2 可得,最大互相关幅度值的Levenstein 界为式(5),即
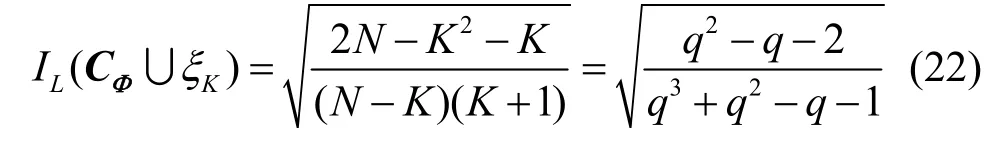
进一步可得
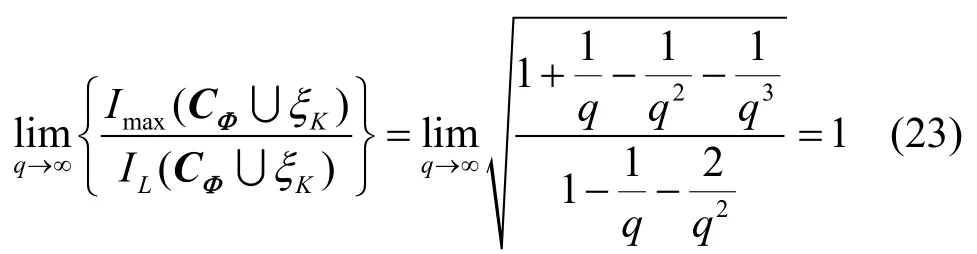
证毕。
5 最优码本构造方法的对比分析
对基于文献[18]的框架思想提出的几类最优码本构造方法进行比较,如表1 所示。
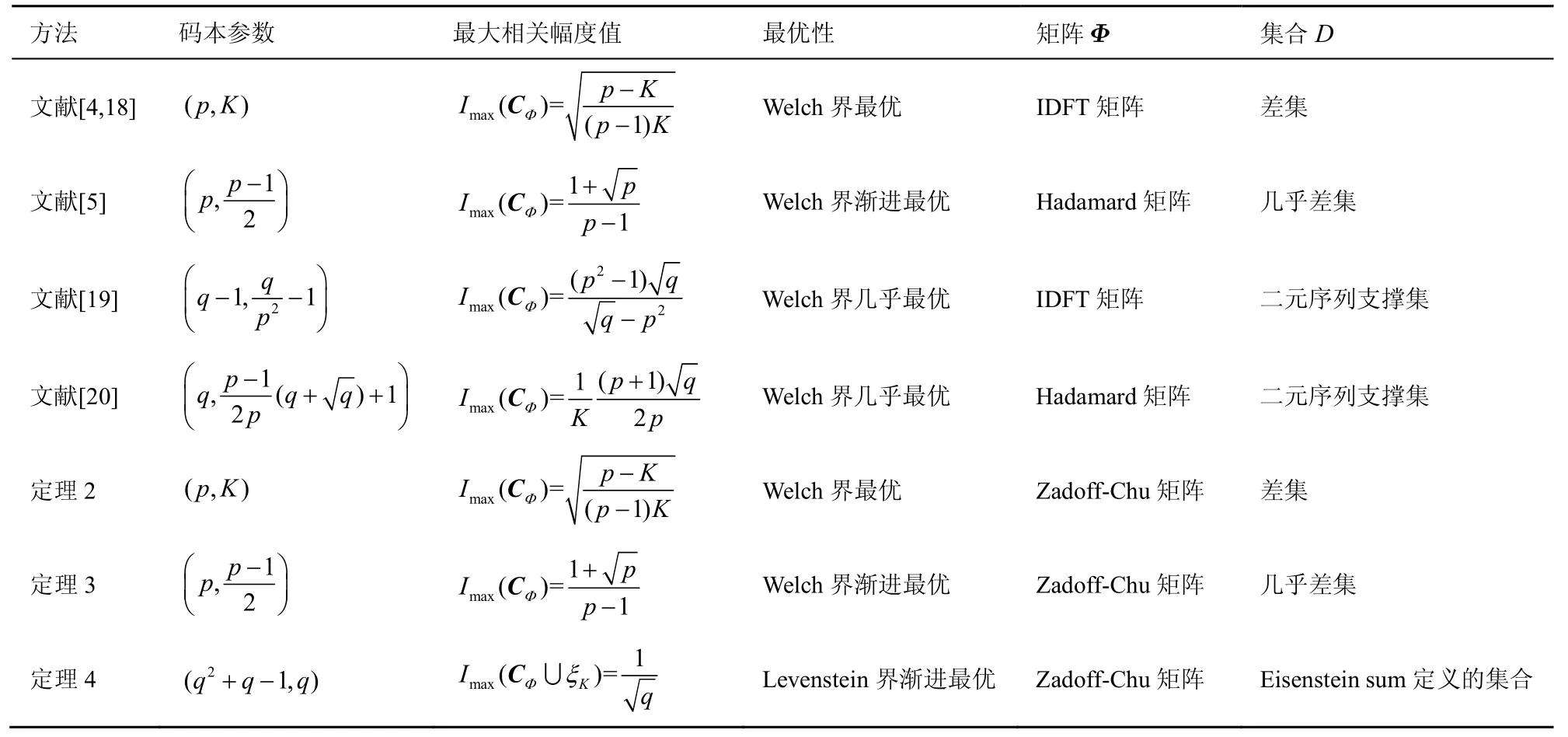
表1 几类最优码本的构造方法
由表1 可以看出,根据文献[18]提出的码本构造框架,可以通过选取不同的变换矩阵和集合来构造不同参数的码本。已有的方法都是基于IDFT 矩阵或Hadamard 矩阵,利用不同的集合来构造码本。本文提出了一类新的变换矩阵,利用已有的差集、几乎差集和有限域上的艾森斯坦和定义的一个集合构造了参数最优和渐进最优的码本。定理2 和定理3 与已有的文献[4,18]和文献[5]中的最优码本具有相同的参数和最大相关幅度值,因此可以为通信系统或信息处理提供更多的选择。定理4 构造出一类新的码本,依照Levenstein 界渐进最优,相比较依照Welch 界渐进最优的码本,最大互相关幅度值更小。虽然新变换矩阵放宽了限制条件使得字符集变大,但是在构造相同参数的码本时,变换矩阵在选取上具有了更强的灵活性。在构造压缩感知确定性测量矩阵等不要求字符集的应用中,本文构造的码本是更好的选择。
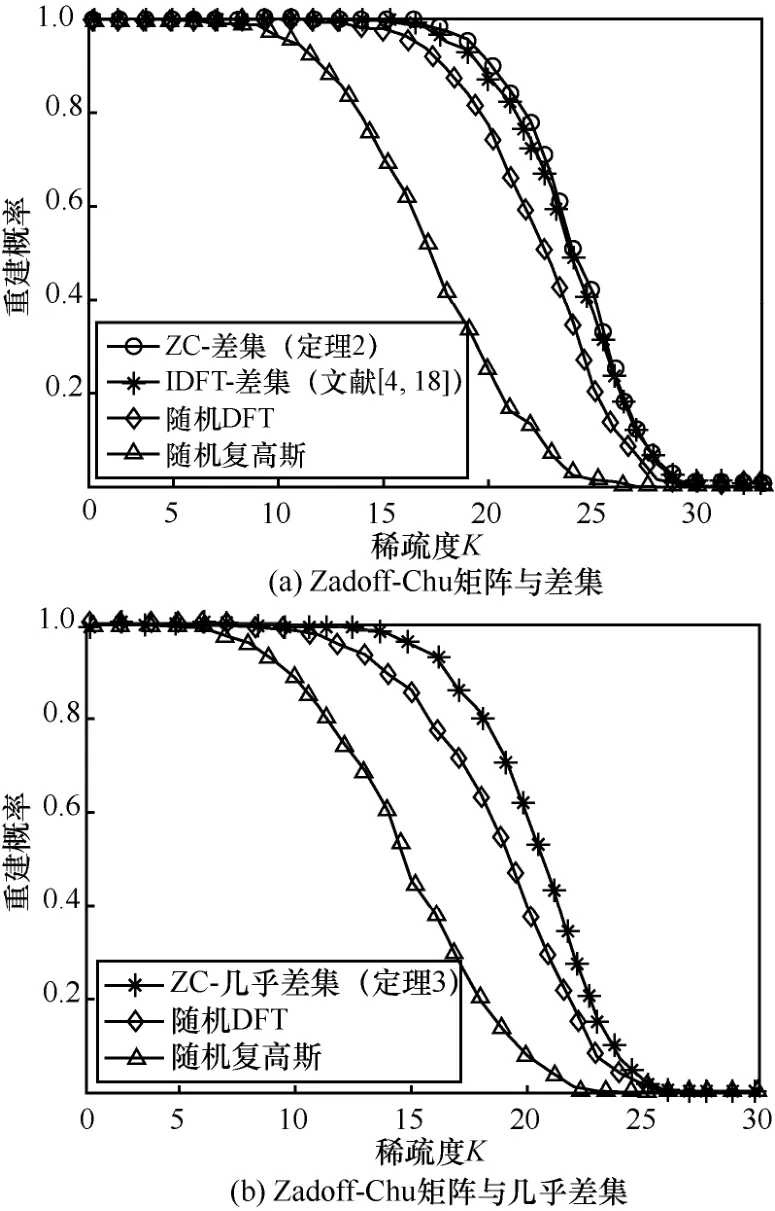
图1 稀疏度随重建概率变化曲线
由图1(a)可以看出,由本文定理2 中的码本构造的确定性测量矩阵在相同稀疏度时,重建信号的概率明显高于随机DFT 矩阵和随机复高斯矩阵。利用定理2 构造出的确定性测量矩阵与利用文献[4,18]构造的测量矩阵具有相同的参数,在重建信号的概率上甚至略高于文献[4,18]中的方法。同理,利用本文定理3 中的码本构造的确定性测量矩阵在重建信号的概率上明显高于随机测量矩阵。
6 结束语
基于文献[18]的码本构造思想,本文放松了变换矩阵的限制条件,提出了一类新的Zadoff-Chu 矩阵,并利用差集、几乎差集和有限域上的特征和构造了3 类码本,参数分别为(p,K)、和(q2+q-1,q)。本文构造的码本与已有码本的参数和最大互相关幅度值相同并且可以达到最优或渐进最优。本文方法可以为同步CDMA 通信系统提供大量可用码本,并且可以通过文献[3]的方法将本文得到的码本应用于压缩感知领域中确定性测量矩阵的构造,得到的确定性测量矩阵在重构信号的概率上明显优于随机测量矩阵。

