基于最小条件的平面拟合高精算法及编程
林 翔,江速勇,陈柏良,陈玉霞
(福建商业高等专科学校,福建 福州 350012)
1 基准平面
目前在几何量精密检测领域中,高精三坐标测量仪得到广泛的应用,如对圆度、平面度、直线度等各种形位误差的检测.在三坐标测量仪的支持下,不少种类的测量与误差评定技术水平,已经达到三维空间的高精度计算,只有少数如圆度误差评定的研究,一直停留在二维平面程度,只能处理二维坐标测量数据,与三坐标测量的实际脱节,不能真正满足实际工程中误差评定的需要,因此有必要对三维空间圆度测量数据的误差评定作深入的实质性研究.
三维空间圆度误差评定可以分为基准平面拟合与平面圆度计算两大环节,基准平面的拟合的精度,直接影响圆度评定结果的精度.国标《GB/T1182-2004》[1]规定,只有在以"最小区域法"求取平面度误差过程获得的拟合平面,才符合"最小条件"原则.
平面度属形状误差范畴,按国标[1]《GB/T 1182-2004》的表述,它是指被测物体表面相对于理想平面的变动量,此理想平面即所求的拟合基准平面.仅就平面度而言,通过"最小二乘法"求得的平面即可作为基准,以此基准即可计算出平面度误差,但它不符合"最小条件".
围绕这一判定准则,许多专家提出了不同算法,诸如"最小包容区域法"[3]、"有序判别法"[4]、"生物遗传算法"[5]等等,这些算法各有特色,也收到不错的计算结果,但由于这些近似算法的先天不足,虽能计算精度终归偏低.分析评定准则,其要点是求取两个平行的平面,把被测表面夹在其间,使两平面之距达到最小,因此可以在"最小二乘
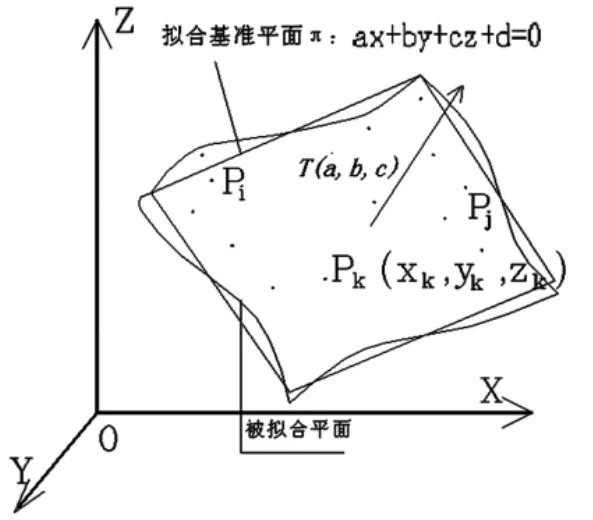
图1 基准平面与被测平面示意图
2 平面拟合
设平面上测量点集P={pk(xk,yk,zk),(k=1~n)},按照上述的解题大方向,可以选用"最小二乘平面"法,求取初始的基准拟合平面.设方程为π:ax+by+cz+d=0,如图1,点集P对于平面π的平面度误差值记若δ.此δ为统计意义下的平面度误差值,是国标《GB/T 1182-2004》[1]认可的,在评定精度要求不高的情况下已具有实用意义,如汽车零部件的检测.要达到高精度评定,还需研发更高精的算法.
经过对P与π之间距离最远点所表现出来的特性分析发现,提高平面度误差计算精度关键,是设法对π作细微转动,即有意识地改变平面法矢T(a,b,c),就有可能降低δ值.方法如下:
由"最小二乘"法得到的初始拟合平面为π,点集P={Pk,(k=1~n)}中到π距离之最大者、最小者分别为Pi、Pj,距离分别为δi、δj;记Ai为Pi在π的投影点,Aj为Pj的投影点,δ=δi+δj,此即初始平面度误差值.
再设ε是一个甚小值,沿AiPi方向距Ai点ε处取Ai'点,沿AjPj方向距Aj点ε处取Aj'点;记Q为Ai'Aj'中点(Q在π上),在π上再取一点Q',使Q'Q⊥Ai'Aj'.以Ai'、Aj'、Q'三点构造一个新的平面π',显见π与π'之夹角很小,可将π'看作π绕Q'Q作细微转动而获得;从方程来看,就是π的法矢T(a,b,c)发生细微改变.
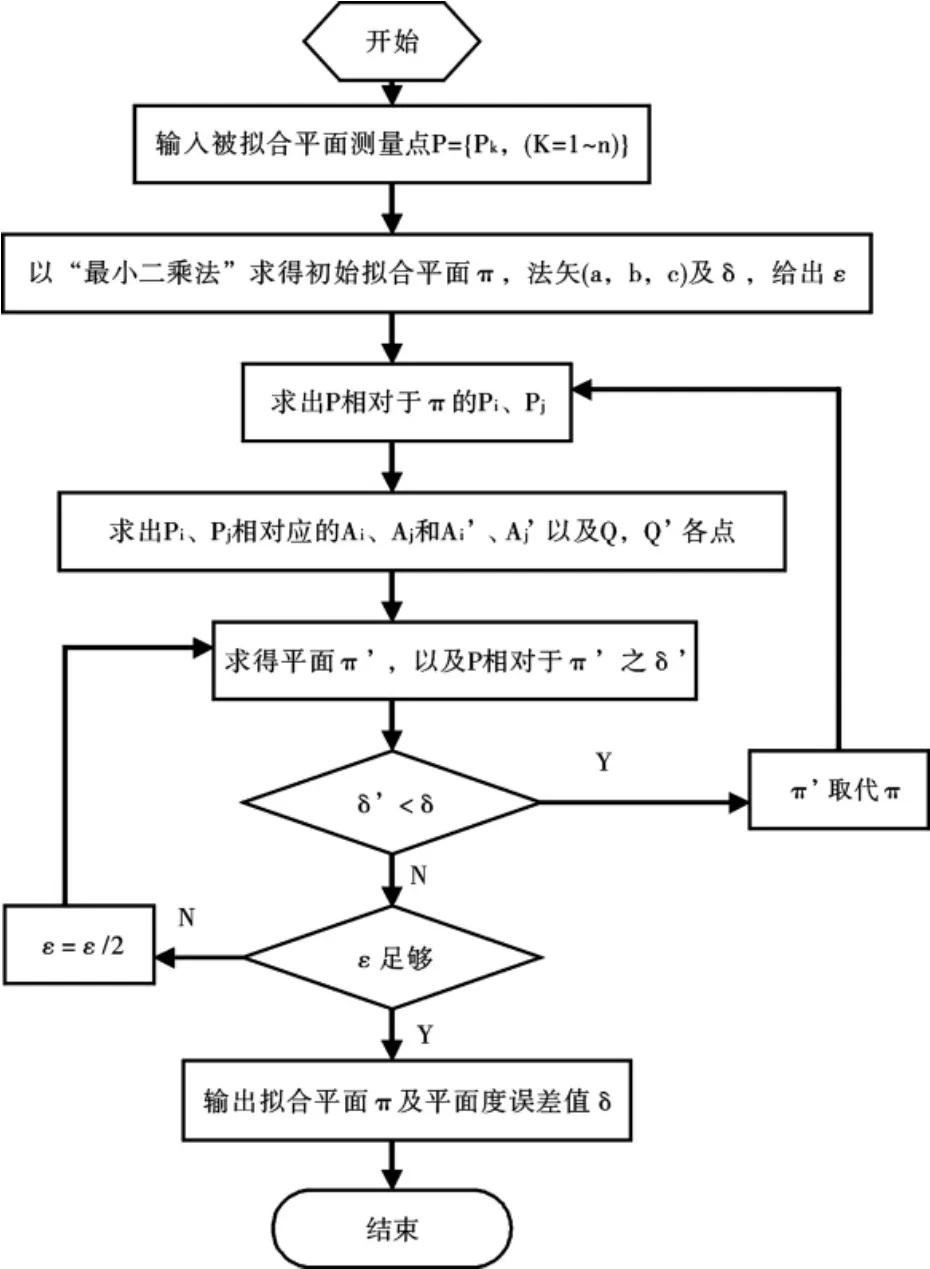
以 Pi、Ai'、Pj、Aj'4点构造平面 π1,再以π1对平面π垂直剖切,剖面如图2所示,PiAi=δi,PiAi'=δi',易见,在ΔPiAi'Ai中,PiAi' δ能否降下来,须通过点集P对新平面π'求平面度误差值δ'与δ作比较并加以判断: 1、如果降下来了,π'取代π,再重复上述操作对π作细微转动; 2、如果没有降,则将ε值减半,重新构造π',计算δ'并与δ比较,观其下降与否; 3、如果ε经多次减半缩小成为非常小的值,转动后得到的π'再也不能令δ'下降,且δ'与δ之差极小,达到了计算精度要求,则停止计算,π即所求的符合"最小条件"的拟合平面. 图2 Pi、Pj等各点与平面π、π'关系图 图2中,P距π的两个最远点为Pi、Pj,Pi在平面π的投影点为Ai,在平面π'的投影点为Ai',在△PiAiAi'中∠PiAi'Ai是钝角,由于钝角的任一邻边长度必然小于对角边,即PiAi' δ'=δi'+δj'=PiAi'+PjAj' 算法设定的终止条件为:当ε经多次缩半而变得甚小,π即使进行甚小的转动,δ也不能下降,且δ与δ'之间相差达到计算精度要求,则停止计算.因为此时δ已非常接近谷底,非常接近平面度误差真值了,且符合国标《BB/T 1182-2004》[1]中"最小区域法"平面度误差的判定条件,所拟合的π即为符合"最小条件"的基准平面. 以"最小二乘法"平面为初始基准平面,既保证算法在收敛区间内进行,又有利于算法的快速收敛. (1)"最小二乘法"求平面过程简述: 平面点集P={Pk,(k=1~n)},初始拟合平面π:ax+by+cz+d=0,为讨论方便,令T(a,b,c)为单位矢量,则任一点Pk到π的距离为: "最小二乘"拟合平面的目标方程为: 要使 D 达到最小,只要令:∂D/∂a=0,∂D/∂b=0,∂D/∂c=0,∂D/∂d=0,及 a2+b2+c2=1即可; 联解以上5等式,就能求得初始平面π的法矢T(a,b,c)和d各值,平面π的方程也就确定;求出δi、δj值,δ=δi+δj即为P在"最小二乘法"意义下的平面度误差值. (2)在初始拟合平面π的基础上实施本算法: 由上已经获取Pi、Pj二点,以及对应的δi、δj二值,设Pi、Pj在平面π的的投影点分别为Ai、Aj;连线Ai、Pi及Aj、Pj,沿AiPi方向距Ai点ε处取点Ai',沿AjPj方向距Aj点ε处取点Aj';求出Ai'、Aj'的中点Q,在π上求得点Q',使直线Q'Q⊥Ai'Aj'; 以Ai'、Aj'、Q'三点构造平面π',求出P到π'的距离之两个极值,记作δl'、δm',δ'=δl'+δm',比较δ'、δ并作如下判断: 1)如果δ'<δ,平面π'便取代平面π,重新如法炮制求取新的平面π',并进行同样的计算、判断; 2)如果δ'≥δ,分两种情况处理: a、将ε值减半,重构平面π',算出δ',返回到步骤1)重新作判断; b、如果ε已经缩小为非常小的值,δ与δ'相差达到精度要求,满足计算的终止条件,停止计算,π即为满足"最小条件"拟合基准平面. (3)特殊情况的处理 在上述计算过程中,如果Pk(k=1~n)到平面π的正最远点、负最远点不是唯一的,即"Pi"、"Pj"点不止一个,作如下处理:设有U个"Pi"、V个"Pj"(U、V≥1),将U个"Pi"与V个"Pj"进行两两配对,产生U*V个组合,每一个"Pi"、"Pj"组合,都可以通过上述(2)计算过程求得相应的拟合平面π'和δ'值.取U*V个δ'中最小者,记作δ'min,如果δ'min小于δ,则该δ'min及所对应的平面π',取代δ与π,然后周而复始继续计算、判断,直至满足终止条件. (4)程序流程框图见图3. 图3 程序流程图 (5)编程 选择既长于计算又具有绘图功能的C语言作为编程语言.程序(略). 上述从理论上证明了算法收敛于"最小区域",还须在实际中应用以检验程序的功能.课题组对程序进行了数十个算例进行验算,算例均取自已发表的其他专家论文、专著或各种标准,将计算结果与原文比较表明本算法计算得到的平面度误差值之精度都达到或超过原作,是知所拟合之平面亦优于原文.以下取出其中10个算例予以说明,计算结果中略去d值,因其实际上与平面度计算评定无关. 文献[2]提供的一个算例,被测平面上有25个测量点.原文给出的平面度误差最佳者为6.55 μm;用本程序计算得出的平面度为6.550 0 μm,拟合基准法矢为T(-0.000002,0.000005,1.00); 文献[6]之p90给出了一个算例,被测平面上3*3=9个点.原文给出的平面度误差为0.004 1;用本程序计算,得到的平面度误差为0.003 9,拟合平面法矢为T(1.997 292,0.997 622,1.000 0); 国标《GBT/1337-1989》[7]给出了两个算例,分别是被测平面上3*3=9、5*5=25个点.原文计算得出的平面度误差分别为100、7.7;用本程序进行计算,得出的平面度误差分别为: 100.000 664,拟合基准法矢T(-0.000 050,0.000 100,1.00); 7.136,拟合基准法矢T(-0.000 002,-0.000 002,1.000); 文献[8]给出了一个算例,被测平面上10*7=70个点.原文提供的平面度误差为7.81μm;本程序计算得出的平面度误差为 7.737 5 μm,拟合平面法矢 T(0.205 000,0.488 125,1.00); 专著[9]及文献[10]都给出了同一个算例,被测平面上5*5=25个测量点,原文给出的平面度误差为25 μm;本程序计算得出的平面度误差为10.1μm,拟合基准平面法矢T(0.000 118,-0.000 014,1.00); 同样对文献[3][4][5][11]所提供的算例进行验算,原文给出的平面度误差值分别为30.25 μm、6.55 μm、8.755 6 μm、8.5 μm;本程序计算的结果为 30.246 6 μm、6.550 0 μm、6.550 0 μm、8.500 0 μm. 比较彼此的计算结果,显然本程序计算得出的平面度误差值精度均优于原文,更符合"最小条件"原则,因此所拟合的基准平面也优于原文. 以"最小二乘法"求取的平面为初始拟合基准,继续以"最小区域"为目标寻找新算法,逐步令误差计算向"最小区域"逼近,不仅在理论上证明了算法的收敛性,并经过编程及许多实例加以验证,从运行过程与验证结果来看,本程序实现了项目开发的第一个目的,运算稳定、结论可靠.本程序在"奔4"微机上运行,一般性算例运行不到一秒钟,说明收敛速度很快,具备实用意义,为进一步开发高精度三维空间圆度评定程序,打下了决定性的基础. 本程序的另外一个特点是不要求检测点按网格均匀分布.为计算上的方便,测量时宜将被测平面置于与三维坐标系的xoy平面上,尽量与z轴垂直(不强求完全垂直). [1]GB/T 1958-2004,产品几何量技术规范(GPS)形状和位置公差检测规定[S]. [2]JJG 117-2005,平板检定规程[S]. [3]吕震宇.一种使用最小包容区域法基于旋转变换求解平面度误差的方法[J].河北理工学院学报,2000,2(1);47-56. [4]张之江,于瀛洁,张善钟.平面度误差最小区域新算法-有序判别法[J].计量学报,1998,19(1):15-21. [5]温秀兰,宋爱国.基于实数编码的改进遗传算法及在平面度误差评定中的应用[J].计量学报,2003,24(2):88-91. [6]陈基伟.工业测量数据拟合研究[D].同济大学工学博士学位论文,2005,11. [7]GB/T 11337-1989,直线度、平面度误差检测[S]. [8]崔长彩,车仁生,罗小川,等.基于实数编码遗传算法的平面度评定[J].光学精密工程,2002,10(1):36-40. [9]罗南星.几何量测量技术简明教程[M].机械工业出版社,1993,5. [10]倪爱晶,郑联语.基于形状误差不确定度的大尺寸测量系统优化配置方法[J].计量学报,2011,,32(4):289-295. [11]彭祖行.形状误差的优化算法[J].计量学报,1992,13(4):245-250.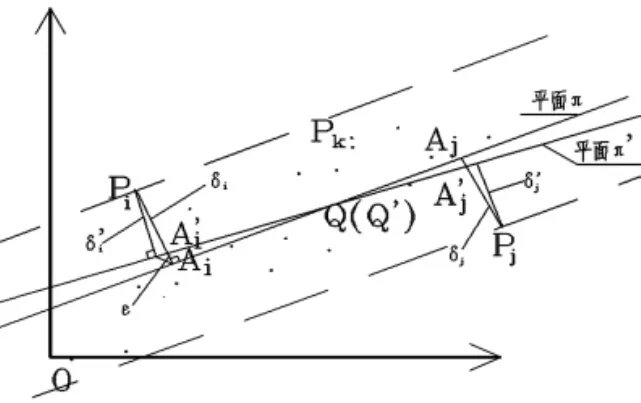
3 算法收敛于"最小区域"
4 算法的实现
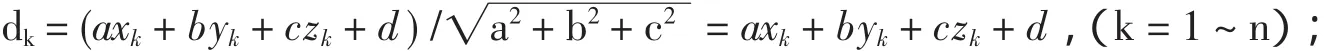
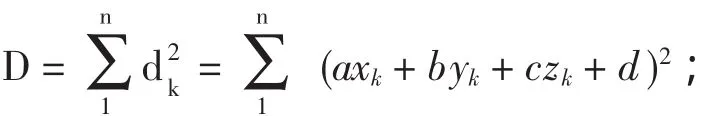
5 程序验证
6 结语

