基于局部彼得罗夫-伽辽金法的超长桩受力分析

吴 鸣,钟永国

(汕头大学土木工程系,广东 汕头 515063)

0 引言

我国沿海地区地质条件极其复杂,如广东、上海等沿海深厚软土达150~400 m,80 m以上超长桩已成为软土地区超高层建筑和某些安全等级要求较高的建筑物桩基常用的一种桩型.桥梁工程50~100 m长桩已十分常见,如我国杭州钱塘江六桥(在建)采用的钻孔灌注桩桩长达130余米,而国际上最深已达150 m.

随着桩长与桩径的增加,其承载性能及其影响因素更加复杂,现行规范中仍沿用普通桩的设计理论,即通过预估桩侧摩阻力和桩端阻力后相加并除以某一安全系数的方法得到,这一设计方法显示其局限性.大量的试验分析表明,基桩的侧阻和端阻发挥不同步,如果按照统一参数计算缺乏确切的安全度概念,这一问题在超长桩的设计中尤为突出;而超长桩桩侧阻在桩身中部常存在强化效应,又使其设计存在一定的承载潜力,这种一方面基桩已具有一定承载潜力,另一方面设计人员仍试图以增大桩长提高基桩竖向承载力的矛盾,均源自于工程设计人员缺乏对超长桩承载性状的深入了解,因而根据现行规范对超长桩的设计是不完善的,也是不合理的.实际工程中经常出现因桩基沉降过大等引起的工程事故,或桩基设计中越来越保守的趋势和严重浪费的现象,因而开展超长桩的承载性能与设计理论研究具有重要的工程意义和较大的经济价值,也是工程界的迫切要求.

在竖向荷载下,超长桩桩土之间往往出现滑移,甚至脱开,桩周土往往处于塑性变形状态,传统的数值计算难以满足如此要求,有限元-有限层法虽然能近似考虑土的非线性,计算简单,但是对于土的开裂,滑移等也显得力不从心,在众多数值方法中,有限单元法发展得较为成熟,其可同时考虑众多影响因素,如土的非线性、固结时间效应以及动力效应等,但在用轴对称有限元法对轴、横向荷载下超长桩进行承载性能分析时,仍存在以下问题:①大变形及开裂问题处理;②桩土接触面处理.至于其它数值方法,如流形元法、界面元法也难以很好地克服桩土接触面问题.可见,超长桩承载性能研究的突破很大程度上依赖于深入掌握桩土体系的相互作用机理,并引入合适的数值计算方法进行分析.本文引入最近发展的全新的数值计算方法-无网格法,用来分析大变形条件下层状地基中竖向荷载下超长桩的承载性能及其影响因素,以此修正和完善超长桩的承载机理.既可克服有限元方法的局限性和主要缺点,为无网格法在桩基工程领域的应用做一个有益的尝试,也为桩基的荷载传递机理及桩土共同作用分析提供了一条新的思路和方法.

1 无网格局部彼得罗夫-伽辽金法(MLPG)基本原理

无网格法与有限元法利用插值建立近似函数不同,它是在计算点邻域内通过逼近得到局部最优近似,然后由这些局部最优近似再获得求解域内的全局近似函数.在采用无网格法对承受竖向荷载作用的基桩进行分析时,考虑桩土共同作用情况的位移协调,基于计算点在桩土计算域内进行近似.

1.1 移动最小二乘近似(MLS)[1-4]

以二维问题为例来说明移动最小二乘函数的构造.考虑位于全域Ω内一点x的邻域(子域)Ω,为了得到近似函数u在子域Ωx内的分布,则在有限个随机分布的节点xi(i=1,2,…,n)上,函数u的近似值uh(x)(∀x∈Ωx)可定义为

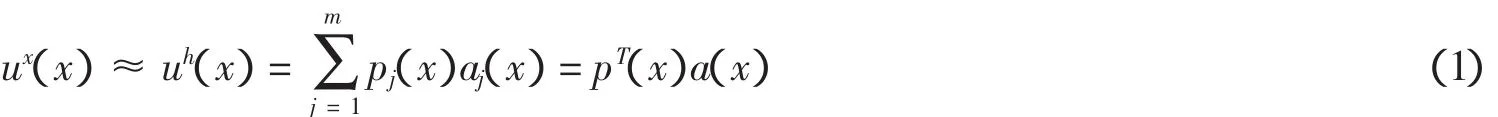
式中a(x)为一系数向量,可表示为

注意,式(2)中的系数向量a(x)是x的函数.该系数a可以通过对下列加权离散L2范数取极少而得到

式中n为包含在权函数w(x-xi)≠0的x支持域中的节点数,ui为u在x=xi处的节点参数,式(3)为一加权残量的泛函,它利用未知场变量节点参数值和其近似而构成.由于MLS近似式中的节点数n通常大于未知系数m,故近似函数uh将不通过节点值.

J关于a(x)求驻点值可得到:

上式运算后可得:

式中Us为支持域中所有节点的节点场函数参数所形成的向量.

由式(5)求解a(x)可得到

代入式(1)可得到

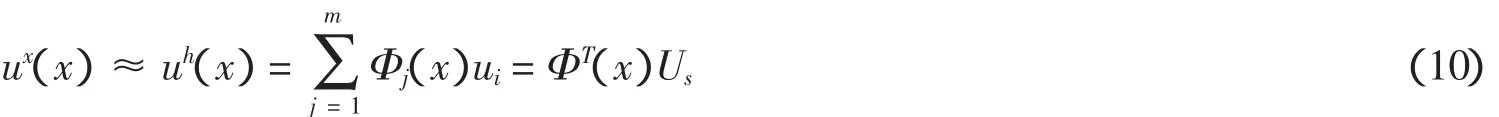
其中

1.2 无网格局部彼得罗夫-伽辽金法(MLPG)

弹性力学中MLPG的局部弱式可通过以下加权残量法得到:

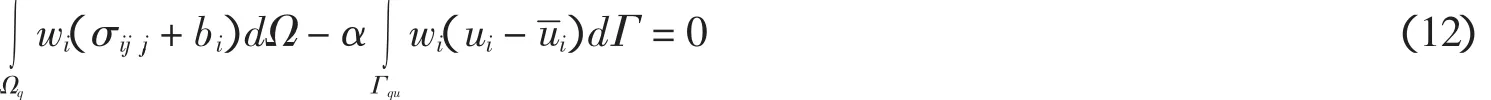
式中w为权函数,第二项积分用于施加位移边界条件.这是因为MLPG中的MLS形函数不具备Kroneker δ函数性质,从而采用罚函数法施加位移边界条件.Ωq是结点i的局部积分域,Γqu是与积分域Ωq相交的那部分位移边界,α是惩罚因子.本文中统一采用相同的惩罚因子.

采样点X处的位移可采用MLS形函数近似表示为:

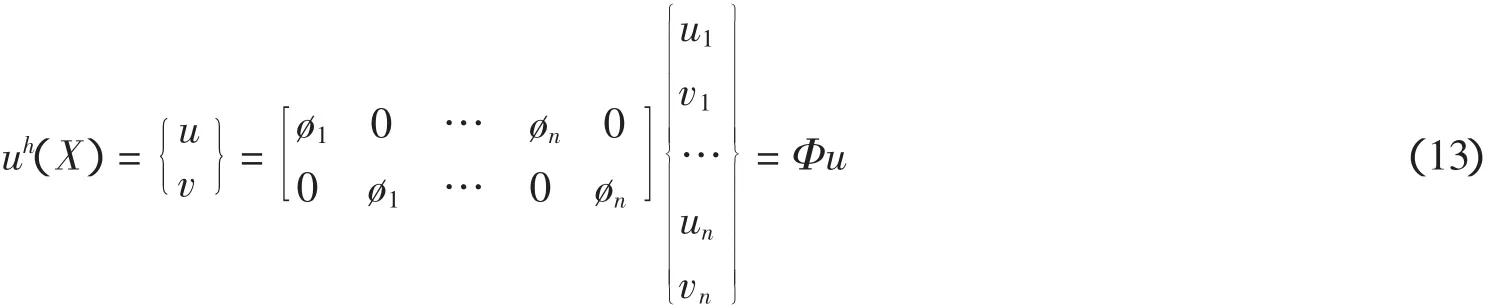
式中Фi为MLS形函数,Ф为有MLS形函数所组成的矩阵.

对(1)式左边第一项第一部分进行分部积分

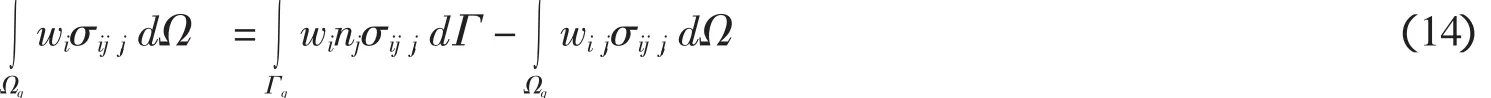
式中nj为边界上单位外法线向量的第j个分量.把(2)、(3)式代入(1)式进行离散、合并整理后可以得到

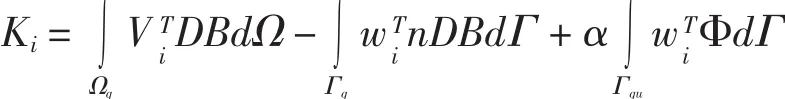
然后对问题域内所有N个场节点应用(15)式,组装即可得到总体系统方程.MLPG的系统方程为离散线性代数方程形式,即

解此方程可得到结点位移参数,进而利用(2)式可求得问题域内任意点的真实位移,从而可求得应力和应变.

对于位移边界条件,采用罚函数法进行处理.对于桩、土这两种不同的材料界面,采用Cordes等[6]给出的处理材料不连续问题的方法.

2 竖向荷载作用下基桩大变形处理方法

采用完全的拉格朗日法迭代计算.每级荷载增量为△Pi,在第i个增量步迭代收敛后,可由第i个增量步开始时的切向刚度矩阵[K]i-1(其中包含了第i个增量步以前所有加载过程中各种非线性因素对桩土系统刚度矩阵的贡献)提取线性荷载值,相应的提取非线性荷载值的方程可表示为

式中 [K]i-1为第i个增量步开始时系统的切向刚度矩阵;[△K]σ为系统几何刚度矩阵,它表示大变形情况下初应力对结构刚度的影响,即从第i个增量步开始算起的与系统荷载增量△Pi有关的函数;{Δd}为增量位移;{Δf}为增量外荷载、体力和面力矩阵.针对MLPG法(18)式最终简化为

式中,[K]为对桩土分析域各节点按权重和形函数在其定义域积分得到的刚度矩阵.

3 算例分析

本文以Microsoft Fortran Powerstation语言编制了基于局部彼得罗夫-伽辽金法的超长桩受力分析程序.程序编制以层状横向各向同性弹性半空间地基模型为基础.以文献[7]锡宜高速公路锡澄大桥试桩为分析对象:桩径d=100 cm,桩长l=43.0 m,长径比l/d=43,桩侧土层以亚粘土为主,桩端土层为粘土层;以及文献[7]郑州试桩为分析对象:桩径d=100 cm,桩长l=60 m,长径比l/d=60,桩侧土层以亚粘土、亚砂土为主,桩端土层为亚砂土层.计算参数如下表:

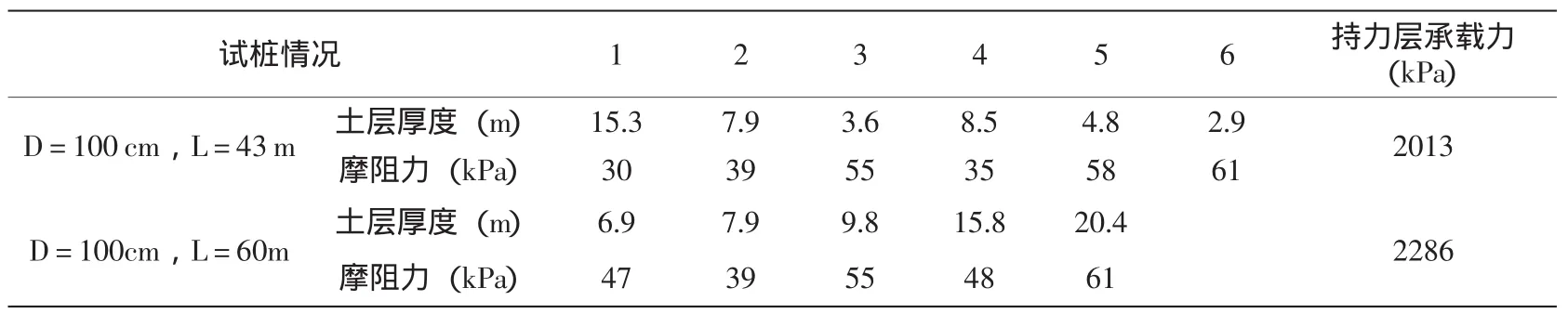
表1 试桩场址参数

使用本文方法进行沉降、承载力分析的结果与试桩结果对比如表2,表3所示.

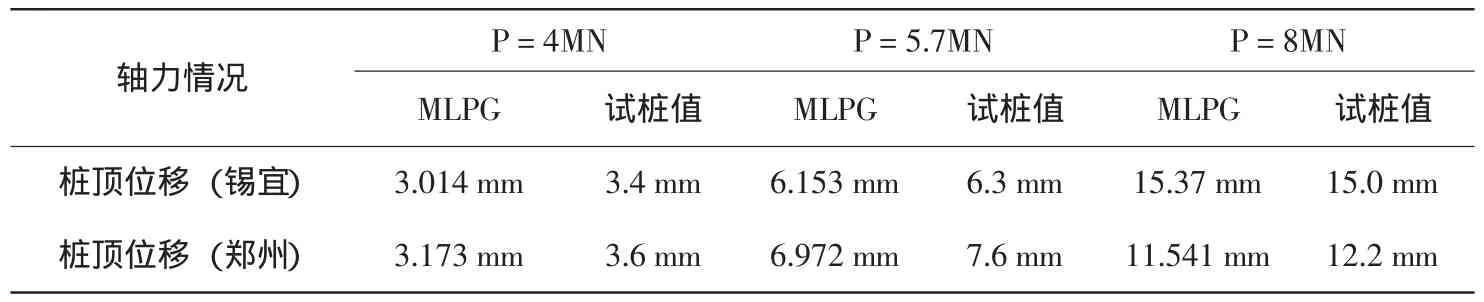
表2 桩顶沉降计算对比

由表2可得知:锡宜试桩沉降计算值与实测值误差最大为11.35%,最小为2.33%;郑州试桩沉降计算值与实测值误差最大为11.86%,最小为5.4%,吻合较好.

表3 竖向承载力计算对比(kN)

摩阻力的变化情况:

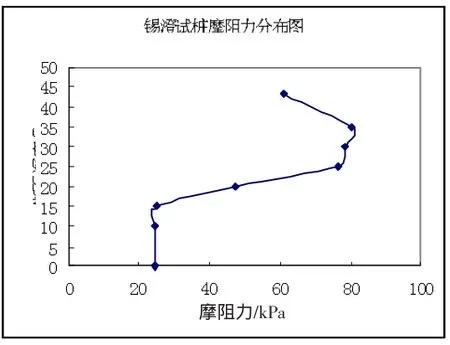
图1 锡澄试桩摩阻力分布图

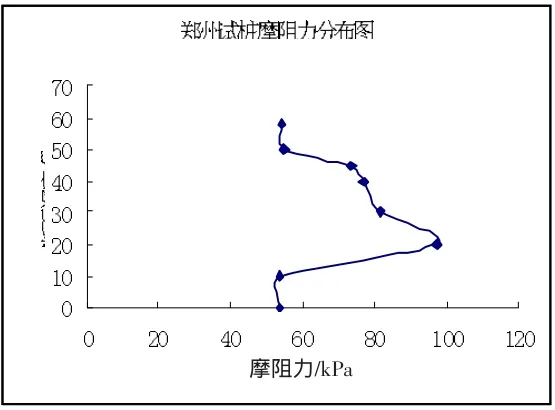
图2 郑州试桩摩阻力分布图

计算结果表明,按规范方法计算得到的单桩极限承载力小于实测值.而按本文方法计算的单桩极限承载力和实测的结果较吻合.计算过程中还发现,在距离桩顶约0.4-0.6 L处,侧摩阻力均具有明显的硬化效应,与试桩情况符合.

4 结 论

(1)按规范方法计算得到的单桩极限承载力一般都小于实测值,而按本文基于局部彼得罗夫-伽辽金法(MLPG)、考虑超长桩大变形运算程序的计算结果,与试桩结果更为接近.

(2)随着荷载的增加,超长桩的有效桩长逐渐增大;在距离桩顶约0.4-0.6 L处,侧摩阻力具有明显的硬化效应.

(3)有待进行更深入的理论研究以及更多的案例比对,以完善新方法.

[1]Liu G R,Gu Y T.An introduction to meshfree meshods and their programming[M].New York:Springer Publishing Company,2005,7.

[2]赵明华,汪优,王靓.水平受荷桩的非线性无网格分析[J].岩土工程学报,2007,29(6):907-912.

[3]赵明华,刘敦平,邹新军.横向荷载下桩-土相互作用的无网格分析[J].岩土力学,2008,9(29):2476-2480.

[4]贺炜,陈永贵,梁斌.超长桩承载性状分析的无网格局部彼得罗夫-伽辽金法[J].南华大学学报,2009,23(2):101-106.

[5]赵明华、吴鸣.桥梁桩基计算与检测[M].北京:人民交通出版社,2000,1.

[6]Cordes L W,Moran B.Treatment of material discontinuity in the element-free Galerkin method[J].Computer Methods in Applied Mechanics and Engineering,1996,139(1-4):75-89.

[7]钟闻华,石名磊,刘松玉.超长桩荷载传递性状研究[J].岩土力学,2005,26(2):307-318.

[8]JTG D63-2007,公路桥涵地基与基础设计规范[S].