两总体方差差异的U统计量检验法

王 敏

(鲁东大学数学与信息学院,山东 烟台 264025)

0 引 言

对两总体方差差异的检验在实际应用中是较常见的,但目前常用的F检验法是在假定总体为正态分布的情况下进行的,在非正态场合对该问题的研究很少.

本文在任意总体情形下,给出了两总体方差差异的U统计量检验法,并讨论了检验统计量的相合性,渐近正态性及检验的功效.

设X1,X2…Xm为来自总体X的简单随机样本,样本均值为,样本方差SX2,X的分布函数为为来自总体Y的简单随机样本,样本均值为,样本方差SY2,Y的分布函数为F(2y),EY=μ2,VarY=σ22<∞,假设两样本相互独立,欲检验H0:σ21=σ22,H1:σ21>σ22.

1 U统计量的建立

对于样本X1,X2…Xm及任意的1≤α1,α2≤m,令h(1α1,α2)=(Xα1-Xα2)2,对

于样本Y1,Y2,…Yn及任意的1≤β1,β2≤n,令h(2β1,β2)=(Yβ1-Yβ2)2,同时令

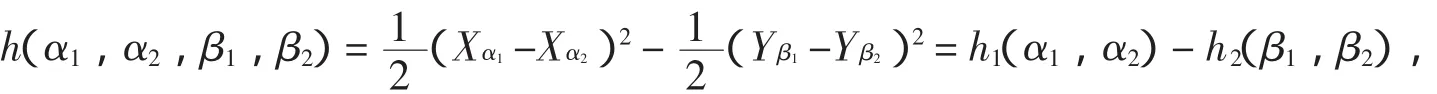
又令

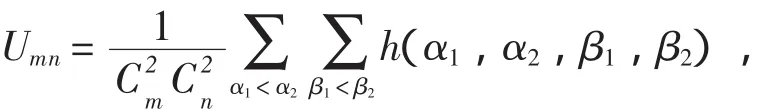
显然,将Umn化简后有

将h1(α1,α2),h2(β1,β2)的表达式代入推导可得:

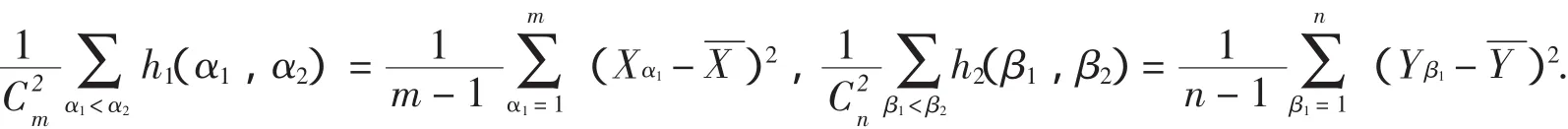
2 Umn的期望和方差

首先,由Umn化简后的表达式有EUmn=ESX2-ESY2=σ21-σ22,下面着重计算Umn的方差.

由于两样本是相互独立的,所以有

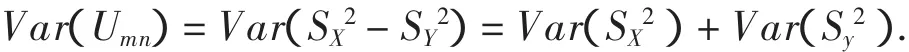
由文献[2]中的推导,可以得到如下两个结论:

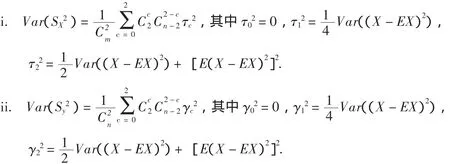
3 Umn的大样本性质

定理1[1]令m+n=N,若→λ,则当N→+∞时有

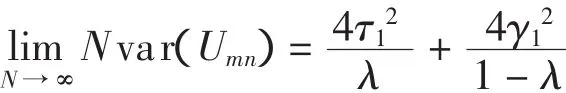
定理2[1]若Eh(α1,α2,β1,β2)2<∞,当时,有

在进行假设检验时,因为τ12,γ12的取值与总体分布有关,因此在大多数情况下,是未知的,因此需要找到它的估计量.

根据文献[2]的推论有如下两个结论:

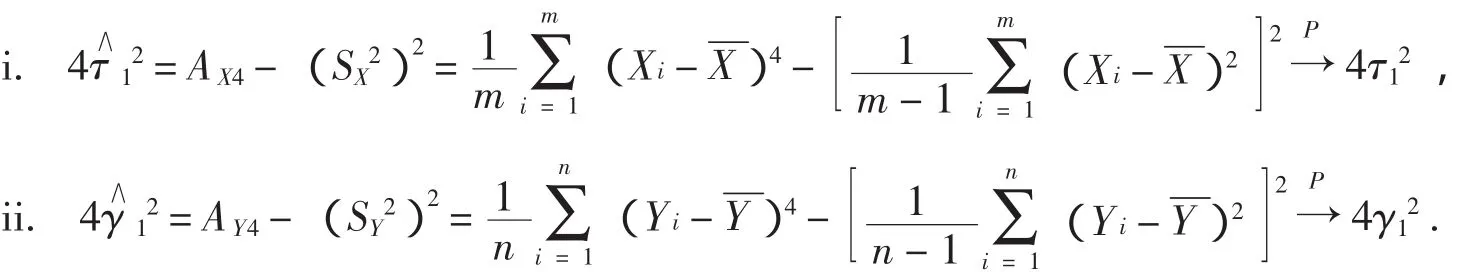
由大数定律得到

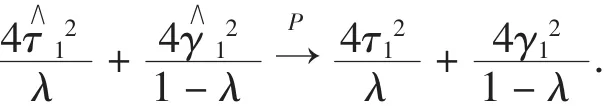
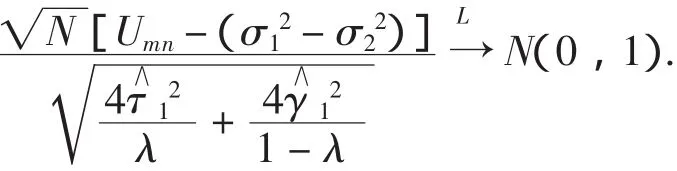
5 假设检验

假设问题H0:σ21=σ22,H1:σ21>σ22可等价变形为

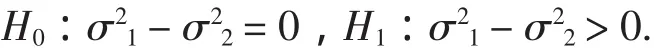
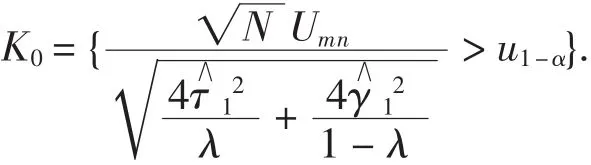
6 两种检验的功效

检验的功效指的是在备择假设成立时拒绝原假设的概率.比较两种检验方法的功效,可以比较给定显著性水平下,使两种检验方法达到相同的功效时所需的样本容量,所需样本容量越多,功效越低.

6.1 U统计量检验的功效

若假设θ=σ12-σ22,则原假设和备择假设可变为H0:θ=0,H1:θ>0

计算功效的参数θ与样本容量有关,且样本容量越大,计算功效的参数与原假设越接近,因此,取一个参数序列θ1≥θ2≥…≥θN≥…>0,假设m+n=N,m=λN,n=(1-λ)N.

下面计算检验在参数θN处达到功效β时所需的样本容量NU.

先计算备择假设成立时的概率值

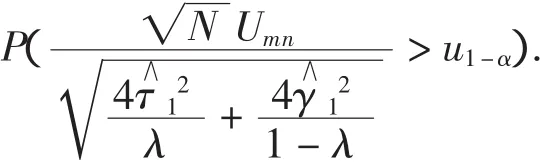
可得

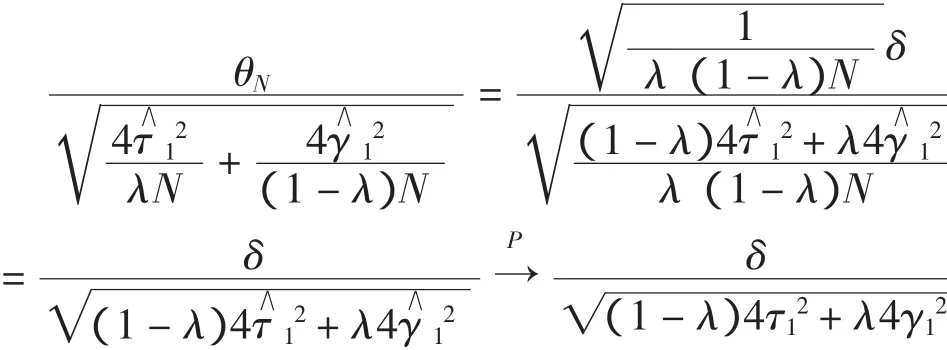
所以,由Slutsky[5]定理,备择假设成立时,有

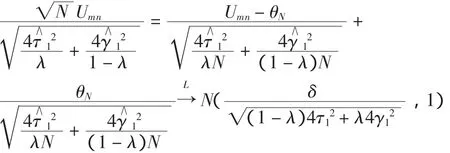
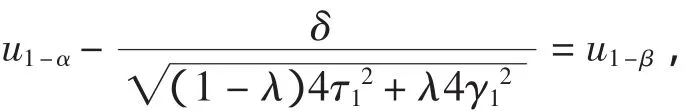
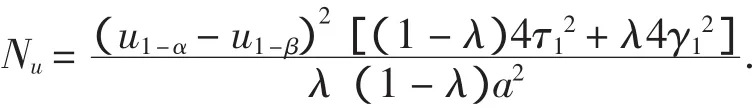
当总体为正态分布时,

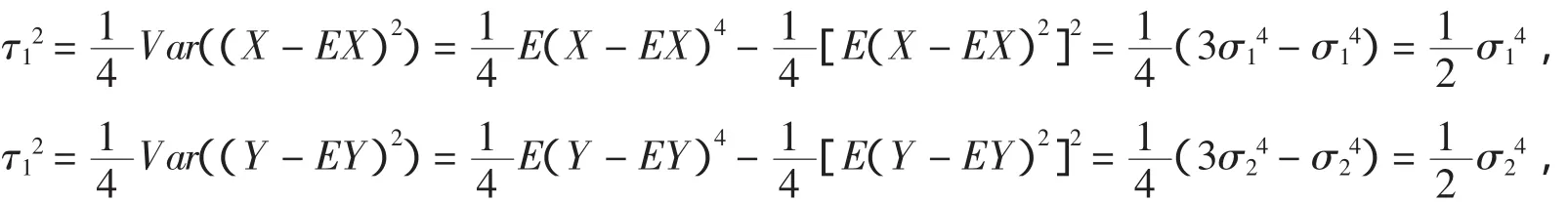
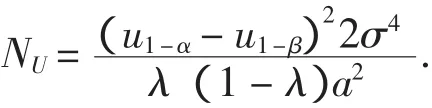
6.2 F检验的功效

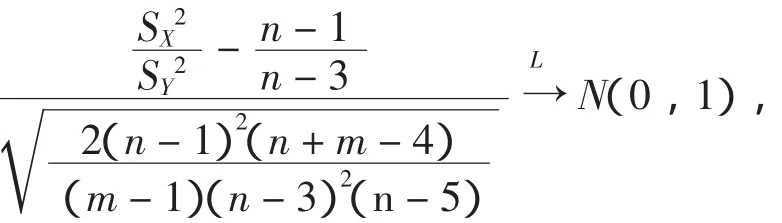
下面计算在参数α处达到功效β时所需的样本容量.

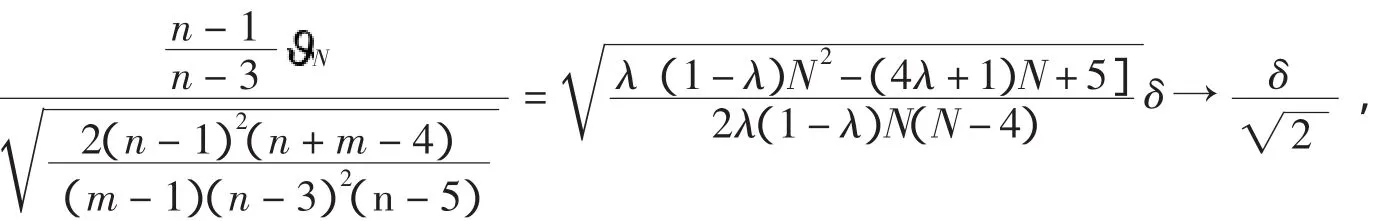
由Slutsky[5]定理有

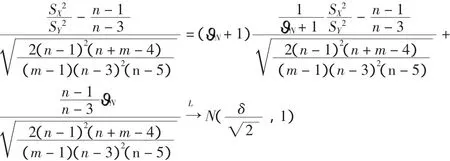
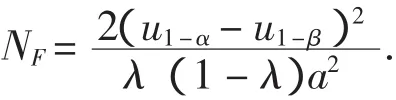
7 结论

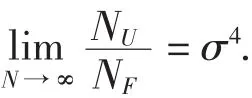
由计算结果可以看出,当σ2=1,检验的相对效率为1,即两种检验的功效相当.当两总体方差均小于1且总体4阶矩存在时,U统计量检验优于F统计量的检验,且适合于更加宽泛的场合,因此它是一种检验两个总体方差差异的实用方法.

综合6.1和6.2的结果,可以得到U统计量与F统计量检验的功效比率为

[1]孙山泽.非参数统计讲义[M].北京:北京大学出版社,2007:34-40.

[2]陆媛媛.单个总体方差差异的U统计量检验法[J].吉林大学学报:理学版,2011,49(6):1064-1067.

[3]宋立新.两总体分布均值相等的U统计量检验法[J].吉林大学学报:理学版,2011,48(6):957-960.

[4]李开灿.x2分布,t分布和F分布的一致渐近正态性[J].北京印刷学院学报,2004,12(3):30-33.

[5]陈希孺.数理统计引论[M].北京:科学出版社,2007:569-571.

[6]王静龙,梁小筠.非参数统计分析[M].北京:高等教育出版社,2006:154-155.